Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 2
21 câu hỏi
Nếu \(a.d = b.c\) và \(a,b,c,d\) đều khác \(0\) thì tỉ lệ thức nào sau đây là sai?
\(\frac{a}{c} = \frac{b}{d}.\)
\(\frac{a}{b} = \frac{c}{d}.\)
\(\frac{d}{b} = \frac{c}{a}.\)
\(\frac{c}{b} = \frac{d}{a}.\)
Gọi số đo ba góc của một tam giác là \(a,b,c\) tỉ lệ với \(2;3;4\). Khi đó, ta có dãy tỉ số bằng nhau là
\(\frac{a}{2} = \frac{b}{4} = \frac{c}{3}.\)
\(\frac{a}{2} = \frac{b}{3} = \frac{c}{4}.\)
\(\frac{a}{4} = \frac{b}{3} = \frac{c}{2}.\)
\(\frac{a}{4} = \frac{b}{2} = \frac{c}{3}.\)
Biết đại lượng \(y\) tỉ lệ thuận với đại lượng \(x\) theo hệ số \( - 2\). Biểu diễn \(y\) theo \(x\) là
\(y = \frac{1}{2}x.\)
\(y = - 2x.\)
\(x = - 2y.\)
\(y = 2x.\)
Cho bảng dưới đây biết \(x\) và \(y\) là hai đại lượng tỉ lệ nghịch.
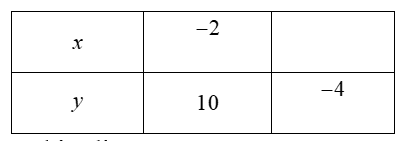
Giá trị ở ô trống trong bảng là
\( - 5.\)
\(0,8.\)
\( - 0,8.\)
\(5.\)
Biểu thức đại số biểu thị tích của hai số tự nhiên liên tiếp là
\(xy\) với \(x,y \in \mathbb{N}\).
\(x\left( {x + 1} \right)\) với \(x \in \mathbb{N}\).
\(x\left( {y + 1} \right)\) với \(x,y \in \mathbb{N}\).
\(\left( {x + 1} \right)\left( {y + 1} \right)\) với \(x,y \in \mathbb{N}\).
Trong các biểu thức sau, biểu thức nào là biểu thức số?
\(1,75 + \frac{1}{4}.24 + {2^3}.\)
\(2x - {3^2}.\)
\(25 - {3^2}.6x - {2^2}.\)
\(15 + x + \frac{1}{2}y\).
Biểu thức nào sau đây là đa thức một biến?
\( - {y^2} + 3y + 5.\)
\(2{y^3} - 3{x^2} + 5.\)
\( - y + 3x - 1.\)
\(x - 2xy + 5\).
Hệ số tự do của đa thức \({x^2} + \frac{3}{5}x - 7\) là
\( - 7.\)
\(1.\)
\(\frac{3}{5}.\)
\(7.\)
Ba cạnh của tam giác có độ dài là \({\rm{6 cm, 7 cm, 8 cm}}\) thì góc lớn nhất là góc
đối diện với cạnh có độ dài \({\rm{6 cm}}{\rm{.}}\)
đối diện với cạnh có độ dài \({\rm{7 cm}}{\rm{.}}\)
đối diện với cạnh có độ dài \({\rm{8 cm}}{\rm{.}}\)
ba góc có số đo bằng nhau.
Cho tam giác \(ABC\) có \(\widehat B = 70^\circ ;\widehat A = 50^\circ \). Em hãy chọn câu trả lời đúng nhất.
\(BC < AB < AC.\)
\(AC < AB < BC.\)
\(AC < BC < AB.\)
\(AB < BC < AC.\)
Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ dài của ba cạnh của một tam giác?
\(3{\rm{ cm, 5 cm, 2 cm}}{\rm{.}}\)
\({\rm{13 cm, 5 cm, 21 cm}}{\rm{.}}\)
\({\rm{9 cm, 6 cm, 3 cm}}{\rm{.}}\)
\({\rm{4 cm, 7 cm, 9 cm}}{\rm{.}}\)
Cho \(\Delta ABC\) có \(AM,BN\) là hai đường trung tuyến, \(G\) là trọng tâm. Nhận định nào sau đây là đúng?
\(AG = 2GM.\)
\(GM = 2AM.\)
\(AG = BG.\)
\(BG = 6BN.\)
Cô Ánh mua \(54\) hộp bánh gồm ba loại: loại \(I,\) loại \(II,\) loại \(III\). Loại \(I\) giá \(60\) nghìn đồng một hộp, loại \(II\) giá \(40\) nghìn đồng một hộp, loại \(III\) giá \(30\) nghìn đồng một hộp. Biết rằng số tiền cô Ánh mua ba loại bánh trên là như nhau. Gọi \(x,y,z\) lần lượt là số hộp bánh cô Ánh mua loại \(I,\) loại \(II,\) loại \(III\).
a) Điều kiện của \(x,y,z\) là \(x,y,z \in {\mathbb{N}^*}\) và \(x,y,z < 54.\)
b) Phương trình biểu diễn số hộp bánh cô Ánh mua là \(x + y + z = 54\).
c) Vì số tiền cô Ánh mua mỗi loại bánh là như nhau nên ta có tỉ lệ thức \(60x = 40y = 30z\).
d) Số hộp bánh loại \(III\) cô Ánh mua gấp hai lần số hộp bánh loại \(I.\)
Cho \(\Delta ABC\), kẻ \(AH \bot BC\) tại \(H.\) Kẻ \(BK \bot AC\) tại \(K\), \(CL \bot AB\) tại \(L.\)
a) \(AH < AB\).
b) \(2AH < AB + AC.\)
c) \(CL > \frac{1}{2}\left( {AC + CB} \right)\).
d) \(AH + BK + CL < AB + BC + CA.\)
Biết rằng \(\frac{x}{2} = \frac{y}{5}\) và \(2x - y = 3\). Tính giá trị của biểu thức \(A = x.y\).
Cứ \({\rm{100 kg}}\) thóc cho \(65{\rm{ kg}}\) gạo. Từ \({\rm{1 kg}}\) gạo người ta làm được \({\rm{2,2 kg}}\) bún tươi. Hỏi để làm ra \({\rm{14,3 kg}}\) bún tươi cần bao nhiêu kilôgram thóc?
Cho đa thức \(P\left( x \right) = {x^3} - 2{x^4} + 6x + 3 - 2x + 5\). Tính \(P\left( { - \frac{1}{2}} \right) - P\left( { - 1} \right)\).
(Kết quả ghi dưới dạng số thập phân)
Cho hình thang \(ABCD\) như hình vẽ dưới đây có \(AB = 7{\rm{ cm}}{\rm{.}}\) Gọi \(E\) là hình chiếu của \(B\) lên cạnh \(CD\). Biết \(ABED\) là hình vuông và diện tích hình thang \(ABCD\) gấp hai lần diện tích hình vuông \(ABED\).
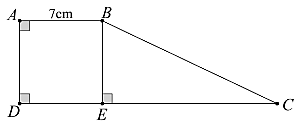
Hỏi khoảng cách từ \(C\) đến đường thẳng \(BE\) là bao nhiêu centimét?
(1,0 điểm) Ba bạn An, Bình, Cầm có số kẹo của An, Bình , Cầm tương ứng tỉ lệ với \(2;3;4\). Tính số kẹo của mỗi bạn, biết rằng Cầm nhiều hơn An \(8\) viên kẹo.
(1,0 điểm) Cho \(\Delta ABC\) có \(D\) là trung điểm của \(AC.\) Trên đoạn \(BD\) lấy điểm \(E\) sao cho \(BE = 2ED.\) Điểm \(F\) thuộc tia đối của tia \(DE\) sao cho \(BF = 2BE\). Gọi \(K\) là trung điểm của \(CF\) và \(G\) là giao điểm của \(EK\) và \(AC.\)
a) Chứng minh rằng \(G\) là trọng tâm tam giác \(EFC\).
b) Tính các tỉ số \(\frac{{GE}}{{GK}};\frac{{GC}}{{DC}}.\)
(1,0 điểm) Cho \(F\left( x \right) = 5{x^2} - 1 + 3x + {x^2} - 5{x^3}\) và \(G\left( x \right) = 2 - 3{x^3} + 6{x^2} + 5x - 2{x^3} - x\).
a) Thu gọn đa thức \(F\left( x \right),G\left( x \right)\) và tính \(F\left( x \right) - G\left( x \right)\).
b) Tìm đa thức \(N\left( x \right)\), biết rằng \(N\left( x \right) + F\left( x \right) = - G\left( x \right)\).








