Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
21 câu hỏi
Nếu \(\frac{a}{b} = \frac{c}{d}\) thì
\(a.d = b.c.\)
\(a.c = b.d.\)
\(a.b = c.d.\)
\(a = c.\)
Từ dãy tỉ số \(\frac{a}{5} = \frac{b}{3} = \frac{c}{7}\), ta có thể viết:
\(a:3 = b:5 = c:7.\)
\(a:5 = b:3 = c:7.\)
\(a:7 = b:5 = c:3.\)
\(a:3 = b:7 = c:5.\)
Theo thống kê, nếu dùng \(8\) xe chở hàng thì tiêu thụ hết \(70\) lít xăng. Vậy khi dùng \(13\) xe chở hàng cùng loại thì tiêu thụ hết bao nhiêu lít xăng?
\(113,75\) lít.
\(225,5\) lít.
\(728\) lít.
\(43,1\) lít.
Biết đại lượng \(y\) tỉ lệ nghịch với đại lượng \(x\) theo hệ số tỉ lệ là \( - 4\). Biểu diễn \(y\) theo \(x\) là
\(y = \frac{1}{4}x.\)
\(y = - 4x.\)
\(x = - 4y.\)
\(y = \frac{{ - 4}}{x}.\)
Trong các biểu thức sau, biểu thức số là
\(15 - x + y.\)
\(2 - \left( {3.4 + 5} \right).\)
\(3x - 2.\)
\(3x - \frac{y}{2} + 1.\)
Biểu thức biểu thị số tiền An phải trả để mua \(x\) quyển sách với giá \(10{\rm{ }}000\) đồng là
\(10{\rm{ }}000x.\)
\(x + 10{\rm{ 000}}{\rm{.}}\)
\(\frac{{10{\rm{ 000}}}}{x}.\)
\(\frac{x}{{10{\rm{ 000}}}}.\)
Biểu thức nào sau đây là đa thức một biến?
\(2{x^2} + 3y + 5.\)
\(2{x^3} - {x^2} + 5.\)
\(5xy + {x^3} - 1.\)
\(xyz - 2xy + 5.\)
Bậc của đa thức \(5{x^7} + 7{x^5} + {x^3} - 1\) là
\(5.\)
\(7.\)
\(3.\)
\(2.\)
Cho tam giác \(MNP\) có \(MN < MP < NP\). Tìm khẳng định đúng trong các khẳng định sau:
\(\widehat M < \widehat P < \widehat {N.}\)
\(\widehat N < \widehat P < \widehat {M.}\)
\(\widehat P < \widehat N < \widehat {M.}\)
\(\widehat P < \widehat M < \widehat {N.}\)
Chọn cụm từ thích hợp điền vào chỗ trống: “Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào có hình chiếu nhỏ hơn thì …”
lớn hơn.
ngắn nhất.
nhỏ hơn.
bằng nhau.
Bộ ba độ dài nào sau đây là độ dài của ba cạnh của một tam giác?
\(1{\rm{ cm, 2 cm, 3 cm}}{\rm{.}}\)
\(1{\rm{ cm, 3 cm, 5 cm}}{\rm{.}}\)
\({\rm{3 cm, 4 cm, 5 cm}}{\rm{.}}\)
\({\rm{2 cm, 4 cm, 6 cm}}{\rm{.}}\)
Giao điểm của ba đường trung tuyến trong một tam giác là
Trọng tâm của tam giác đó.
Điểm luôn thuộc một cạnh của tam giác đó.
Điểm cách đều ba đỉnh của tam giác đó.
Điểm cách đều ba cạnh của tam giác đó.
Bác An mua \(74\) chiếc bút bi gồm ba loại. Loại \(I\) giá \(6\) nghìn đồng một bút, loại \(II\) giá \(5\) nghìn đồng một bút, loại \(III\) giá \(4\) nghìn đồng một bút. Biết rằng số tiền bác An mua mỗi loại bút là như nhau. Gọi \(x,y,z\) lần lượt là số bút bi bác An mua loại \(I,\) \(II\), \(III\).
a) Điều kiện của \(x,y,z\) là \(x,y,z \in {\mathbb{N}^*}\) và \(x,y,z < 74.\)
b) Phương trình biểu diễn số bút bác An mua là \(x + y + z = 74\).
c) Vì số tiền bác An mua mỗi loại bút là như nhau nên ta có tỉ lệ thức \(\frac{x}{6} = \frac{y}{5} = \frac{z}{4}.\)
d) Số bút loại \(I\) nhiều hơn số bút loại \(II\) là \(4\) chiếc.
Cho hình vẽ sau:
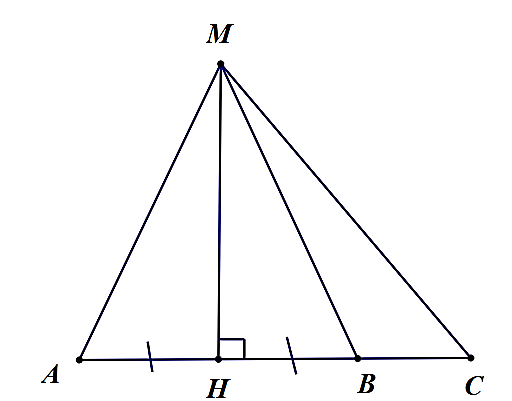
Xét tính đúng – sai trong các mệnh đề dưới đây:
a) \(MA > MH.\)
b) \(MC > MB.\)
c) \(MA = MB.\)
d) \(MC < MA.\)
Biết tỉ số giữa chiều dài và chiều rộng của hình chữ nhật đó là \(\frac{3}{2}\) và chu vi hình chữ nhật là \(20{\rm{ cm}}\). Hỏi chiều dài của hình chữ nhật đó là bao nhiêu centimet?
Biết độ dài ba cạnh của một tam giác tỉ lệ với các số \(3;5;7\) và chu vi của tam giác đó là \(45{\rm{ cm}}{\rm{.}}\) Hỏi độ dài cạnh lớn nhất của tam giác đó là bao nhiêu centimet?
Cho đa thức \(P\left( x \right) = 2{x^3} + {x^2} + 5 - 3x + 3{x^2} - 2{x^3} - 4{x^2} + 1\). Tính giá trị của biểu thức \(P\left( 0 \right) - P\left( { - 1} \right)\).
Cho hình vẽ bên, biết \(AB = DC\), \(\widehat {BAC} = \widehat {BDC} = 90^\circ \) và \(ED = 4{\rm{ cm}}\). Hỏi khoảng cách từ \(E\) đến đường thẳng \(AB\) là bao nhiêu centimet?
(1,0 điểm) Ba tấm vải dài tổng cộng \(210{\rm{ m}}{\rm{.}}\) Sau khi bán đi \(\frac{1}{7}\) tấm vải thứ nhất, \(\frac{2}{{11}}\) tấm vải thứ hai và \(\frac{1}{3}\) tấm vải thứ ba thì chiều dài còn lại của ba tấm vải là bằng nhau. Hỏi mỗi tấm vải ban đầu dài bao nhiêu mét?
(1,0 điểm) Cho \(\Delta ABC\) cân tại \(A\) có hai đường trung tuyến \(BD\) và \(CE\) cắt nhau tại \(G\). Biết \(BD = CE\).
a) Chứng minh tam giác \(GBC\) là tam giác cân.
b) Chứng minh \(DG + EG > \frac{1}{2}BC\).
(1,0 điểm) Cho hai đa thức \(f\left( x \right) = {x^2} - 2x - 5{x^4} + 6\) và \(g\left( x \right) = {x^3} - 5{x^4} + 3{x^2} - 3.\)
a) Tính \(f\left( x \right) + g\left( x \right)\) và sắp xếp đa thức theo lũy thừa giảm dần của biến.
c) Tìm đa thức \(h\left( x \right)\), biết rằng \(h\left( x \right) + f\left( x \right) - g\left( x \right) = - 2{x^3} - x + 9.\)








