Bộ 10 đề thi giữa kì 2 Toán 12 Chân trời sáng tạo cấu trúc mới có đáp án (Đề 7)
22 câu hỏi
Cho hàm số \(f\left( x \right) = 3{x^2} + 2x\). Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của \(f\left( x \right)\) trên \(\mathbb{R}\).
\({F_1}\left( x \right) = {x^3} + {x^2} - 4\).
\({F_2}\left( x \right) = \frac{{{x^3}}}{3} + \frac{{{x^2}}}{2}\).
\({F_3}\left( x \right) = {x^3} - {x^2} + 1\).
\[{F_4}\left( x \right) = 3{x^3} + {x^2}\].
Mệnh đề nào dưới đây đúng?
\(\int\limits_1^2 {\frac{1}{{{e^x}}}} dx = \left. {\frac{1}{{{e^x}}}} \right|_1^2\).
\(\int\limits_1^2 {\frac{1}{{{e^x}}}} dx = \left. {{e^x}} \right|_1^2\).
\(\int\limits_1^2 {\frac{1}{{{e^x}}}} dx = \left. {{e^x}} \right|_2^1\).
\[\int\limits_1^2 {\frac{1}{{{e^x}}}} dx = \left. {\frac{1}{{{e^x}}}} \right|_2^1\].
Cho \(\int\limits_1^2 {f\left( x \right)dx} = \frac{1}{2},\int\limits_3^4 {f\left( x \right)dx} = \frac{3}{4}\). Kết quả \(\int\limits_1^4 {f\left( x \right)dx} - \int\limits_2^3 {f\left( x \right)dx} \) bằng
\(\frac{3}{8}\).
\(\frac{5}{4}\).
\(\frac{5}{8}\).
\(\frac{1}{4}\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\). Gọi \(D\) là diện tích hình phẳng giới hạn bởi đồ thị \(\left( C \right):y = f\left( x \right)\), trục hoành, hai đường thẳng \(x = - 2;x = 4\) (tham khảo hình vẽ bên dưới).
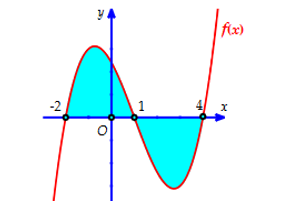
Giả sử \({S_D}\) là diện tích hình phẳng \(D\). Mệnh đề nào dưới đây sai?
\({S_D} = \int\limits_{ - 2}^4 {\left| {f\left( x \right)} \right|dx} \).
\({S_D} = \left| {\int\limits_{ - 2}^4 {f\left( x \right)dx} } \right|\).
\({S_D} = \left| {\int\limits_{ - 2}^1 {f\left( x \right)dx} } \right| + \left| {\int\limits_1^4 {f\left( x \right)dx} } \right|\).
\({S_D} = \int\limits_{ - 2}^1 {f\left( x \right)dx} - \int\limits_1^4 {f\left( x \right)dx} \).
Tính \(I = \int\limits_0^2 {\frac{2}{{2x + 1}}dx} \).
\(I = \frac{1}{2}\ln 5\).
\(\ln 5\).
\(I = 4\ln 5\).
\(I = 2\ln 5\).
Cho vật thể \(\left( T \right)\) được giới hạn bởi hai mặt phẳng \(x = - 2;x = 2\). Biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\)(\( - 2 \le x \le 2\)) là một hình vuông có cạnh bằng \(\sqrt {4 - {x^2}} \). Thể tích vật thể \(\left( T \right)\) bằng.
\(\pi \).
\(\frac{{32}}{3}\).
\(\frac{{32\pi }}{3}\).
\(\frac{8}{3}\).
Trong không gian \(Oxyz\) cho mặt phẳng \(\left( P \right):x + 2y + 3z - 5 = 0\) có một vectơ pháp tuyến là
\(\overrightarrow {{n_3}} = \left( { - 1;2;3} \right)\).
\(\overrightarrow {{n_4}} = \left( {1;2; - 3} \right)\).
\(\overrightarrow {{n_2}} = \left( {1;2;3} \right)\).
\(\overrightarrow {{n_1}} = \left( {3;2;1} \right)\).
Trong không gian \(Oxyz\), mặt phẳng \(\left( P \right):\frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 1\) không đi qua điểm nào dưới đây:
\(P\left( {0;2;0} \right)\).
\(Q\left( {0;0;3} \right)\).
\(M\left( {1;2;3} \right)\).
\(N\left( {1;0;0} \right)\).
Trong không gian \(Oxyz\), phương trình mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(A\left( {2; - 1;3} \right)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {2;3; - 1} \right)\) là
\(\left( \alpha \right):2x + 3y - z - 2 = 0\).
\(\left( \alpha \right):2x + 3y - z + 2 = 0\).
\(\left( \alpha \right):2x - y + 3z - 2 = 0\).
\(\left( \alpha \right):2x - y + 3z + 2 = 0\).
Trong không gian \(Oxyz\), vectơ nào sau đây là một vectơ pháp tuyến của \(\left( P \right)\), biết \(\overrightarrow a = \left( { - 1; - 2; - 2} \right),\overrightarrow b = \left( { - 1;0; - 1} \right)\) là cặp vectơ chỉ phương của \(\left( P \right)\)?
\(\overrightarrow n = \left( {2;1;2} \right)\).
\(\overrightarrow n = \left( {2; - 1; - 2} \right)\).
\(\overrightarrow n = \left( {2;1; - 2} \right)\).
\(\overrightarrow n = \left( { - 2;1; - 2} \right)\).
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):2x - 2y + z - 1 = 0\). Khoảng cách từ điểm \(M\left( { - 1;2;0} \right)\) đến mặt phẳng \(\left( P \right)\) bằng
\(5\).
\(2\).
\(\frac{5}{3}\).
\(\frac{4}{3}\).
Trong không gian \(Oxyz\), cho điểm \(A\left( {2; - 1; - 3} \right)\) và mặt phẳng \(\left( P \right):3x - 2y + 4z - 5 = 0\). Mặt phẳng \(\left( Q \right)\) đi qua \(A\) và song song với mặt phẳng \(\left( P \right)\) có phương trình:
\(\left( Q \right):3x - 2y + 4z - 4 = 0\).
\(\left( Q \right):3x - 2y + 4z + 4 = 0\).
\(\left( Q \right):3x - 2y + 4z + 5 = 0\).
\(\left( \alpha \right):3x + 2y + 4z + 8 = 0\).
Cho hàm số \(f\left( x \right) = 2x + {e^x}\). Biết \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\) thỏa mãn \(F\left( 0 \right) = 2025\).
a) \(f\left( 2 \right) = 4 + e\).
b) \(\int {f\left( x \right)dx} = \int {\left( {2x + {e^x}} \right)dx} = {x^2} + {e^x} + C\).
c) \(F\left( x \right) = {x^2} + {e^x} + 2024\).
d) \(\int {xf'\left( {{x^2}} \right)dx} = \int {x\left( {2 + {e^{{x^2}}}} \right)dx = {x^2} + x{e^{{x^2}}} + C} \).
Cho hàm số \(f\left( x \right)\) liên tục và không âm trên đoạn \(\left[ {0;3} \right]\). \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) trên đoạn \(\left[ {0;3} \right]\) thỏa mãn \(F\left( 3 \right) = 2;F\left( 0 \right) = 1\).
a) Hiệu số \(F\left( 3 \right) - F\left( 0 \right)\) gọi là tích phân từ 3 đến 0 của hàm số \(f\left( x \right)\).
b)\(\int\limits_0^3 {f\left( x \right)} dx = - \int\limits_3^0 {f\left( x \right)} dx = F\left( 3 \right) - F\left( 0 \right)\).
c) \(\int\limits_0^3 {f\left( t \right)} dt = 1\).
d) Hình thang cong giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = 0;x = 3\) có diện tích bằng 1.
Cho \(y = f\left( x \right)\) là hàm số bậc hai có đồ thị \(\left( P \right)\) như hình vẽ bên. Gọi \(\left( H \right)\) là hình phẳng giới hạn bởi \(\left( P \right)\) với trục hoành.
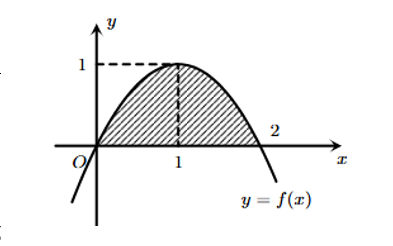
a) Hoành độ giao điểm của parabol với trục hoành là \(x = 1\) và \(x = 2\).
b) Phương trình của parabol là \(y = 2x - {x^2}\).
c) Diện tích của hình \(\left( H \right)\) bằng \(\frac{2}{3}\).
d) Khi cho hình \(\left( H \right)\) xoay quanh trục \(Ox\) ta được một vật thể có thể tích bằng \(\frac{{16}}{{15}}\).
Trong không gian \(Oxyz\) cho hai điểm \(A\left( {2;3;7} \right),B\left( {4;1;3} \right)\). Gọi \(\left( \alpha \right)\) là mặt phẳng trung trực của đoạn thẳng \(AB\). Gọi \(I\) là trung điểm của \(AB\).
a) Mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(I\left( {1; - 1; - 2} \right)\).
b) Mặt phẳng \(\left( \alpha \right)\) có vectơ pháp tuyến là \(\overrightarrow n \left( { - 1;1;2} \right)\).
c) Phương trình mặt phẳng \(\left( \alpha \right)\) có dạng \(ax + by + cz - 9 = 0\). Khi đó \(a + b + c = 2\).
d) Khoảng cách từ \(C\left( {0; - 1;2} \right)\) đến mặt phẳng \(\left( \alpha \right)\) là \(\frac{{\sqrt 6 }}{6}\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm là \(f'\left( x \right) = \sin 2x,\forall x \in \mathbb{R}\) và \(f\left( {\frac{\pi }{4}} \right) = 0\). Biết \(F\left( x \right)\) là nguyên hàm của \(f\left( x \right)\) thỏa mãn \(F\left( {\frac{\pi }{2}} \right) = 2\). Khi đó \(F\left( {\frac{\pi }{4}} \right)\) bằng bao nhiêu?
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}2x + a\;{\rm{khi}}\;x \ge 1\\3{x^2} + b\;{\rm{khi}}\;x < 1\end{array} \right.\) thỏa mãn \(\int\limits_0^2 {f\left( x \right)dx = 13} \). Tính \(a + b - ab\).
Một đám vi trùng ngày thứ t có số lượng là \(N\left( t \right)\). Biết rằng \(N'\left( t \right) = \frac{4}{{1 + 0,5t}}\) và lúc đầu đám vi trùng có 250 con. Sau 10 ngày số lượng vi trùng là bao nhiêu con? (kết quả làm tròn đến hàng đơn vị).
Tốc độ chuyển động \(v\left( {{\rm{m/s}}} \right)\) của ca nô trong khoảng thời gian 40 giây được thể hiện như hình bên dưới
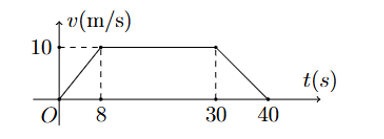
Quãng đường đi được (tính bằng m) của ca nô trong khoảng thời gian này là bao nhiêu?
Trong không gian \(Oxyz\), cho \(A\left( {1;1;0} \right),B\left( {0;2;1} \right),C\left( {1;0;2} \right),D\left( {1;1;1} \right)\). Mặt phẳng \(\left( \alpha \right):ax + by + z + c = 0\) là mặt phẳng đi qua \(A\left( {1;1;0} \right),B\left( {0;2;1} \right)\) và song song với đường thẳng \(CD\). Tính \(a + b + c\).
Cho tứ diện \[OABC\], có \[OA,OB,OC\]đôi một vuông góc và \[OA = 5,OB = 2,OC = 4\]. Gọi \[M,N\] lần lượt là trung điểm của \[OB\]và \[OC\]. Gọi \[G\] là trọng tâm của tam giác \[ABC\]. Tính khoảng cách từ \[G\] đến mặt phẳng \[\left( {AMN} \right)\] (kết quả làm tròn đến hàng phần trăm).








