Bộ 10 đề thi giữa kì 2 Toán 12 Chân trời sáng tạo cấu trúc mới có đáp án (Đề 4)
22 câu hỏi
Cho các hàm số \(f\left( x \right),g\left( x \right)\) có đạo hàm trên \(K\). Mệnh đề nào dưới đây sai?
\(\int {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} = \int {f\left( x \right)dx} + \int {g\left( x \right)dx} \).
\(\int {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} = \int {f\left( x \right)dx} - \int {g\left( x \right)dx} \).
\(\int {g\left( x \right)dx} = g'\left( x \right) + C\).
\(\int {f'\left( x \right)dx} = f\left( x \right) + C\).
Nếu \(\int\limits_0^9 {f\left( x \right)dx} = 37\) và \(\int\limits_0^9 {g\left( x \right)dx} = 16\) thì \(\int\limits_0^9 {\left[ {2f\left( x \right) + 3g\left( x \right)} \right]dx} \) bằng
\(122\).
\(74\).
\(48\).
\(53\).
Nếu \(\int\limits_a^d {f\left( x \right)dx} = 5,\int\limits_b^d {f\left( x \right)dx} = 2\) với \(a < d < b\) thì \(\int\limits_a^b {f\left( x \right)dx} \) có giá trị bằng:
\( - 2\).
\(3\).
\(8\).
\(0\).
Gọi \(S\) là diện tích hình phẳng giới hạn bởi các đường \(y = {3^x},y = 0,x = 0\) và \(x = 2\). Mệnh đề nào dưới đây là đúng?
\(S = \pi \int\limits_0^2 {{3^x}dx} \).
\(S = \int\limits_0^2 {{3^{2x}}dx} \).
\(S = \int\limits_0^2 {{3^x}dx} \).
\(S = \pi \int\limits_0^2 {{3^{2x}}dx} \).
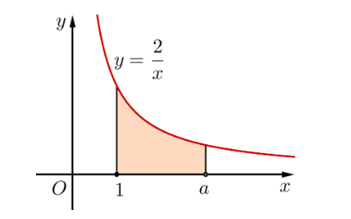
Tìm \(a\) để diện tích hình thang cong giới hạn bởi đồ thị \(\left( C \right):y = f\left( x \right) = \frac{2}{x},\) trục hoành và các đường thẳng \(x = 1,x = a\left( {a > 1} \right)\) bằng 2.
\({e^2}\).
\(e\).
\(2e\).
\(e + 1\).
Cho hàm số \(y = f\left( x \right) = \left\{ \begin{array}{l}3{x^2}\;{\rm{khi}}\;0 \le x \le 1\\4 - x\;{\rm{khi}}\;1 < x \le 2\end{array} \right.\). Tính tích phân \(\int\limits_0^2 {f\left( x \right)dx} \).
\(\frac{7}{2}\).
\(1\).
\(\frac{5}{2}\).
\(\frac{3}{2}\).
Trong không gian \(Oxyz\), cho mặt phẳng \((P):3x - y + 2z - 1 = 0\). Vectơ nào dưới đây không phải là một vectơ pháp tuyến của \((P)\)?
\(\overrightarrow n = ( - 3;1; - 2)\).
\(\overrightarrow n = (3;1;2)\).
\(\overrightarrow n = (3; - 1;2)\).
\(\overrightarrow n = (6; - 2;4)\).
Trong không gian \[Oxyz\], cho mặt phẳng \[\left( P \right):x + y + z - 3 = 0\]. Chọn mệnh đề sai?
Điểm\[M\left( { - 1; - 1; - 1} \right)\] không thuộc mặt phẳng \(\left( P \right)\).
Điểm\[N\left( {1;1;1} \right)\] thuộc mặt phẳng \(\left( P \right)\).
Điểm\(K\left( { - 3;0;0} \right)\) không thuộc mặt phẳng \(\left( P \right)\).
Điểm\(Q\left( {0;0; - 3} \right)\) thuộc mặt phẳng \(\left( P \right)\).
Khoảng cách từ điểm \[M\left( {3;\,\,2;\,\,1} \right)\] đến mặt phẳng (P): \(Ax + Cz + D = 0\), \(A.C.D \ne 0\). Chọn khẳng định đúng trong các khẳng định sau:
\(d(M,(P)) = \frac{{\left| {3A + C + D} \right|}}{{\sqrt {{A^2} + {C^2}} }}\).
\[d(M,(P)) = \frac{{\left| {A + 2B + 3C + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}.\]
\(d(M,(P)) = \frac{{\left| {3A + C} \right|}}{{\sqrt {{A^2} + {C^2}} }}.\)
\[d(M,(P)) = \frac{{\left| {3A + C + D} \right|}}{{\sqrt {{3^2} + {1^2}} }}.\]
Trong không gian \(Oxyz\), phương trình của mặt phẳng đi qua điểm \(A\left( {3;0; - 1} \right)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {4; - 2; - 3} \right)\) là
\(4x - 2y + 3z - 9 = 0\).
\(4x - 2y - 3z - 15 = 0\).
\(3x - z - 15 = 0\).
\(4x - 2y - 3z + 15 = 0\).
Trong không gian \(Oxyz\), khoảng cách giữa hai mặt phẳng \(\left( P \right):x + 2y + 2z - 10 = 0\) và \(\left( Q \right):x + 2y + 2z - 3 = 0\)bằng:
\(\frac{4}{3}\)
\(\frac{8}{3}\).
\(\frac{7}{3}\).
\(3\).
Trong không gian với hệ tọa độ \(Oxyz\), cặp vectơ \(\overrightarrow a = \left( {2;1; - 2} \right),\overrightarrow b = \left( {1;0;2} \right)\) có giá song song với mặt phẳng \(\left( P \right)\). Phương trình mặt phẳng \(\left( P \right)\)qua \(C\left( {1;1;3} \right)\) là
\(2x + 6y - z - 7 = 0\).
\(2x - 6y - z + 5 = 0\).
\(2x + 6y + z + 5 = 0\).
\(2x - 6y - z + 7 = 0\).
Cho các hàm số \(f\left( x \right) = 2\cos \left( {\frac{\pi }{2} + x} \right) - 3{x^2}\) và \(g\left( x \right) = 2\sin x\).
a) \(f\left( x \right) + g\left( x \right) = 4\sin x - 3{x^2}\).
b)\(f'\left( x \right) = - 2\cos x - 6x\).
c) \(\int {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} = - {x^3} + C\).
d) \(\int {g\left( x \right)dx + g'\left( x \right)} = 0\).
Cho hàm số \(f\left( x \right) = {e^x}\left( {x + 1} \right)\).
a)\(F\left( x \right) = x{e^x}\) là một nguyên hàm của \(f\left( x \right)\).
b) \(\int\limits_1^2 {f\left( x \right)dx} = \left. {{e^x}\left( {\frac{{{x^2}}}{2} + x} \right)} \right|_1^2\).
c) Nếu \(\int\limits_{\ln 3}^{\ln 10} {f\left( x \right)dx} = a\ln a - b\ln b\) với \(a,b \in \mathbb{N}\) thì \(a + b = 7\).
d) Giá trị tích phân \(\int\limits_{ - 2}^2 {f\left( x \right)dx} \) là diện tích hình thang cong giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và các đường thẳng \(x = - 2;x = 2\).
Cho hình phẳng \(\left( H \right)\) giới hạn bởi đồ thị hàm số \(y = f\left( x \right) = \frac{{x + 1}}{x}\), trục hoành và hai đường thẳng \(x = 2,x = 6\). Khi đó
a) Diện tích hình phẳng \(\left( H \right)\) là \(s = 4 + \ln 3\).
b) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right) - 1\), trục hoành và hai đường thẳng \(x = 2;x = 6\) là \(S = 2\ln 3\).
c) Thể tích vật thể tròn xoay tạo thành khi quay \(\left( H \right)\) quanh trục \(Ox\) là \(V = \frac{{\left( {13 + 6\ln 3} \right)\pi }}{3}\).
d) Thể tích vật thể tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\) và các đường thẳng \(y = 1;x = 2;x = 6\) quanh trục \(Ox\) là \(V = \frac{{1 + 6\ln 3}}{3}\).
Trong không gian với hệ trục tọa độ \(Oxyz\), cho hai điểm \(A\left( {1;3;0} \right),B\left( {3;1;0} \right)\) và mặt phẳng \(\left( P \right):x - y + z + 5 = 0\).
a)\(\overrightarrow {AB} = \left( {2; - 2;0} \right)\).
b)\(A\left( {1;3;0} \right)\) cách mặt phẳng \(\left( {Oyz} \right)\) một khoảng bằng 1.
c) Điểm \(B\left( {3;1;0} \right)\) cách mặt phẳng \(\left( P \right):x - y + z + 5 = 0\) một khoảng bằng \(\frac{{7\sqrt 3 }}{3}\).
d) Mặt phẳng \(\left( Q \right)\) song song với mặt phẳng \(\left( P \right)\) và cách đều hai điểm \(A,B\) có dạng \(x + by + cz + d = 0\). Khi đó \(b + c + d = 5\).
Biết hàm số \(f\left( x \right) = {7^x}{.4^{2x}}\) có nguyên hàm \(F\left( x \right) = \frac{{{a^x}}}{{\ln a}} + C\) với \(a \in \mathbb{Z}\). Tìm \(a\).
Cho \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right) = \frac{{2{{\left( {3 - x} \right)}^2}}}{{{x^2}}}\) thỏa \(F\left( { - 1} \right) + F\left( 1 \right) = 6\). Khi đó giá trị biểu thức \(F\left( { - 2} \right) + F\left( 2 \right)\) có dạng \(a + b\ln 2\) với \(a,b \in \mathbb{Z}\). Tính \(T = ab\).
Một vật chuyển động với vận tốc tăng liên tục được biểu thị bằng đồ thị là đường cong parabol ở hình bên dưới
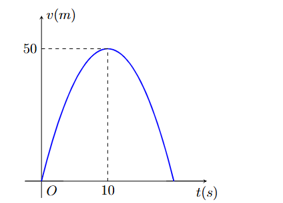
Biết rằng sau 10 giây thì vật đó đạt đến vận tốc cao nhất và bắt đầu giảm tốc. Hỏi từ lúc bắt đầu đến lúc đạt vận tốc cao nhất thì vật đó đi được quãng đường bao nhiêu mét (làm tròn đến chữ số hàng đơn vị).
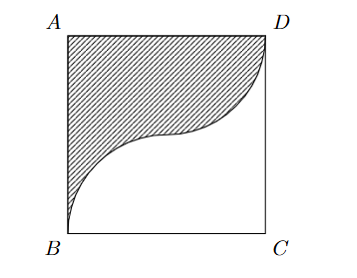
Một vật trang trí có dạng một khối tròn xoay được tạo thành khi xoay miền \(\left( R \right)\) (phần gạch chéo trong hình vẽ bên) quanh trục \(AB\). Miền \(\left( R \right)\) được giới hạn bởi các cạnh \(AB,AD\) của hình vuông \(ABCD\) và các cung phần tư của các đường tròn bán kính bằng 1 cm với tâm lần lượt là trung điểm của các cạnh \(BC,AD\). Tính thể tích của vật trang trí đó (đơn vị cm3), làm tròn kết quả đến hàng phần mười.
Trong không gian \(Oxyz\), phương trình mặt phẳng đi qua \(M\left( {3; - 1;2} \right),N\left( {4; - 1; - 1} \right),P\left( {2;0;2} \right)\) có dạng \(3x + By + Cz + D = 0\). Tính \({B^2} + {C^2} + {D^2}\).
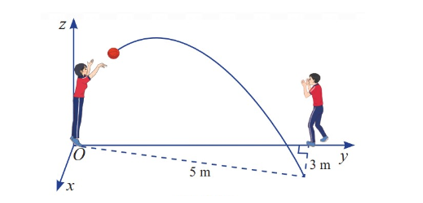
Hai học sinh đang chuyền bóng. Bạn nữ ném bóng cho bạn nam. Quả bóng bay trên không, lệch sang phải và rơi xuống tại vị trí cách bạn nam 3 m, cách bạn nữ 5 m. Cho biết quỹ đạo của quả bóng nằm trong mặt phẳng \(\left( P \right)\) vuông góc với mặt đất. Phương trình của \(\left( P \right)\) trong trong không gian \(Oxyz\) được mô tả như trong hình vẽ có dạng \(ax + 3y + cz + d = 0\). Giá trị của \(a + cd\) là bao nhiêu?