Bộ 10 đề thi giữa kì 2 Toán 12 Chân trời sáng tạo cấu trúc mới có đáp án (Đề 3)
22 câu hỏi
Cho \(\int {f\left( x \right)} \,{\rm{d}}x = - \cos x + C\). Khẳng định nào dưới đây đúng?
\(f\left( x \right) = - \sin x\).
\(f\left( x \right) = - \cos x\).
\(f\left( x \right) = \sin x\).
\(f\left( x \right) = \cos x\).
Cho hàm số \[y = f\left( x \right)\]liên tục trên \[\left[ {a;b} \right]\]. Mệnh đề nào đúng?
\[\int\limits_a^b {f\left( x \right){\rm{d}}x} = \int\limits_b^a {f\left( x \right){\rm{d}}x} \].
\[\int\limits_a^b {f\left( x \right){\rm{d}}x} = - \int\limits_b^a {f\left( x \right){\rm{d}}x} \].
\[\int\limits_a^b {f\left( x \right){\rm{d}}x = 2\int\limits_a^b {f\left( x \right){\rm{d}}\left( {2x} \right)} } \].
\[\int\limits_a^b {2024f\left( x \right){\rm{d}}x = 0} .\]
Biết \(F\left( x \right) = {x^2}\) là một nguyên hàm của hàm số \(f(x)\) trên \(\mathbb{R}\). Giá trị của \(\int\limits_1^3 {\left[ {1 + f(x)} \right]dx} \) bằng
\(10\).
\(8\).
\(\frac{{26}}{3}\).
\(\frac{{32}}{3}\).
Cho hình phẳng \(\left( H \right)\) giới hạn bởi các đường \(y = {x^2} + 3\), \(y = 0\), \(x = 0\), \(x = 2\). Gọi \(V\) là thể tích của khối tròn xoay được tạo thành khi quay \(\left( H \right)\) xung quanh trục \(Ox\). Mệnh đề nào dưới đây đúng?
\(V = \int\limits_0^2 {\left( {{x^2} + 3} \right)dx} \).
\(V = \pi \int\limits_0^2 {\left( {{x^2} + 3} \right)dx} \).
\(V = \int\limits_0^2 {{{\left( {{x^2} + 3} \right)}^2}dx} \).
\(V = \pi \int\limits_0^2 {{{\left( {{x^2} + 3} \right)}^2}dx} \).
Tích phân \(\int\limits_0^1 {\left( {3x + 1} \right)\left( {x + 3} \right){\rm{d}}x} \)bằng
\(12\).
\(9\).
\(5\).
\(6\).
Cắt một vật thể bởi hai mặt phẳng vuông góc với trục \[Ox\]tại \(x = 1\) và \(x = 2\). Một mặt phẳng tùy ý vuông góc với trục \[Ox\] tại điểm có hoành độ \(x\) (\(1 \le x \le 2\)) cắt vật thể đó có diện tích \(S\left( x \right) = 2024x\). Tính thể tích của phần vật thể giới hạn bởi hai mặt phẳng trên.
\(V = 3036\).
\(V = 3036\pi \).
\(V = 1518\).
\(V = 1518\pi \).
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):\,2x - y + z - 3 = 0\). Vectơ nào dưới đây là một véctơ pháp tuyến của mặt phẳng \(\left( P \right)\)?
\(\overrightarrow {{n_4}} = \left( { - 2;1;1} \right)\).
\(\overrightarrow {{n_3}} = \left( {2;1;1} \right)\).
\(\overrightarrow {{n_2}} = \left( {3; - 1; - 1} \right)\).
\(\overrightarrow {{n_1}} = \left( { - 2;1; - 1} \right)\).
Trong không gian \(Oxyz\), vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng \(\left( {Oxz} \right)\).
\(\vec j = \left( {0;\,1;\,0} \right)\).
\(\vec n = \left( {1;0;1} \right)\).
\(\vec i = \left( {1;0;0} \right)\).
\(\vec k = \left( {0;0;1} \right)\).
Trong không gian tọa độ \(Oxyz,\) cho mặt phẳng \(\left( \alpha \right):2x + 3y + 6z + 6 = 0.\) Điểm nào sau đây không thuộc mặt phẳng \(\left( \alpha \right)\)?
\(M\left( { - 3;0;0} \right)\).
\(N\left( {1; - 1;0} \right)\).
\(P\left( {0; - 2;0} \right)\).
\(Q\left( {0;0; - 1} \right)\).
Trong không gian với hệ trục tọa độ \[Oxyz\], cho hai điểm \[M\left( {1;2; - 4} \right)\] và \[M'\left( {5;4;2} \right)\]. Biết rằng \[M'\] là hình chiếu vuông góc của \[M\] lên mặt phẳng \[\left( \alpha \right)\], khi đó mặt phẳng \[\left( \alpha \right)\] có một vectơ pháp tuyến là
\[\overrightarrow n \left( {2; - 1;3} \right)\].
\[\overrightarrow n \left( {3;3; - 1} \right)\].
\[\overrightarrow n \left( {2;1;3} \right)\].
\[\overrightarrow n \left( {2;3;3} \right)\].
Trong không gian với hệ tọa độ \(Oxyz\), cho mặt phẳng \(\left( P \right):x + 2y + z - 6 = 0\). Chọn khẳng định sai trong các khẳng định sau?
Mặt phẳng \(\left( P \right)\) có vectơ pháp tuyến là \(\overrightarrow n = \left( {1\,;\,2\,;\,1} \right)\).
Mặt phẳng \(\left( P \right)\) đi qua điểm \(A\left( {3\,;\,4\,;\, - 5} \right)\).
Mặt phẳng \(\left( P \right)\) song song với mặt phẳng \(\left( Q \right):x + 2y + z + 5 = 0\).
Cho \(I\left( {1\,;\,7\,;\,3} \right)\), khi đó \(d\left( {I,\left( P \right)} \right) = \sqrt 6 \).
Trong không gian \(Oxyz\), cho điểm \(M\left( {2; - 1;3} \right)\) và mặt phẳng \(\left( P \right):3x - 2y + z + 1 = 0\). Phương trình mặt phẳng đi qua \(M\) và song song với \(\left( P \right)\) là
\(3x - 2y + z + 11 = 0\).
\(2x - y + 3z - 14 = 0\).
\(3x - 2y + z - 11 = 0\).
\(2x - y + 3z + 14 = 0\).
Cho các hàm số \(f\left( x \right),g\left( x \right)\) lần lượt có nguyên hàm \(F\left( x \right) = \left( {ax + 2} \right)\sqrt {x - b} ,G\left( x \right) = \frac{3}{{c{x^2}}}\) với \(a,b,c \in \mathbb{Z},c \ne 0\).
a)\(f\left( x \right) = \frac{a}{{2\sqrt {x - b} }}\).
b) \(\int {xG\left( x \right)} dx = 3\ln \left| {cx} \right| + C\).
c) Nếu \(c = - 6\) thì \(g'\left( x \right) = \frac{3}{{{x^4}}}\).
d) Nếu \(f\left( x \right) = \frac{{3x - 5}}{{\sqrt {x - 3} }}\) thì \(2{a^2} - 3b = - 1\).
Cho hàm số \(y = f\left( x \right) = - 3{x^2} + 6x\). Biết \(f\left( x \right)\) có một nguyên hàm \(F\left( x \right)\) thỏa mãn \(F\left( 0 \right) = 1\).
a)\(F\left( x \right) = - {x^3} + 3{x^2} + 1\).
b)\(\int\limits_0^1 {{f^2}\left( x \right)dx} = \left. {{F^2}\left( x \right)} \right|_0^1\).
c) Diện tích hình thang cong giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và các đường thẳng \(x = \frac{1}{2},x = \frac{3}{2}\) là \(F\left( {\frac{1}{2}} \right) - F\left( {\frac{3}{2}} \right)\).
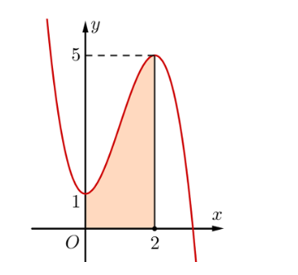
d) Phần tô đậm trong hình sau là hình thang cong giới hạn bởi đồ thị hàm số \(y = F\left( x \right)\), trục hoành và các đường thẳng \(x = 0,x = 2\).
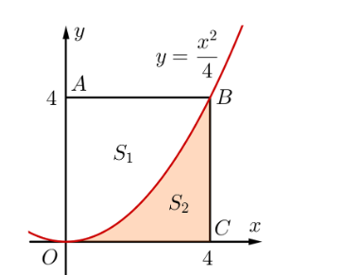
Hình vuông \(OABC\) có cạnh bằng 4 được chia thành hai phần bởi đường cong \(\left( C \right)\) có phương trình \(y = \frac{1}{4}{x^2}\). Gọi \({S_1},{S_2}\) lần lượt là diện tích của phần không tô đậm và tô đậm như hình vẽ sau.
a) \({S_2} = \left. {\frac{{{x^3}}}{{12}}} \right|_0^4\).
b) \({S_1} = \int\limits_0^4 {\left( {\frac{{{x^2}}}{4} - 4} \right)dx} \).
c)\(0 < {S_1} < 2{S_2}\).
d) Tỉ số \(\frac{{{S_1}}}{{{S_2}}}\) là một số nguyên.
Trong không gian với hệ trục tọa độ \(Oxyz\), mặt phẳng \(\left( \alpha \right)\)qua hai điểm \(A\left( {1;2;1} \right),B\left( { - 2;1;3} \right)\) và cách đều hai điểm \(C\left( {2; - 1;3} \right),D\left( {0;3;1} \right)\) có dạng \(3x + by + cz + d = 0\).
a) Điểm \(A\left( {1;2;1} \right)\) cách mặt phẳng \(\left( {Oxy} \right)\) một khoảng bằng 1.
b) \(I\left( {1;1;2} \right)\) là trung điểm đoạn thẳng \(CD\).
c) Nếu \(\left( \alpha \right)//CD\) thì \(2b - 3c + d = - 31\).
d) Nếu \(\left( \alpha \right)\) đi qua trung điểm \(I\left( {1;1;2} \right)\) của \(CD\) thì \(2b - 3c + d = - 16\).
Cho hàm số \(y = f\left( x \right)\) có \(\int {f\left( x \right)dx} = x\sin x + C\). Tính \(f\left( {\frac{\pi }{2}} \right)\).
Biết \(\int\limits_0^{\frac{\pi }{3}} {\frac{{1 - \cos 2x}}{{1 + \cos 2x}}dx} = a\sqrt 3 + \frac{\pi }{b}\)\(\left( {a,{\mkern 1mu} {\mkern 1mu} b \in \mathbb{Z}} \right)\). Tính \(a + b\).
Cho parabol \(\left( P \right):y = {x^2}\) và hai điểm \(A,B\) thuộc \(\left( P \right)\) sao cho \(AB = 2\). Biết \(A\left( {a;{a^2}} \right),B\left( {b;{b^2}} \right)\) sao cho diện tích hình phẳng giới hạn bởi \(\left( P \right)\) và đường thẳng \(AB\) đạt giá trị lớn nhất. Tìm \(a + b\).
Từ một khúc gỗ hình trụ có đường kính 30 cm, người ta cắt khúc gỗ bởi một mặt phẳng đi qua đường kính đáy và nghiêng với đáy một góc \(45^\circ \) để lấy một hình nêm (xem hình minh họa).
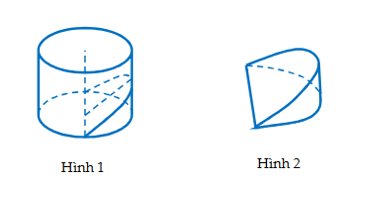
Tính thể tích của hình nêm (đơn vị cm3).
Trong không gian với hệ tọa độ \[Oxyz\], cho hai điểm \(A\left( {1;\,2;\,1} \right),B\left( {3;\,4;\,0} \right)\), mặt phẳng \(\left( P \right):ax + by + cz + 46 = 0\). Biết rằng khoảng cách từ \(A,\,B\) đến mặt phẳng \(\left( P \right)\) lần lượt bằng \(6\) và \(3\). Giá trị của biểu thức \(T = a + b + c\) bằng
\( - 3\).
\( - 6\).
\(3\).
\(6\).
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = AA' = 2a,AD = 4a.\)Với \(a = 3\), tính khoảng cách từ \(C\) đến mặt phẳng \(\left( {AB'D'} \right)\).








