Bộ 10 đề thi giữa kì 2 Toán 12 Chân trời sáng tạo cấu trúc mới có đáp án (Đề 2)
22 câu hỏi
Mệnh đề nào sau đây sai?
\(\int {\left( {f\left( x \right) - g\left( x \right)} \right){\rm{d}}x} = \int {f\left( x \right){\rm{d}}x} - \int {g\left( x \right){\rm{d}}x} \), với mọi hàm số \(f\left( x \right);g\left( x \right)\) liên tục trên \(\mathbb{R}.\)
\(\int {kf\left( x \right){\rm{d}}x} = k\int {f\left( x \right){\rm{d}}x} \), với mọi hằng số \(k\) và với mọi hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\).
\(\int {\left( {f\left( x \right) + g\left( x \right)} \right){\rm{d}}x} = \int {f\left( x \right){\rm{d}}x} + \int {g\left( x \right){\rm{d}}x} \), với mọi hàm số \(f\left( x \right);g\left( x \right)\) liên tục trên \(\mathbb{R}.\)
\(\int {f'\left( x \right){\rm{d}}x} = f\left( x \right) + C\) với mọi hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\).
Cho biết \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\). Tìm \(I = \int {\left[ {2f\left( x \right) + 1} \right]{\rm{d}}x} \).
\(I = 2F\left( x \right) + 1 + C\).
\(I = 2xF\left( x \right) + 1 + C\).
\(I = 2xF\left( x \right) + x + C\).
\(I = 2F\left( x \right) + x + C\).
Nếu \(\int\limits_1^2 {f(x){\rm{d}}x} = 5\) và \(\int\limits_2^3 {f(x){\rm{d}}x} = - 2\) thì \(\int\limits_1^3 {f(x){\rm{d}}x} \) bằng
\[3\].
\[7\].
\[ - 10\].
\[ - 7\].
Cho hàm số \(f(x)\) và \(F(x)\) liên tục trên \(\mathbb{R}\) thỏa \(F'(x) = f(x),\forall x \in \mathbb{R}\). Biết \(F(0) = 2\) và \(F(1) = 9\), mệnh đề nào sau đây đúng?
\(\int_0^1 f (x){\rm{d}}x = - 3\).
\(\int_0^1 f (x){\rm{d}}x = 7\).
\(\int_0^1 f (x){\rm{d}}x = 1\).
\(\int_0^1 f (x){\rm{d}}x = 3\).
Diện tích \[S\] của hình phẳng giới hạn bởi đường cong \[y = 3{x^2} + 1\], trục hoành và hai đường thẳng \[x = 0,x = 2\] được tính bởi công thức
\[S = \int\limits_0^2 {{{\left( {3{x^2} + 1} \right)}^2}dx} \].
\[S = \pi \int\limits_0^2 {{{\left( {3{x^2} + 1} \right)}^2}dx} \].
\[S = \int\limits_0^2 {\left( {3{x^2} + 1} \right)dx} \].
\[S = \pi \int\limits_0^2 {\left( {3{x^2} + 1} \right)dx} \].
Diện tích hình phẳng giới hạn bởi các đường \[y = {x^2}\] và \[y = 4x - 3\] là
\[S = \frac{3}{4}\].
\[S = \frac{4}{3}\].
\[S = \frac{2}{3}\].
\[S = 2\].
Trong không gian \(Oxyz\), mặt phẳng \(\left( P \right):x + y + z + 1 = 0\) có một vectơ pháp tuyến là
\(\overrightarrow {{n_1}} = \left( { - 1;1;1} \right)\).
\(\overrightarrow {{n_4}} = \left( {1;1; - 1} \right)\).
\(\overrightarrow {{n_3}} = \left( {1;1;1} \right)\).
\(\overrightarrow {{n_2}} = \left( {1; - 1;1} \right)\).
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha \right):x + y + 2z - 1 = 0\). Mặt phẳng \(\left( \alpha \right)\) song song với mặt phẳng nào sau đây?
\(\left( Q \right):3x + 3y + 6z - 1 = 0\).
\(\left( P \right):2x + 2y + 4z - 2 = 0\).
\(\left( R \right):x + y - z - 1 = 0\).
\(\left( S \right): - x - y - 2z + 1 = 0\).
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right)\,:\,x - 3y + 5z - 2 = 0\). Điểm nào dưới đây thuộc mặt phẳng \(\left( P \right)\)?
\(N\left( {1\,;\,1\,;\,7} \right)\).
\(Q\left( {4\,;\,4\,;\,2} \right)\).
\(P\left( {4\,;\, - 1\,;\,3} \right)\).
\(M\left( {0\,;\,0\,;\,2} \right)\).
Cho mặt phẳng\[\left( P \right):x + 2y + 2z - 6 = 0\]; \[M\left( {1\,;\,2\,;\,3} \right)\]. Khoảng cách từ \(M\) đến \(\left( P \right)\) bằng
\[d\left( {M,\,\left( P \right)} \right) = \frac{5}{9}\].
\[d\left( {M,\,\left( P \right)} \right) = \frac{{11}}{9}\].
\[d\left( {M,\,\left( P \right)} \right) = \frac{{11}}{3}\].
\[d\left( {M,\left( P \right)} \right) = \frac{5}{3}\].
Trong không gian \[Oxyz\], cho 3 điểm\(M\left( {2;1; - 3} \right)\), \(N\left( {1;0;2} \right)\); \(P\left( {2; - 3;5} \right)\). Tìm một vectơ pháp tuyến \(\overrightarrow n \) của mặt phẳng \(\left( {MNP} \right)\).
\(\overrightarrow n = \left( {12;4;8} \right)\).
\(\overrightarrow n = \left( {8;12;4} \right)\).
\(\overrightarrow n = \left( {3;1;2} \right)\).
\(\overrightarrow n = \left( {3;2;1} \right)\).
Trong không gian với hệ tọa độ \(Oxyz\), cho điểm \(A\left( {2;0; - 4} \right)\). Mặt phẳng trung trực của đoạn thẳng \(OA\) có phương trình là
\[x - 2y - 5z = 0\].
\[x - 2y - 5 = 0\].
\[x - 2z - 5 = 0\].
\[x - 2z - 10 = 0\].
Cho hàm số \(f\left( x \right) = - 6x + 7\).
a) Nếu \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) thì \(F'\left( 4 \right) = - 17\).
b)\(F\left( x \right) = - 3{x^2} + 7x + 21\) là một nguyên hàm của \(f\left( x \right)\).
c) Nếu \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) và \(F\left( 1 \right) = 2\) thì \(F\left( 2 \right) = - 4\).
d) Nếu \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) thì \(F\left( { - x} \right)\) là một nguyên hàm của \(f\left( { - x} \right)\).
Một chất điểm chuyển động trên đường thẳng nằm ngang (chiều dương hướng sang phải) với gia tốc phụ thuộc vào thời gian \(t\left( s \right)\) là \(a\left( t \right) = 2t - 7\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\). Biết vận tốc ban đầu bằng \(6{\rm{m/s}}\).
a) Vận tốc tức thời của chất điểm tại thời điểm \(t\left( s \right)\) xác định bởi \(v\left( t \right) = {t^2} - 7t + 10\).
b) Tại thời điểm \(t = 7\left( {\rm{s}} \right)\), vận tốc của chất điểm là \(6\left( {{\rm{m/s}}} \right)\).
c) Độ dịch chuyển của vật trong khoảng thời gian \(1 \le t \le 7\) là \(18{\rm{m}}\).
d) Trong 8 giây đầu tiên, thời điểm chất điểm xa nhất về phía bên phải là \(t = 7\left( {\rm{s}} \right)\).
Cho hàm số \(y = f\left( x \right)\) liên tục và có đồ thị như hình vẽ sau. Biết diện tích các miền \(A,B,C\) lần lượt là \({S_A} = 2,35,{S_B} = 4,3,{S_C} = 8,35\).
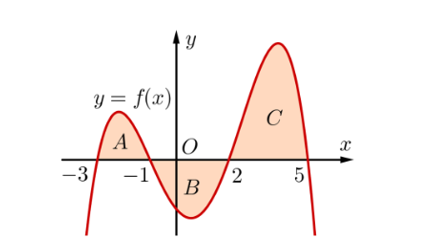
a) \(\int\limits_{ - 3}^2 {f\left( x \right)dx} = 6,65\).
b) \(\int\limits_{ - 1}^5 {\left| {f\left( x \right)} \right|dx = 12,65} \).
c) \(\int\limits_{ - 3}^5 {\left[ {f\left( x \right) + 1} \right]dx} = 7,4\).
d)\(\int\limits_{ - 1}^5 {\left[ {2x + f\left( x \right)} \right]dx} = 16,05\).
Trong không gian với hệ trục tọa độ \(Oxyz\) cho điểm \(A\left( {0; - 1;1} \right)\) và hai vectơ \(\overrightarrow u = \left( { - 1;0;2} \right)\) và \(\overrightarrow v = \left( {2;1;0} \right)\).
a) Mặt phẳng \(\left( P \right)\) đi qua \(A\) nhận \(\overrightarrow u \) làm vectơ pháp tuyến có phương trình là \( - x + 2z - 2 = 0.\)
b) Mặt phẳng \(\left( Q \right)\) đi qua \(A\) và nhận \(\overrightarrow u ,\overrightarrow v \) làm vặp vectơ chỉ phương có phương trình \(2x - 4y - z - 3 = 0\).
c) Mặt phẳng đi qua ba điểm \(A,B\left( { - 3;1;2} \right),C\left( {1;0;1} \right)\) có phương trình \(x - y + 5z - 6 = 0\).
d) Gọi \(M\) là giao điểm của \(\left( P \right)\) và trục \(Ox\), \(N\)là giao điểm của \(\left( Q \right)\) và trục \(Oz\). Mặt phẳng đi qua ba điểm \(A,M,N\) có phương trình là \(3x + 8y + 2z + 6 = 0\).
Biết \(F\left( x \right) = a{x^2} + bx + 1,\left( {a;b \in \mathbb{R}} \right)\) là nguyên hàm của hàm số \(f\left( x \right) = 2x + 1\). Tổng \(a + b\) bằng bao nhiêu?
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\). Gọi \(F\left( x \right),G\left( x \right)\) là hai nguyên hàm của \(f\left( x \right)\) trên \(\mathbb{R}\) thỏa mãn \(F\left( 2 \right) + G\left( 2 \right) = 8\) và \(F\left( 0 \right) + G\left( 0 \right) = - 2\). Khi đó \(\int\limits_0^{16} f \left( {\frac{x}{8}} \right){\rm{d}}x\) bằng bao nhiêu?
Một người lái xe ô tô đang chạy với vận tốc 20 m/s thì người lái xe phát hiện có hàng rào ngăn đường ở phía trước cách 45 m (tính từ vị trí đầu xe đến hàng rào) vì vậy, người lái xe đạp phanh. Từ thời điểm đó xe chuyển động chậm dần đều với vận tốc \(v\left( t \right) = - 5t + 20\left( {{\rm{m/s}}} \right)\), trong đó \(t\) là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, xe ô tô còn cách hàng rào ngăn cách bao nhiêu mét (tính từ vị trí đầu xe đến hàng rào)?
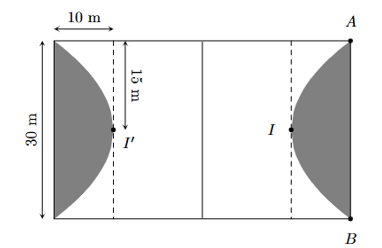
Ông An xây dựng một sân bóng đá mini hình chữ nhật có chiều rộng 30 m và chiều dài 50 m. Để giảm bởi chi phí cho việc trồng cỏ nhân tạo, ông An chia sân bóng ra làm hai phần (tô đen và không tô đen) như hình vẽ. Phần tô đen gồm hai phần diện tích bằng nhau và đường cong \(AIB\) là một parabol đỉnh I được trồng cỏ nhân tạo với giá 130000 đồng/m2 và phần còn lại được trồng với giá 90000 đồng/m2. Hỏi ông An phải trả bao nhiêu tiền (triệu đồng) để trồng cỏ nhân tạo cho sân bóng đá.
Trong không gian \(Oxyz,\) cho mặt phẳng \((\alpha ):x + by + cz + d = 0\) vuông góc với mặt phẳng \((\beta ):x + 2y + 3z + 4 = 0\) và chứa giao tuyến của hai mặt phẳng \((P):x + 3y + z - 7 = 0,\)\((Q):x - y + z + 1 = 0.\) Khi đó \(d\) bằng bao nhiêu?
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):x - z + 10 = 0\) và điểm \(A\left( {1;0;0} \right)\). Mặt phẳng \(\left( \alpha \right)\) đi qua \(A\), vuông góc với \(\left( P \right)\), cách gốc tọa độ \(O\) một khoảng bằng \(\frac{2}{3}\) và cắt các tia \(Oy,Oz\) lần lượt tại các điểm \(B,C\) không trùng \(O\). Thể tích khối tứ diện \(OABC\) bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?








