Bộ 10 đề thi giữa kì 2 Toán 12 Chân trời sáng tạo cấu trúc mới có đáp án (Đề 1)
22 câu hỏi
Họ tất cả các nguyên hàm của hàm số \(f\left( x \right) = 2x + 5\) là
\({x^2} + 5x + C.\)
\(2{x^2} + 5x + C.\)
\(2{x^2} + C.\)
\({x^2} + C.\)
Mệnh đề nào dưới đây đúng?
\({\left( {\int {f\left( x \right){\rm{d}}x} } \right)^\prime } = f'\left( x \right)\).
\({\left( {\int {f\left( x \right){\rm{d}}x} } \right)^\prime } = - f\left( x \right)\).
\({\left( {\int {f\left( x \right){\rm{d}}x} } \right)^\prime } = - f'\left( x \right)\).
\({\left( {\int {f\left( x \right){\rm{d}}x} } \right)^\prime } = f\left( x \right)\).
Biết \[\int\limits_0^1 {f\left( x \right)dx = - 2} \] và \[\int\limits_0^1 {g\left( x \right)dx = 3} ,\] khi đó \[\int\limits_0^1 {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} \] bằng
\[ - 5.\]
\[5.\]
\[ - 1.\]
\[1.\]
Cho \(f\left( x \right)\) là hàm số liên tục trên đoạn \(\left[ {1;2} \right]\). Biết \(F\left( x \right)\) là nguyên hàm của \(f\left( x \right)\) trên đoạn \(\left[ {1;2} \right]\) thỏa mãn \(F\left( 1 \right) = - 2\) và \(F\left( 2 \right) = 4\). Khi đó \(\int\limits_1^2 {f\left( x \right){\rm{d}}} x\) bằng
\(6\).
\(2\).
\( - 6\).
\( - 2\).
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\). Gọi \(S\) là diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right),y = 0,x = - 1\) và \(x = 4\) (như hình vẽ bên). Mệnh đề nào dưới đây là đúng?
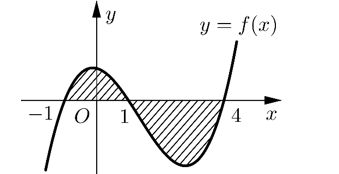
\(S = - \int\limits_{ - 1}^1 {f\left( x \right)dx} + \int\limits_1^4 {f\left( x \right)dx} \).
\(S = \int\limits_{ - 1}^1 {f\left( x \right)dx} - \int\limits_1^4 {f\left( x \right)dx} \).
\(S = \int\limits_{ - 1}^1 {f\left( x \right)dx} + \int\limits_1^4 {f\left( x \right)dx} \).
\(S = - \int\limits_{ - 1}^1 {f\left( x \right)dx} - \int\limits_1^4 {f\left( x \right)dx} \).
Họ tất cả các nguyên hàm của hàm số \(f\left( x \right) = \frac{{2x - 1}}{{{{\left( {x + 1} \right)}^2}}}\) trên khoảng \(\left( { - 1; + \infty } \right)\) là
\(2\ln \left( {x + 1} \right) + \frac{2}{{x + 1}} + C\).
\(2\ln \left( {x + 1} \right) + \frac{3}{{x + 1}} + C\).
\(2\ln \left( {x + 1} \right) - \frac{2}{{x + 1}} + C\).
\(2\ln \left( {x + 1} \right) - \frac{3}{{x + 1}} + C\).
Trong không gian \(Oxyz\), phương trình của mặt phẳng \[\left( {Oxy} \right)\] là
\(y = 0\).
\(x = 0\).
\(z = 0\).
\(x + y = 0\).
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha \right):3x + 2y - 4z + 1 = 0\). Vectơ nào dưới đây là một vectơ pháp tuyến của \(\left( \alpha \right)\)?
\(\overrightarrow {{n_2}} = \left( {3\,;\,2\,;\,4} \right)\).
\(\overrightarrow {{n_3}} = \left( {2\,;\, - 4\,;\,1} \right)\).
\(\overrightarrow {{n_1}} = \left( {3\,;\, - 4\,;\,1} \right)\).
\(\overrightarrow {{n_4}} = \left( {3\,;\,2\,;\, - 4} \right)\).
Trong không gian \(Oxyz\), mặt phẳng đi qua \(O\) và nhận vectơ \(\overrightarrow n = \left( {1;\, - 2;\,5} \right)\) làm vectơ pháp tuyến có phương trình là
\(x + 2y - 5z = 0\).
\(x + 2y - 5z + 1 = 0\).
\(x - 2y + 5z = 0\).
\(x - 2y + 5z + 1 = 0\).
Mặt phẳng \[(P)\] song song với giá của hai vectơ \(\overrightarrow {{u_1}} = \left( { - 1; - 3; - 3} \right),\;\,\overrightarrow {{u_2}} = \left( {3; - 1;1} \right)\) có một vectơ pháp tuyến là
\(\overrightarrow n = \left( { - 6;8;10} \right)\).
\(\overrightarrow n = \left( { - 6; - 8;10} \right)\).
\(\overrightarrow n = \left( {6; - 8;10} \right)\).
\(\overrightarrow n = \left( {6;8;10} \right)\).
Trong không gian \(Oxyz\), cho ba điểm \(A\left( {2; - 1;3} \right)\), \(B\left( {4;0;1} \right)\), \(C\left( { - 10;5;3} \right)\). Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng \(\left( {ABC} \right)\)?
A. \(\left( {1;2;2} \right)\). B. \(\left( {1; - 2;2} \right)\). C. \(\left( {1;2;0} \right)\). D. \(\left( {1;8;2} \right)\).
Trong không gian \[Oxyz\], cho hai điểm \(M\left( {2;1;3} \right)\) và \(N\left( {4;3; - 5} \right)\). Mặt phẳng trung trực của đoạn thẳng \(MN\) có vectơ pháp tuyến là
\[\overrightarrow {{n_1}} = \left( {2;1;3} \right)\].
\[\overrightarrow {{n_2}} = \left( {4;3; - 5} \right)\].
\[\overrightarrow {{n_3}} = \left( {1;1; - 4} \right)\].
\[\overrightarrow {{n_4}} = \left( {1;1;4} \right)\].
Cho hàm số \(f\left( x \right)\)có đạo hàm liên tục trên khoảng \(\left( {0; + \infty } \right)\) thỏa mãn \(f'\left( x \right) = \frac{{2{x^4} + 3}}{{{x^2}}}\) và \(f\left( 1 \right) = 2\).
a)\(f\left( x \right) = \frac{{2{x^3}}}{3} - \frac{3}{x} + C\).
b)\(f\left( x \right) = \frac{{2{x^3}}}{3} - \frac{3}{x} - \frac{{13}}{3}\).
c) \(f\left( 2 \right) = \frac{{49}}{6}\).
d) Diện tích hình thang cong giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và các đường thẳng \(x = 1,x = 2\) là \(S = f\left( 2 \right) - f\left( 1 \right)\).
Sau khi xuất phát, ô tô di chuyển với tốc độ \(v\left( t \right) = 2,01t - 0,025{t^2}\left( {0 \le t \le 10} \right)\). Trong đó \(v\left( t \right)\)tính theo m/s, thời gian \(t\) tính theo giây với \(t = 0\) là thời điểm xe xuất phát.
a) Quãng đường xe di chuyển được tính theo công thức là \(s\left( t \right) = 2,01 - 0,05t\left( {0 \le t \le 10} \right)\).
b) Quãng đường xe di chuyển được trong 3 giây là 8,82 m.
c) Quãng đường xe di chuyển được trong giây thứ 9 xấp xỉ \(15,277\)m.
d) Trong khoảng thời gian không quá 10 giây đầu, khi vận tốc đạt giá trị lớn nhất thì gia tốc của xe là \(1,51\;{\rm{m/}}{{\rm{s}}^{\rm{2}}}\).
Cho hình phẳng \(\left( H \right)\) có diện tích \(S\), giới hạn bởi các đường \(y = {x^2} - 2x,y = 0,x = - 10,x = 10\).
a) \(S = \int\limits_{ - 10}^{10} {\left| {{x^2} - 2x} \right|dx} \).
b)\(S = \int\limits_{ - 10}^0 {\left( {{x^2} - 2x} \right)dx} + \int\limits_0^2 {\left( {{x^2} - 2x} \right)dx} + \int\limits_2^{10} {\left( {{x^2} - 2x} \right)dx} \).
c) Diện tích hình phẳng \(\left( H \right)\) là \(\frac{{2000}}{3}\).
d) Khi quay \(\left( H \right)\) quanh trục \(Ox\) ta được khối tròn xoay có thể tích là \(\frac{{128000}}{3}\).
Trong không gian với hệ trục tọa độ \(Oxyz\), cho các điểm \(A\left( {0;1;2} \right),B\left( {2; - 2;2} \right),C\left( { - 2;0;1} \right)\) và các mặt phẳng \(\left( \alpha \right):3x - 2y + 2z + 7 = 0\) và \(\left( \beta \right):5x - 4y + 3z + 1 = 0\).
a)\(\overrightarrow {AB} = \left( {2; - 3; - 2} \right)\).
b) Mặt phẳng \(\left( \alpha \right):3x - 2y + 2z + 7 = 0\) không đi qua gốc tọa độ.
c) Phương trình mặt phẳng đi qua ba điểm \(A,B,C\) là \(x + 6y - 8z + 1 = 0\).
d) Phương trình mặt phẳng đi qua điểm \(A\left( {0;1;2} \right)\) và vuông góc với hai mặt phẳng \(\left( \alpha \right),\left( \beta \right)\) thì mặt phẳng đi qua điểm \(T\left( {3;3;6} \right)\).
Cho hàm số \[f(x)\]có \[f\left( {\frac{\pi }{2}} \right) = 4\]và\(f'\left( x \right) = \frac{2}{{{{\sin }^2}x}} + 1,\forall x \in \left( {0;\pi } \right)\).
Biết \(f\left( x \right) = - a\cot x + x + b + \frac{\pi }{c}\). Tính \(a + b + c.\)
Hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có \(f\left( 0 \right) = 2\) và \(f\left( {4x} \right) - f\left( x \right) = 4{x^3} + 2x,\,\forall x \in \mathbb{R}.\) Tính \(I = \int\limits_0^1 {f\left( x \right)dx} \) (kết quả làm tròn đến hàng phần trăm).
Một ô tô đang chạy đều với vận tốc \(a\left( {{\rm{m/s}}} \right)\) thì người lái đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc \(v\left( t \right) = - 5t + a\left( {{\rm{m/s}}} \right)\), trong đó \(t\) là thời gian tính bằng giây kể từ lúc đạp phanh. Hỏi vận tốc ban đầu \(a\) của ô tô là bao nhiêu (m/s), biết từ lúc đạp phanh đến khi dừng hẳn ô tô di chuyển được 40 mét.
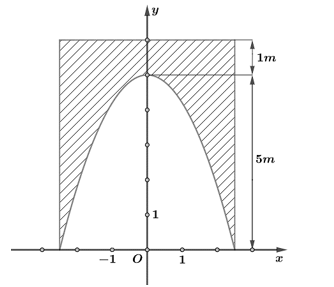
Ông \(A\) có một cái cổng hình chữ nhật, lối vào cổng có dạng parabol có kích thước như hình vẽ. Ông \(A\) cần trang trí bề mặt (phần gạch chéo) của cổng. Ông \(A\) cần bao nhiêu tiền để trang trí, biết giá thành trang trí là \(1200000\)đồng\(/{\rm{1}}{{\rm{m}}^{\rm{2}}}\) (đơn vị triệu đồng)?
Trong không gian \(Oxyz\), cho \(A\left( {2;0;0} \right),B\left( {0;4;0} \right),C\left( {0;0;6} \right),D\left( {2;4;6} \right)\). Gọi \(\left( P \right)\) là mặt phẳng song song song với mặt phẳng \(\left( {ABC} \right)\), \(\left( P \right)\) cách đều \(D\) và mặt phẳng \(\left( {ABC} \right)\) có dạng \(6x + by + cz + d = 0\). Tính \(b + c + d\).
Trong không gian \(Oxyz\), cho bốn điểm \(A\left( {a;0;0} \right),B\left( {0;b;0} \right),C\left( {0;0;c} \right),D\left( {1;2; - 1} \right)\),với \(a,b,c\)là các số thực khác \(0\). Biết rằng bốn điểm\(A,B,C,D\)đồng phẳng, khi khoảng cách từ gốc toạ độ \(O\) đến mặt phẳng \(\left( {ABC} \right)\)lớn nhất. Giá trị \(a + b + c\)bằng bao nhiêu?








