12 câu hỏi
Số đối của số hữu tỉ \( - 0,2\) là
\(0,2.\)
\( - \frac{1}{5}.\)
\(5.\)
\( - 5.\)
Cho hai số hữu tỉ \(a\) và \(b\) được biểu diễn trên trục số như sau.

Chọn khẳng định đúng.
\(b > 0 > a.\)
\(b > a > 0.\)
\(b < a < 0.\)
\(b < 0 < a.\)
Giá trị của \({\left( {\frac{3}{5}} \right)^3}\) bằng
\(\frac{9}{{15}}.\)
\(\frac{{27}}{{125}}.\)
\(\frac{{ - 9}}{{15}}.\)
\(\frac{{ - 27}}{{125}}.\)
Cho các số hữu tỉ \(a,\,\,b,\,\,c,\,\,d\) thỏa mãn \(a - b + c = d.\) Khi đó
\(a - b + c + d = 0.\)
\(a = b + c + d.\)
\(b = d - a - c.\)
\(c = b - a + d.\)
Trong các số sau, số nào là số thập phân vô hạn tuần hoàn?
\(2,3.\)
\(3,7557.\)
\( - 0,25.\)
\( - 6,12\left( {63} \right).\)
Số \(\sqrt 5 \) là
Số tự nhiên.
Số nguyên.
Số hữu tỉ.
Số vô tỉ.
Căn bậc nào sau đây là sai?
\(\sqrt {{{\left( { - 5} \right)}^2}} = - 5.\)
\(\sqrt {25} = 5.\)
\( - \sqrt 9 = - 3.\)
\(\sqrt {{x^2}} = \left| x \right|.\)
Trong các phát biểu sau, phát biểu nào là sai?
Nếu \(a \in \mathbb{Z}\) thì \(a \in \mathbb{R}.\)
Nếu \(a \in \)𝕀 thì \(a \notin \mathbb{R}.\)
Nếu \(a \in \mathbb{N}\) thì \(a \in \mathbb{Z}.\)
Nếu \(a \notin \mathbb{Q}\) thì \(a \in \)𝕀.
Khẳng định nào sau đây là đúng?
Hai góc đối đỉnh thì bù nhau.
Hai góc đối đỉnh thì bằng nhau.
Hai góc bằng nhau thì đối đỉnh.
Hai góc đối đỉnh thì phụ nhau.
Cho tia \(Ot\) là tia phân giác của góc \(xOy\). Khẳng định nào sau đây là đúng nhất?
\(\widehat {xOy} = \widehat {yOt.}\)
\(\widehat {xOt} + \widehat {yOt} = \widehat {xOy}\).
\(\widehat {xOt} = \widehat {yOt} = \frac{{\widehat {xOy}}}{2}.\)
\(\widehat {xOy} - \widehat {yOt} = \widehat {xOt}.\)
Cho hình vẽ dưới đây. Hãy chọn đáp án đúng:
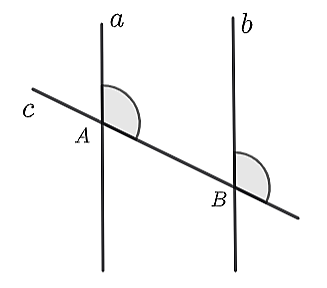
\(a\parallel b\) vì hai góc được kí hiệu trên hình vẽ là hai góc đồng vị bằng nhau.
\(a\parallel b\) vì hai góc được kí hiệu trên hình vẽ là hai góc so le trong bằng nhau.
\(a\parallel c\) vì hai góc được kí hiệu trên hình vẽ là hai góc so le trong bằng nhau.
\(c\parallel b\) vì hai góc được kí hiệu trên hình vẽ là hai góc so le trong bằng nhau.
Cho ba đường thẳng \(a,b,c\). Biết \(a\parallel b\), \(a\parallel c\) ta suy ra
\(c\parallel b.\)
\(b\) và \(c\) cắt nhau.
\(b\) vuông góc với \(c.\)
\(b\) vuông góc với \(a\) và \(c.\)
