12 câu hỏi
Khẳng định nào sau đây là đúng?
\(\frac{5}{9} \in \mathbb{Q}.\)
\(\frac{1}{3} \in \mathbb{Z}.\)
\(\frac{{ - 8}}{5} \notin \mathbb{Q}.\)
\( - 11 \in \mathbb{N}.\)
Cho hai số hữu tỉ \(a\) và \(b\) được biểu diễn trên trục số như sau.
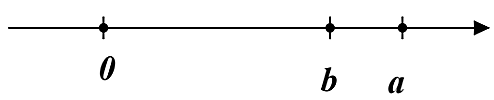
Khẳng định nào sau đây là đúng?
\(b > 0 > a.\)
\(b > a.\)
\(b < a < 0.\)
\(0 < b < a.\)
Biểu thức \({\left( { - \frac{2}{5}} \right)^3}\) bằng
\(\frac{4}{{25}}.\)
\(\frac{{ - 4}}{{25}}.\)
\(\frac{8}{{125}}.\)
\(\frac{{ - 8}}{{125}}.\)
Kết quả của phép tính \[{6^6}:{\left( { - 6} \right)^3}\] là
\[{\left( { - 6} \right)^3}\].
\[{6^3}\].
\[{6^2}\].
\[{\left( { - 6} \right)^2}\].
Phân số \(\frac{{11}}{{24}}\) được viết dưới dạng số thập phân vô hạn tuần hoàn là
\(0,\left( {458} \right)3.\)
\(0,45\left( {83} \right).\)
\(0,458\left( 3 \right).\)
\(0,458.\)
Khẳng định nào sau đây là đúng?
Số nguyên không là số thực.
\(\sqrt 2 ;{\rm{ }}\sqrt 3 ;{\rm{ }}\sqrt 5 \) là các số thực.
Số \(0\) vừa là số hữu tỉ vừa là số vô tỉ.
\(\frac{5}{3};{\rm{ }}\frac{1}{3};{\rm{ }}\frac{2}{3}\) là các số vô tỉ.
Số 9 là căn bậc hai số học của số
\(81.\)
\( - 81.\)
\(3.\)
\( - 3.\)
Số đối của số \(\sqrt 3 \) là:
\(\sqrt 3 \).
\( - \sqrt 3 \).
\(\frac{1}{{\sqrt 3 }}\).
\( - \frac{1}{{\sqrt 3 }}\).
Hai đường thẳng \(zz'\) và \(tt'\) cắt nhau tại \(A\).
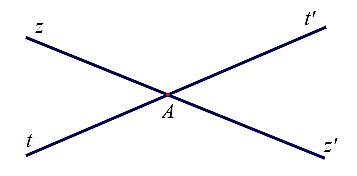
Góc đối đỉnh của \(\widehat {zAt'}\) là
\(\widehat {z'At'}.\)
\(\widehat {z'At}.\)
\(\widehat {zAt'}.\)
\(\widehat {zAt}.\)
Cho hình vẽ sau, khẳng định nào sau đây là sai?
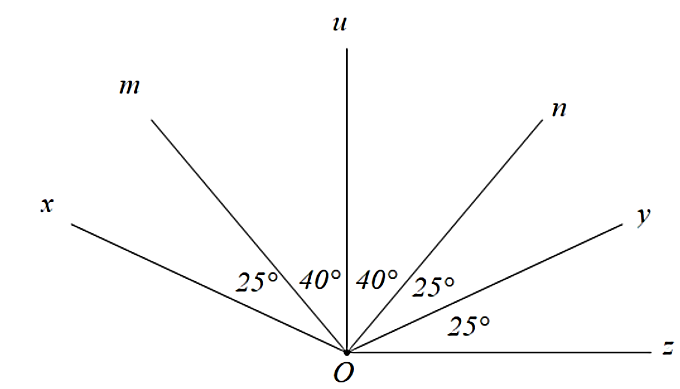
\(Ou\) là tia phân giác của \(\widehat {mOn}.\)
\(Ou\) là tia phân giác của \(\widehat {xOy}\).
\(Oy\) là phân giác của \(\widehat {nOz}\).
\(On\) là tia phân giác của \(\widehat {mOz}\).
Cho hình vẽ sau:
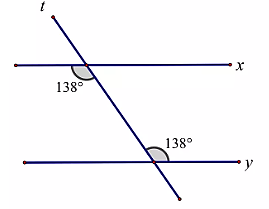
Khẳng định nào sau đây là đúng?
\(x\parallel y\) vì hai góc kí hiệu trên hình vẽ là hai góc đồng vị bằng nhau.
\(x\parallel y\) vì hai góc kí hiệu trên hình vẽ là hai góc so le trong bằng nhau.
\(x\parallel t\) vì hai góc kí hiệu trên hình vẽ là hai góc so le trong bằng nhau.
\(t\parallel y\) vì hai góc kí hiệu trên hình vẽ là hai góc so le trong bằng nhau.
Qua một điểm ở ngoài đường thẳng, ta kẻ được bao nhiêu đường thẳng song song với đường thẳng đó?
\(0.\)
\(1.\)
\(2.\)
Vô số.
