12 câu hỏi
A. TRẮC NGHIỆM (7,0 điểm)
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Cách viết nào sau đây biểu diễn một số hữu tỉ?
\(\frac{{6,5}}{{14}}.\)
\(\frac{3}{7}.\)
\(\frac{{21}}{0}.\)
\(\frac{{15}}{{0,2}}.\)
Trong các khẳng định sau, khẳng đính nào sai?
\({x^1} = x.\)
\({x^0} = 1{\rm{ }}\left( {x \ne 0} \right)\).
\({x^1} = 1.\)
\({x^{a + 1}} = {x^a}.x\).
Chọn phát biểu đúng. Với \(a,b,c \ne 0\)
Nếu \(a + b = c\) thì \(a = c - b.\)
Nếu \(a + b = c\) thì \(a = c + b.\)
Nếu \(a + b = c\) thì \(a = b - c.\)
Nếu \(a + b = c\) thì \(a = - c - b.\)
Số thập phân \(0,36363636.....\) được viết dưới dạng thu gọn (có chu kì trong dấu ngoặc) là
\(0,\left( {363} \right).\)
\(0,\left( {36} \right).\)
\(0,\left( 3 \right).\)
\(0,3\left( {63} \right)\).
Trong các số sau, đâu là số vô tỉ?
\(\sqrt {121} .\)
\(0,\left( {12} \right).\)
\(0,010010001...\)
\( - 3,12\left( {345} \right).\)
Căn bậc hai số học của \(81\) là
\(9\) và \( - 9\).
\(\frac{1}{{81}}.\)
\(9.\)
\(\frac{{81}}{2}.\)
Tập hợp các số thực có kí hiệu là
\(\mathbb{R}.\)
\(\mathbb{Q}.\)
\(\mathbb{Z}.\)
\(\mathbb{N}.\)
Trong các mệnh đề sau, mệnh đề nào đúng?
Nếu \(x \in \mathbb{Z}\) thì \(x \in \mathbb{R}\).
Nếu \(x \in \mathbb{R}\) thì \(x \in \mathbb{Q}\).
Nếu \(x \in \mathbb{Q}\) thì \(x \in \mathbb{Z}\).
Nếu \(x \in \mathbb{Z}\) thì \(x \in \mathbb{N}.\)
Quan sát hình vẽ. Góc kề bù với \(\widehat {xEn}\) là
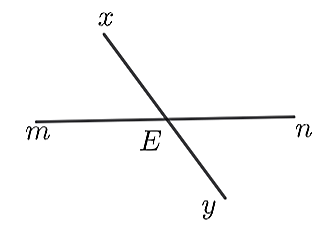
\(\widehat {mEy}.\)
\(\widehat {mEx}.\)
\(\widehat {nEy}.\)
\(\widehat {mEx}\) và \(\widehat {nEy}.\)
Chọn phát biểu đúng trong các phát biểu dưới đây:
\(\widehat {{H_1}}\) và \(\widehat {{K_1}}\) là hai góc so le trong.
\(\widehat {{H_4}}\) và \(\widehat {{K_4}}\) là hai góc đồng vị.
\(\widehat {{H_3}}\) và \(\widehat {{K_4}}\) là hai góc so le trong.
\(\widehat {{H_4}}\) và \(\widehat {{K_2}}\) là hai góc so le trong.
Cho đường thẳng \(c\) cắt hai đường thẳng \(a\) và \(b\) phân biệt và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì
\(a\) song song với \(b.\)
\(a\) cắt \(b.\)
\(a\) vuông góc với \(b\).
\(a\) trùng với \(b\).
Phát biểu đúng về tiên đề Euclid là
Qua một điểm ở ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.
Qua một điểm ở ngoài một đường thẳng, có vô số đường thẳng song song với đường thẳng đó.
Qua một điểm ở ngoài một đường thẳng, không kẻ được đường thẳng song song với đường thẳng đó.
Qua một điểm ở ngoài một đường thẳng, kẻ được ít nhất một đường thẳng song song với đường thẳng đó.
