Bộ 10 đề thi cuối kì 2 Toán 9 Chân trời sáng tạo có đáp án (Đề số 5)
20 câu hỏi
A. Trắc nghiệm
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn
Đồ thị của hàm số \[{x^2} + 2\left( {m + 3} \right)x + {m^2} + 6m = 0\,\] có trục đối xứng là
trục \[Ox\].
đường thẳng \[y = - x\].
đường thẳng \[y = x\].
trục \[Oy\].
Trong mặt phẳng tọa độ \[Oxy\], cho hàm số \(y = \left( {m + 2} \right){x^2}\) có đồ thị đi qua điểm \(\left( { - 1\,;\,\,3} \right).\) Khi đó giá trị của \[m\] tương ứng là
\(m = - 1.\)
\(m = 1.\)
\(m = 0.\)
\(m = 2.\)
Phương trình bậc hai \({x^2} - 3x + 7 = 0\) có biệt thức \(\Delta \) bằng
\(2\).
\( - 19\).
\( - 37\).
\(16\).
Gọi \({x_1},\,x{}_2\) là hai nghiệm của phương trình \({x^2} - 3x + 2 = 0\) khi đó ta có
\[{x_1} + {x_2} = 3;\,\,\,{x_1}{x_2} = 2.\]
\({x_1} + {x_2} = - 3;\,\,{x_1}{x_2} = 2.\)
\({x_1} + {x_2} = 3;\,\,{x_1}{x_2} = - 2.\)
\[{x_1} + {x_2} = - 3;\,\,{x_1}{x_2} = - 2.\]
Cỡ mẫu là
số giá trị của mẫu dữ liệu.
dãy dữ liệu.
số lần xuất hiện một giá trị trong mẫu dữ liệu.
số lần xuất hiện một số giá trị trong mẫu dữ liệu.
Bảng thống kê sau cho biết số lượt mượn các loại sách trong một tuần tại thư viện của một trường Trung học cơ sở như sau:
Loại sách | Sách giáo khoa | Sách tham khảo | Truyện ngắn | Tiểu thuyết |
Số lượt | 20 | 80 | 70 | 30 |
Từ bảng thống kê, tần số tương đối về số lượng sách giáo khoa được mượn là
\(10{\rm{\% }}\)
\(15{\rm{\% }}\).
\(35{\rm{\% }}\).
\[40{\rm{\% }}.\].
Thời gian hoàn thành một sản phẩm (tính bằng phút) của một số công nhân trong một tổ được biểu diễn ở biểu đồ dưới đây:
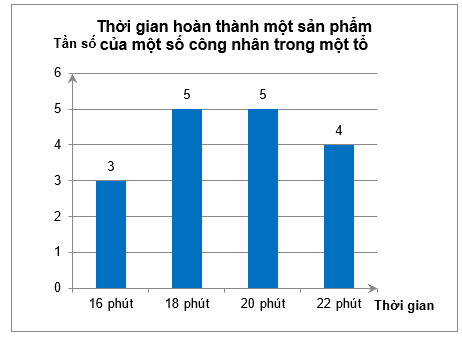
Thời gian hoàn thành một sản phẩm của công nhân chủ yếu là
5 phút.
17 phút.
18 phút và 20 phút.
20 phút và 22 phút.
Gieo một con xúc xắc cân đối và đồng chất. Không gian mẫu của phép thử có số phần tử là
3.
4.
5.
6.
Cho các hình vẽ:
Hình 1 |
Hình 2 |
Hình 3 |
Hình 4 |
Hình nào sau đây biểu diễn góc nội tiếp?
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Tứ giác nội tiếp đường tròn là
tứ giác có bốn đỉnh nằm trên đường tròn đó.
tứ giác có nhiều nhất bốn đỉnh nằm trên đường tròn đó.
tứ giác có tổng số đo hai góc đối nhau bằng \[90^\circ .\]
tứ giác có ba đỉnh nằm trên đường tròn đó.
Với một phép quay góc \(\alpha \) thì \(\alpha \) có thể nhận các giá trị:
\(0^\circ \le \alpha \le 180^\circ \).
\(0^\circ < \alpha < 180^\circ \).
\(0^\circ \le \alpha \le 360^\circ \).
\(0^\circ < \alpha < 360^\circ \).
Một lục giác đều và một ngũ giác đều chung cạnh \[AD\] (như hình vẽ). Số đo góc \(BAC\) là
\(30^\circ \).
\(36^\circ \).
\(60^\circ \).
\(66^\circ \).
Phần 2. Câu trắc nghiệm đúng sai
Cho phương trình \(2{x^2} + \left( {2m - 1} \right)x + m - 1 = 0\) với \(m\) là tham số, \(m \ne \frac{3}{2}.\)
a) Phương trình đã cho là phương trình bậc hai một ẩn.
b) Phương trình luôn có hai nghiệm \({x_1},\,{x_2}\) với mọi \(m \ne \frac{3}{2}.\)
c) Tổng và tích hai nghiệm của phương trình lần lượt là \({x_1} + {x_2} = \frac{{2m - 1}}{2};\,\,{x_1}{x_2} = \frac{{m - 1}}{2}.\)
d) Có một giá trị của \(m\) để phương trình có hai nghiệm \({x_1},\,{x_2}\) thoả mãn \[4x_1^2 + 2{x_1}{x_2} + 4x_2^2 = 1.\]
Cho hình bên là một thúng gạo vun đầy. Thúng có dạng nửa hình cầu với đường kính \[50\,\,{\rm{cm,}}\] phần gạo vun lên có dạng hình nón cao \[15\,\,{\rm{cm}}{\rm{.}}\]

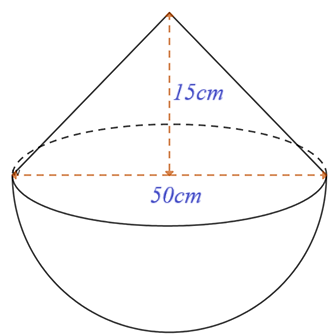
Nhà Danh dùng lon sữa bò cũ có dạng hình trụ (bán kính đáy bằng \[5\,\,{\rm{cm}},\] chiều cao \[15\,\,{\rm{cm}})\] để đong gạo mỗi ngày. Biết mỗi ngày nhà Danh ăn 5 lon gạo và mỗi lần đong thì lượng gạo chiếm \[90\% \] thể tích lon.
a) Thể tích hình cầu có bán kính đáy \(R\), được tính bằng công thức: \(V = \frac{4}{3}\pi {R^3}.\)
b) Phần gạo nằm ngang mặt thúng trở xuống có dạng nửa hình cầu có bán kính \[50\,\,{\rm{cm}}\].
c) Thể tích phần gạo trong thúng là \(\frac{{60\,\,625}}{3}\pi \,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right).\)
d) Với lượng gạo ở thúng trên thì nhà Danh có thể ăn nhiều nhất là 15 ngày.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn
Hai đội công nhân đắp đê ngăn triều cường. Nếu hai đội cùng làm thì trong 6 ngày xong việc. Nếu làm riêng thì đội I hoàn thành công việc nhanh hơn đội II là 9 ngày. Hỏi nếu làm riêng thì đội I đắp xong đê trong bao nhiêu ngày?
Tập hợp A có 24 số chia hết cho 5 và một số số không chia hết cho 5. Bạn An chọn ngẫu nhiên một số từ tập hợp A. Biết rằng xác suất của biến cố “Chọn được số không chia hết cho 5” là \[0,7.\] Hỏi tập hợp A có bao nhiêu phần tử?
Một trang trại nuôi gia súc có dạng hình tam giác đều cạnh 150 m (như hình vẽ). Người ta muốn đặt một trụ đèn cao áp tại một điểm cách đều ba đỉnh của tam giác đều. Tính khoảng cách từ điểm đó đến ba đỉnh của tam giác (làm tròn kết quả đến hàng phần mười).

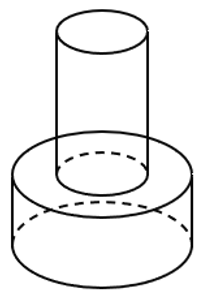
Một khối đồ chơi gồm hai khối trụ \(\left( {{H_1}} \right)\), \(\left( {{H_2}} \right)\) xếp chồng lên nhau, lần lượt có bán kính đáy và chiều cao tương ứng là \({r_1}\), \({h_1}\), \({r_2}\), \({h_2}\) thỏa mãn \({r_2} = \frac{1}{2}{r_1}\), \({h_2} = 2{h_1}\) (tham khảo hình vẽ). Biết rằng thể tích của toàn bộ khối đồ chơi bằng \(30{\rm{ c}}{{\rm{m}}^3}.\) Tính thể tích khối trụ \(\left( {{H_1}} \right)\).
B. Tự luận
1. Bạn Hoa được cô yêu cầu ghi lại thời gian chạy 1000 m của các bạn trong lớp (đơn vị: giây):
\[4:08\] | \[4:00\] | \[4:16\] | \[4:12\] | \[5:11\] | \[4:52\] | \[4:12\] | \[4:30\] | \[4:37\] |
\[5:12\] | \[5:00\] | \[5:17\] | \[5:14\] | \[4:13\] | \[4:22\] | \[4:02\] | \[4:05\] | \[5:42\] |
\[4:39\] | \[5:32\] | \[5:11\] | \[4:40\] | \[4:05\] | \[5:02\] | \[4:27\] | \[4:50\] | \[4:23\] |
\[5:48\] | \[5:22\] | \[4:37\] | \[4:23\] | \[5:00\] | \[5:18\] | \[5:17\] | \[4:49\] | \[5:12\] |
a) Để thu gọn bảng dữ liệu trên thì nên chọn bảng tần số không ghép nhóm hay tần số ghép nhóm để biểu thị dữ liệu? Tại sao?
b) Hãy chia số liệu làm 4 nhóm trong đó nhóm đầu tiên là \[4:00\] đến dưới \[4:30\]; lập bảng tần số và tần số tương đối ghép nhóm (làm tròn đến hàng đơn vị).
2. Viết ngẫu nhiên một số tự nhiên có hai chữ số nhỏ hơn 100.
Tính xác suất của mỗi biến cố \[A:\] “Số tự nhiên được viết ra là số tròn chục”.
Cho đường tròn \(\left( {O\,;\,\,R} \right)\) và đường thẳng \(d\) không đi qua \(O\) cắt đường tròn tại hai điểm \(A,\,\,B\). Lấy một điểm \(M\) trên tia đối của tia \(BA\) kẻ hai tiếp tuyến \(MC,\,\,MD\) với đường tròn \(\left( {C,\,\,\,D} \right.\) là hai tiếp điểm). Gọi \(H\) là trung điểm của \(AB.\)
a) Chứng minh rằng \(M,\,\,D,\,\,O,\,\,H\) cùng nằm trên một đường tròn.
b) Đoạn \(OM\) cắt đường tròn tại \(I.\) Chứng minh rằng \(I\) là tâm đường tròn nội tiếp tam giác \(MCD.\)
c) Đường thẳng qua \(O,\) vuông góc với \(OM\) cắt các tia \(MC,\,\,MD\) theo thứ tự tại \(P,\,\,Q.\) Tìm vị trí của điểm \(M\) trên \(d\) sao cho diện tích tam giác \(MPQ\) nhỏ nhất.












