Bộ 10 đề thi giữa kì 2 Toán 9 Chân trời sáng tạo có đáp án - Đề 07
5 câu hỏi
1. Xét các phương trình sau:
\[\sqrt 3 {x^2} - \left( {1 - \sqrt 3 } \right)x - 1 = 0;\] \[{x^2} - 6x - 8 = 0;\] \[ - 2{x^2} - 5x - 3 = 0;\] \[ - 2{x^2} - 5x + 7 = 0.\]
a) Trong các phương trình trên, phương trình nào có nghiệm \[x = - 1.\]
b) Với các phương trình nhận \[x = - 1\] là nghiệm, hãy tìm nghiệm còn lại của phương trình đó.
2. Giải bài toán sau bằng cách lập phương trình:
Một mảnh vườn hình chữ nhật \(ABCD\) có chu vi và diện tích lần lượt là \(70{\rm{\;m}}\) và \(250{\rm{\;}}{{\rm{m}}^2}.\) Người ta chia mảnh vườn đó thành ba khu vực: khu tiểu cảnh \(ADE,\) khu trồng hoa \(BEDF,\) khu thư giãn \(BCF\) với \(BE = DF = 6{\rm{\;m}}\) như mô tả ở hình bên.
![1. Xét các phương trình sau: \[\sqrt 3 {x^2} - \left( {1 - \sqrt 3 } \right)x - 1 = 0;\] \[{x^2} - 6x - 8 = 0;\] \[ - 2{x^2} - 5x - 3 = 0;\] \[ - 2{x^2} - 5x + 7 = 0.\] a) Trong các phương trình trên, phương trình nào có nghiệm \[x = - 1.\] b) Với các phương trình nhận \[x = - 1\] là nghiệm, hãy tìm nghiệm còn lại của phương trình đó. 2. Giải bài toán sau bằng cách lập phương trình: Một mảnh vườn hình chữ nhật \(ABCD\) có chu vi và diện tích lần lượt là \(70{\rm{\;m}}\) và \(250{\rm{\;}}{{\rm{m}}^2}.\) Người ta chia mảnh vườn đó thành ba khu vực: khu tiểu cảnh \(ADE,\) khu trồng hoa \(BEDF,\) khu thư giãn \(BCF\) với \(BE = DF = 6{\rm{\;m}}\) như mô tả ở hình bên. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/07/blobid5-1751341472.png)
Cho hàm số \(y = \left( {{m^2} - 1} \right){x^2}\) với \(m\) là tham số.
a) Tìm \(m\) để đồ thị hàm số đi qua điểm \(A\left( { - 1;2} \right)\).
b) Điểm \(B\left( {1;3} \right);C\left( { - 1;2} \right)\) có thuộc đồ hàm số vừa tìm được hay không?
c) Tìm \(m\) để đồ thị hàm số đi qua điểm có tọa độ \(\left( {{x_0};{y_0}} \right)\), biết \(\left( {{x_0};{y_0}} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}3x + 2y = 3\\2x + y = 1\end{array} \right.\).
d) Vẽ đồ thị hàm số với các giá trị \(m\) vừa tìm được ở phần a), b) trên cùng một mặt phẳng tọa độ.
Cho phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 3m - 2 = 0\) (1) với \(m\) là tham số.
a) Giải phương trình (1) khi \(m = 3.\)
b) Tìm giá trị của \(m\) để phương trình có nghiệm.
c) Tìm giá trị của \(m\) để phương trình (1) có hai nghiệm phân biệt \({x_1};{x_2}\) sao cho:
\(A = 2018 + 3{x_1}{x_2} - x_1^2 - x_2^2\) đạt giá trị nhỏ nhất.
1. Trong mặt phẳng tọa độ \(Oxy,\) cho điểm \(A\left( {3;\,\,3} \right)\) và \(B\left( { - 3\sqrt 2 ;\,\,0} \right).\) Hỏi phép quay ngược chiều tâm \(O\) biến điểm \(A\) thành điểm \(B\) có góc quay bằng bao nhiêu độ?
2. Cho hình vẽ bên.
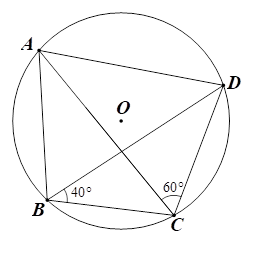
Tính số đo góc \(ADC\) bằng bao nhiêu độ?
Cho đường tròn tâm \(I\) nội tiếp tam giác \[ABC\] tiếp xúc với \[AB,{\rm{ }}AC\] lần lượt tại \[F\] và \[E.\] Kẻ \[CK\] vuông góc với \[BI.\] Chứng minh rằng:
a) Tứ giác \(AEIF\) là tứ giác nội tiếp.
b) \(\widehat {AIF} = \widehat {KIC}\) và ba điểm \[F,{\rm{ }}E,{\rm{ }}K\] thẳng hàng.








