Bộ 10 đề thi cuối kì 2 Toán 9 Chân trời sáng tạo có đáp án (Đề số 4)
20 câu hỏi
A. Trắc nghiệm
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn
Trong các hàm số sau, hàm số nào đồng biến trên \(\mathbb{R}?\)
\(y = - 3x + 2\).
\(y = \frac{{1 - x}}{2}\).
\(y = \frac{x}{3} - 1\).
\(y = 1 - 2x\).
Cho hàm số \[y = \left( {3m + 2} \right){x^2}\] với \(m = - \frac{2}{3}.\) Giá trị của tham số \[m\] để đồ thì hàm số đã cho đi qua điểm \[\left( { - 1\,;\,\,2} \right)\] là
\(m = - \frac{2}{3}.\)
\(m = 0.\)
\(m = - 1.\)
\(m = 1.\)
Cho phương trình \[a{x^2} + bx + c = 0\,\,\,\left( {a \ne 0} \right)\] có biệt thức \(\Delta = {b^2} - 4ac\). Phương trình đã cho vô nghiệm khi
\(\Delta < 0\).
\(\Delta > 0\).
\(\Delta \ge 0\).
\(\Delta \le 0\).
Phương trình nào sau đây có hai nghiệm trái dấu?
\[{x^2} - 6x + 5 = 0\].
\[{x^2} - 5x + 6 = 0\].
\[ - {x^2} - 5x - 6 = 0\].
\[{x^2} - 5x - 6 = 0\].
Biểu đồ tần số dạng cột là
biểu đồ đoạn thẳng với trục ngang biểu diễn tần số.
biểu đồ cột với trục ngang biểu diễn tần số.
biểu đồ đoạn thẳng với trục đứng biểu diễn tần số.
biểu đồ cột với trục đứng biểu diễn tần số.
Cho bảng khảo sát về chiều cao học sinh trong lớp như sau:
Chiều cao (cm) | \(\left[ {150\,;\,\,160} \right)\) | \(\left[ {160\,;\,\,167} \right)\) | \(\left[ {167\,;\,\,170} \right)\) | \(\left[ {170\,;\,\,175} \right)\) | \(\left[ {175\,;\,\,180} \right)\) |
Số học sinh | \(12\) | \(18\) | \(8\) | \(3\) | \(1\) |
Bảng số liệu ghép nhóm trên có số nhóm số liệu là
\[40\].
\[4\].
\[5\].
\[6\].
Số lượng đôi giày thể thao bán được của một cửa hàng trong bốn năm gần đây được biểu diễn ở biểu đồ sau đây:
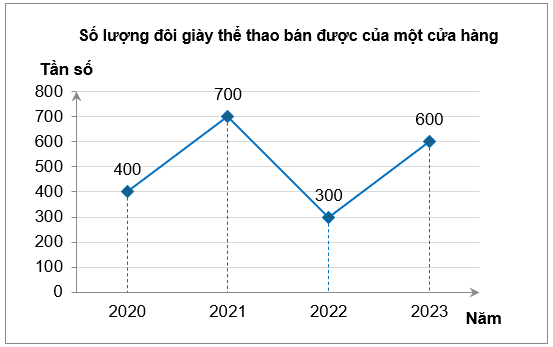
Số đôi giày cửa hàng đã bán được vào năm 2023 là
400.
600.
700.
300.
Khi gieo hai con xúc xắc cân đối và đồng chất, gọi \[T\] là tổng số chấm trên hai con xúc xắc thì kết quả nào sau đây không thể xảy ra?
\[T = 1\].
\[T = 2.\]
\[T = 3.\]
\[T = 4.\]
Tâm đường tròn nội tiếp của một tam giác là giao của các đường
trung trực.
phân giác trong.
phân giác ngoài.
đường cao.
Cho các hình vẽ sau:

Trong các hình trên, hình nào đang nội tiếp đường tròn?
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Phép quay giữ nguyên mọi điểm là phép quay
\(0^\circ \).
\(360^\circ \).
Cả A và B đều đúng.
Cả A và B đều sai.
Cho tam giác \[ABC\] đều nội tiếp đường tròn \[\left( O \right).\] Các phép quay giữ nguyên tam giác \[ABC\] là
\[\alpha _1^o = \frac{{360^\circ }}{3} = 120^\circ ;\,\,\alpha _2^o = \frac{{3 \cdot 360^\circ }}{3} = 360^\circ ;\,\,\alpha _3^o = \frac{{2 \cdot 360^\circ }}{3} = 240^\circ .\]
\[\alpha _1^o = \frac{{2 \cdot 360^\circ }}{3} = 240^\circ ;\,\,\alpha _2^o = \frac{{360^\circ }}{3} = 120^\circ ;\,\,\alpha _3^o = \frac{{3 \cdot 360^\circ }}{3} = 360^\circ .\]
\[\alpha _1^o = \frac{{360^\circ }}{3} = 120^\circ ;\,\,\alpha _2^o = \frac{{2 \cdot 360^\circ }}{3} = 240^\circ ;\,\,\alpha _3^o = \frac{{3 \cdot 360^\circ }}{3} = 360^\circ .\]
\[\alpha _1^o = \frac{{3 \cdot 360^\circ }}{3} = 360^\circ ;\,\,\alpha _2^o = \frac{{2 \cdot 360^\circ }}{3} = 240^\circ ;\,\,\alpha _3^o = \frac{{360^\circ }}{3} = 120^\circ .\]
Phần 2. Câu trắc nghiệm đúng sai
Cho phương trình \({x^2} + \left( {m + 2} \right)x + m - 1 = 0\).
a) Phương trình đã cho là phương trình bậc hai một ẩn.
b) Phương trình luôn có hai nghiệm \({x_1},\,{x_2}\) với mọi \(m.\)
c) Tổng và tích hai nghiệm của phương trình lần lượt là \({x_1} + {x_2} = m + 2\,;\,\,{x_1}{x_2} = m - 1.\)
d) Không có giá trị của \(m\) để phương trình có hai nghiệm \({x_1},\,{x_2}\) thoả mãn \({x^2}_1 - {x_1} + {x^2}_2 - {x_2} = 6.\)
Một chiếc kem ốc quế có dạng hình nón với phần vỏ quế có đường kính đáy là \[4,4{\rm{ cm,}}\] chiều cao vỏ quế \[12{\rm{ cm}}\,{\rm{.}}\] Người ta lấy phần kem từ một hộp hình trụ có chiều cao là \[15{\rm{ cm}}\] với diện tích đáy \(100\pi \,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\) để cho vào vỏ ốc quế (coi phần vỏ kem có độ dày không đáng kể).

a) Thể tích hình trụ có bán kính đáy \(R\) và chiều cao \(h\), được tính bằng công thức: \(V = \frac{1}{3}\pi {R^2}h.\)
b) Bán kính đáy của chiếc kem ốc quế là \(R = 2,2\,\,{\rm{cm}}\,{\rm{.}}\)
c) Thể tích của chiếc kem là \(\frac{{1452}}{{25}}\pi \,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right).\)
d) Ta có thể lấy kem từ hộp làm được tối đa 75 chiếc kem ốc quế.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn
Theo kế hoạch 2 tổ phải sản xuất 700 sản phẩm. Nhưng do tổ 1 làm vượt mức 15% và tổ 2 vượt mức 20% so với kế hoạch nên cả 2 tổ làm được 820 sản phẩm. Tính số sản phẩm mỗi tổ phải làm theo kế hoạch?
Tập hợp \[A\] gồm các số có ba chữ số, trong đó có 15 số nguyên tố. Bạn An chọn ngẫu nhiên một số từ tập hợp \[A.\] Biết rằng xác suất của biến cố “Chọn được số là hợp số” là \[0,7.\] Hỏi tập hợp \[A\] có bao nhiêu phần tử?
Cho tứ giác nội tiếp \(ABCD\) đường tròn \(\left( O \right)\). Hai đường thẳng \(AB\) và \(DC\) cắt nhau tại \(X.\) Biết \(\widehat {BAD} = 70^\circ ;\,\,\widehat {ABC} = 130^\circ .\) Tính số đo góc \(BXC\) (đơn vị độ).
Một chiếc nón ông già Noel thường gồm có ba phần: Hình trụ để làm đế nón, phần mũ chính là hình nón, trên đỉnh nón là quả bóng trắng có hình cầu và có các kích thước tương ứng như hình vẽ. Tính tổng diện tích phần vải để may nón, biết rằng chiều cao của đế nón bằng đường kính của quả bóng (kết quả làm tròn đến hàng đơn vị với đơn vị \[{\rm{c}}{{\rm{m}}^2}).\]
B. Tự luận
1. Biểu đồ dưới đây biểu diễn tỉ lệ về cân nặng của các bạn học sinh lớp 9A (đơn vị: kg).
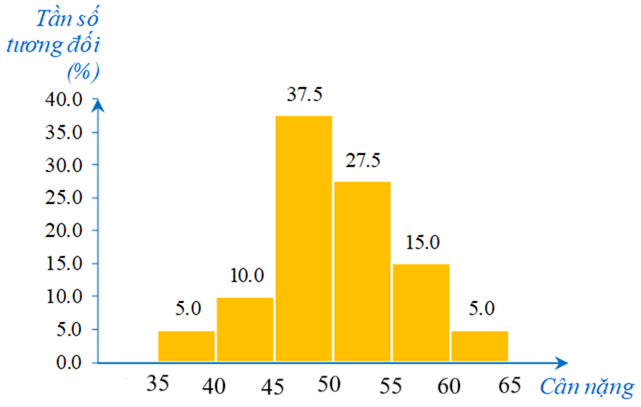
Biết rằng có 11 học sinh có cân nặng từ 50 kg đến dưới 55 kg.
a) Lập bảng tần số ghép nhóm tương ứng.
b) Bạn lớp trưởng cho rằng có trên 50% số học sinh của lớp có cân nặng từ 50 kg trở lên. Nhận định đó đúng hay sai? Tại sao?
2. Một hộp có 52 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số \[1,{\rm{ }}2,{\rm{ }}3, \ldots ,{\rm{ }}51,{\rm{ }}52;\] hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tìm số phần tử của tập hợp C gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra. Sau đó, hãy tính xác suất của mỗi biến cố “Số xuất hiện trên thẻ được rút ra là số khi chia cho 4 và 5 đều có số dư là 1”.
Cho đường tròn \(\left( O \right)\), bán kính \(R\,\,\left( {R > 0} \right)\) và dây cung \(BC\) cố định. Một điểm \(A\) chuyển động trên cung lớn \(BC\) sao cho tam giác \(ABC\) có ba góc nhọn. Kẻ các đường cao \(AD,\,\,BE\) của tam giác \(ABC\) cắt nhau tại \(H\) và \(BE\) cắt đường tròn \(\left( O \right)\) tại \(F\)\(\left( F \right.\) khác \(\left. B \right).\)
a) Chứng minh rằng tứ giác \(DHEC\) nội tiếp.
b) Kẻ đường kính \(AM\) của đường tròn \(\left( O \right)\) và \(OI\) vuông góc với \(BC\) tại \(I\). Chứng minh \(I\) là trung điểm của \(HM\) và tính \[AF\] biết \(BC = R\sqrt 3 .\)
c) Khi \(BC\) cố định, xác định vị trí của \(A\) trên đường tròn \(\left( O \right)\) để \(DH \cdot DA\) lớn nhất.








