Bộ 10 đề thi cuối kì 2 Toán 9 Chân trời sáng tạo có đáp án (Đề số 3)
19 câu hỏi
A. Trắc nghiệm
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn
Điểm đối xứng với điểm \(\left( {x\,;\,\,y} \right)\) qua trục \(Oy\)là
\(\left( {0\,;\,\,0} \right).\)
\(\left( { - x\,;\,\,y} \right).\)
\(\left( {x\,;\,\,y} \right).\)
\[\left( {x\,;\,\, - y} \right).\]
Đồ thị các hàm số \[y = 2x\] và \[y = - \frac{{{x^2}}}{2}\] cắt nhau tại các điểm
\(\left( { - \,4\,;\,\, - 8} \right)\).
\(\left( {0\,;\,\, - 4} \right)\).
\(\left( {0\,;\,\,0} \right)\) và \(\left( { - \,4\,;\,\, - 8} \right)\).
\(\left( {0\,;\,\,0} \right)\).
Phương trình nào dưới đây là phương trình bậc hai một ẩn?
\({x^4} - 2{x^2} = 0.\)
\({x^3} + 3 = 0.\)
\(2x - 3 = 0.\)
\({x^2} - 2x - 3 = 0.\)
Hai số có tổng bằng 23 và tích của chúng bằng 120 là nghiệm của phương trình nào?
\({x^2} - 23x + 120 = 0\).
\({x^2} + 23x + 120 = 0\).
\({x^2} - 120x + 23 = 0\).
\[{x^2} + 120x + 23 = 0\].
Số đo cung tương ứng của hình quạt biểu diễn tần số tương đối \[{f_3} = 20\% \] là
\[27^\circ .\]
\[74^\circ .\]
\[36^\circ .\]
\[72^\circ .\]
Bảng phân bố tần số sau đây ghi lại số vé không bán được trong 62 buổi chiếu phim:
Lớp | \[\left[ {0\,;\,\,5} \right)\] | \[\left[ {5\,;\,\,10} \right)\] | \[\left[ {10\,;\,\,15} \right)\] | \[\left[ {15\,;\,\,20} \right)\] | \[\left[ {20\,;\,\,25} \right)\] | \[\left[ {25\,;\,\,30} \right)\] |
Tần số | 3 | 8 | 15 | 18 | 12 | 6 |
Hỏi có bao nhiêu buổi chiếu phim có nhiều nhất 19 vé không bán được?
42.
43.
44.
45.
Biểu đồ hình quạt tròn bên biểu diễn tỉ lệ người thuộc các nhóm máu ở Việt Nam. Hỏi số người thuộc nhóm máu nào ở Việt Nam chiếm tỉ lệ nhiều nhất?
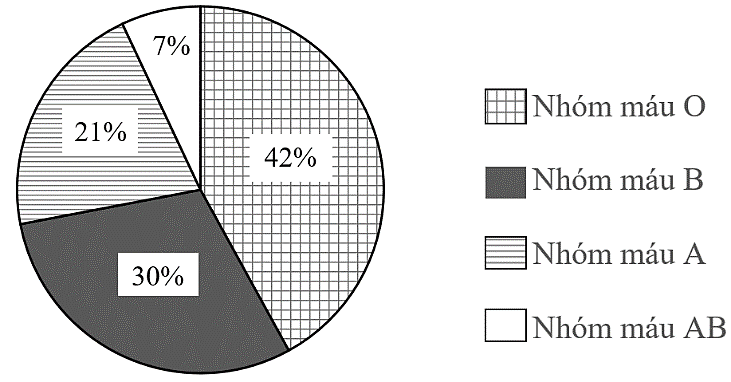
Nhóm máu \(O\).B. Nhóm máu \(B\).
Nhóm máu \(A\).D. Nhóm máu \(AB.\)
Rút ra một lá bài từ bộ bài 52 lá. Xác suất để được lá bích là
\(\frac{1}{{13}}\).
\(\frac{1}{4}\).
\(\frac{{12}}{{13}}\).
\(\frac{3}{4}\).
Đường tròn nội tiếp hình vuông cạnh \[a\] có bán kính là
\(a\sqrt 2 \).
\(\frac{{a\sqrt 2 }}{2}\).
\(\frac{a}{2}\).
\(\frac{{a\sqrt 3 }}{2}\).
Khi tứ giác \[MNPQ\] nội tiếp đường tròn, và có \(\widehat M = 90^\circ \). Khi đó, góc \[P\] bằng
\(90^\circ \).
\(180^\circ \).
\(110^\circ \).
\(120^\circ \).
Cho ngũ giác đều \[MNPQR\] có tâm \[O.\] Phép quay nào với tâm \[O\] biến ngũ giác đều \[MNPQR\] thành chính nó?
\[60^\circ .\]
\[72^\circ .\]
\[90^\circ .\]
\[120^\circ .\]
Phần 2. Câu trắc nghiệm đúng sai
Cho phương trình \(2{x^2} + \left( {2m - 1} \right)x + m - 1 = 0\) với \(m\) là tham số, \(m \ne \frac{3}{2}.\)
a) Phương trình đã cho là phương trình bậc hai một ẩn.
b) Phương trình luôn có hai nghiệm \({x_1},\,{x_2}\) với mọi \(m \ne \frac{3}{2}.\)
c) Tổng và tích hai nghiệm của phương trình lần lượt là \({x_1} + {x_2} = \frac{{2m - 1}}{2};\,\,{x_1}{x_2} = \frac{{m - 1}}{2}.\)
d) Có một giá trị của \(m\) để phương trình có hai nghiệm \({x_1},\,{x_2}\) thoả mãn \[4x_1^2 + 2{x_1}{x_2} + 4x_2^2 = 1.\]
Cho hình bên là một thúng gạo vun đầy. Thúng có dạng nửa hình cầu với đường kính \[50\,\,{\rm{cm,}}\] phần gạo vun lên có dạng hình nón cao \[15\,\,{\rm{cm}}{\rm{.}}\]

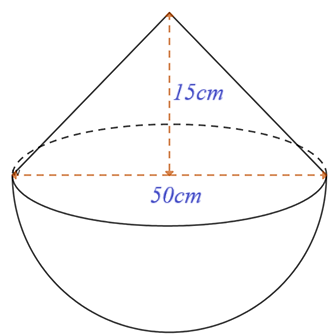
Nhà Danh dùng lon sữa bò cũ có dạng hình trụ (bán kính đáy bằng \[5\,\,{\rm{cm}},\] chiều cao \[15\,\,{\rm{cm}})\] để đong gạo mỗi ngày. Biết mỗi ngày nhà Danh ăn 5 lon gạo và mỗi lần đong thì lượng gạo chiếm \[90\% \] thể tích lon.
a) Thể tích hình cầu có bán kính đáy \(R\), được tính bằng công thức: \(V = \frac{4}{3}\pi {R^3}.\)
b) Phần gạo nằm ngang mặt thúng trở xuống có dạng nửa hình cầu có bán kính \[50\,\,{\rm{cm}}\].
c) Thể tích phần gạo trong thúng là \(\frac{{60\,\,625}}{3}\pi \,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right).\)
d) Với lượng gạo ở thúng trên thì nhà Danh có thể ăn nhiều nhất là 15 ngày.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn
Một ô tô khách và một ô tô tải chở vật liệu xây dựng khởi hành cùng một lúc từ bến xe khách Lai Châu đến trung tâm thị trấn Mường Tè. Do trọng tải lớn nên xe tải chở vật liệu xây dựng đi với vận tốc chậm hơn xe khách \(10\,\,{\rm{km/h}}.\) Xe khách đến trung tâm thị trấn Mường Tè sớm hơn xe tải 1 giờ 6 phút. Biết quãng đường từ bến xe khách thành phố Lai Châu đến trung tâm thị trấn Mường Tè là \[132\,\,{\rm{km}}.\]Tính vận tốc của xe tải (theo đơn vị \({\rm{km/h}})\).
Một hộp đựng 3 quả bóng màu đỏ và 2 quả bóng màu vàng có cùng kích thước, khối lượng. Lấy ngẫu nhiên hai quả bóng trong hộp. Tính xác suất để hai quả bóng lấy ra cùng màu (viết kết quả dưới dạng số thập phân).
Người ta làm một khung gỗ hình tam giác đều đặt vừa khít một chiếc đồng hồ hình tròn có đường kính \[40{\rm{ cm}}.\] Độ dài các cạnh (phía bên trong) của khung gỗ phải bằng bao nhiêu (làm tròn kết quả đến hàng đơn vị với đơn vị \[{\rm{cm}}\])?
![Người ta làm một khung gỗ hình tam giác đều đặt vừa khít một chiếc đồng hồ hình tròn có đường kính \[40{\rm{ cm}}.\] Độ dài các cạnh (phía bên trong) của khung gỗ phải bằng bao nhiêu (làm trò (ảnh 1)](https://video.vietjack.com/upload2/images/1741014141/1741014919-image8.png)
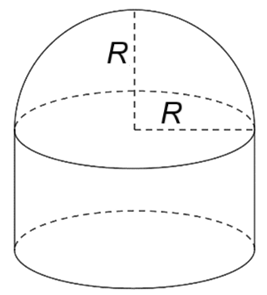
Một chụp nhựa bảo vệ chuông điện có cấu trúc gồm một phần là hình trụ bán kính đáy \(R\), chiều cao \(6\,\,{\rm{cm}}\) và một phần là hình bán cầu bán kính \(R\) (như hình vẽ). Cho biết diện tích mặt xung quanh của khối chụp là \(120\pi \,\,{\rm{c}}{{\rm{m}}^{\rm{2}}}.\) Tính thể tích khối chụp (kết quả làm tròn đến hàng đơn vị với đơn vị \[{\rm{c}}{{\rm{m}}^{\rm{3}}}).\]
B. Tự luận
1. Ghi lại cự li ném tạ (đơn vị: mét) của một vận động viên sau đợt tập huấn đặc biệt trong bảng sau:
20 | 20,5 | 20,64 | 20,35 | 20,65 | 20,4 | 20,67 | 20,8 |
20,7 | 20,45 | 20,72 | 20,5 | 20,85 | 20,2 | 21,1 | 20,9 |
a) Để thu gọn bảng dữ liệu trên thì nên chọn bảng tần số ghép nhóm hay tần số không ghép nhóm? Vì sao?
b) Hãy lập bảng số liệu làm 6 nhóm trong đó nhóm đầu tiên cự li là từ 20 đến dưới 20,2 m. Lập bảng tần số và tần số tương đối ghép nhóm.
2. Một hộp có \[52\] chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số \(1;\,\,2;\,\,3;\,\,4;\,\,...\,\,;\,\,51;\,\,52\) hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố \(A\): “Số xuất hiện trên thẻ được rút ra là số nhỏ hơn \[27\]”.
Cho tam giác \[ABC\] nhọn có \[AB < AC\] nội tiếp đường tròn \[\left( {O;R} \right)\]. Các đường cao \[BE;\,\,CF\] của tam giác cắt nhau tại \[H\] \[\left( E \right.\] thuộc \[AC,\,\,F\]thuộc \[\left. {AB} \right).\]
a) Chứng minh: Tứ giác \[BFEC\] nội tiếp đường tròn.
b) Kẻ đường kính \[AK\] của đường tròn \[\left( O \right)\]. Chứng minh \[AK\] vuông góc với \[EF\].
c) Giả sử \[BC\] cố định và \[A\] di chuyển trên cung lớn \[BC\] sao cho tam giác\[ABC\] luôn là tam giác nhọn. Xác định vị trí của điểm \[A\] để diện tích tam giác \[EAH\] lớn nhất. Tính giá trị lớn nhất đó theo \[R\] khi \[BC = R\sqrt 3 .\]








