Bộ 10 đề thi cuối kì 2 Toán 9 Chân trời sáng tạo có đáp án (Đề số 2)
20 câu hỏi
A. Trắc nghiệm
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn
Giá trị của \[m\] để hàm số \[y = \left( {2 - m} \right){x^2}\,\,\left( {m \ne 2} \right)\] nghịch biến với mọi giá trị của \[x > 0\] là
\[m < - 2\].
\[m < 2\].
\[m > - 2\].
\[m > 2\].
Cho parabol \(\left( P \right):\,y\, = \,\frac{1}{2}{x^2}\) và đường thẳng \(\left( d \right):\,y\, = \,x\, - \,\frac{1}{2}\). Tọa độ giao điểm của đường thẳng \(\left( d \right)\) và parabol \(\left( P \right)\) là
\(\left( {1\,;\,\,\frac{1}{2}} \right)\).
\(\left( {1\,;\,\,2} \right)\).
\(\left( {\frac{1}{2}\,;\,\,\,1} \right)\).
\(\left( {2\,;\,\,\,1} \right)\).
Cho phương trình \[a{x^2} + bx + c = 0\,\,\,\left( {a \ne 0} \right)\] có biệt thức \(\Delta = {b^2} - 4ac\). Phương trình đã cho vô nghiệm khi
\(\Delta < 0\).
\(\Delta > 0\).
\(\Delta \ge 0\).
\(\Delta \le 0\).
Hai số \(u,\,v\) có tổng và tích lần lượt là 32 và 231. Khi đó \(u\) và \(v\) là nghiệm của phương trình nào dưới đây?
\({x^2} - 231x - 32 = 0.\)
\({x^2} + 32x + 231 = 0.\)
\({x^2} - 32x + 231 = 0.\)
\({x^2} + 231x + 32 = 0.\)
Công thức tính giá trị đại diện của nhóm \[\left[ {{a_i};{a_{i + 1}}} \right)\] là
\[{x_i} = {a_{i + 1}} - {a_i}.\]
\[{x_i} = {a_{i + 1}} + {a_i}.\]
\[{x_i} = \frac{{{a_i} + {a_{i + 1}}}}{2}.\]
\[{x_i} = \frac{{{a_i} - {a_{i + 1}}}}{2}.\]
Cho bảng tần số ghép nhóm:
Nhóm | \[\left[ {7\,;\,\,13} \right)\] | \[\left[ {13\,;\,\,19} \right)\] | \[\left[ {19\,;\,\,25} \right)\] | \[\left[ {25\,;\,\,31} \right)\] |
\[\]Tần số | \(5\) | \[10\] | \[20\] | \[15\] |
Mệnh đề sai là mệnh đề
Tần số của nhóm là \[15\].
Tần số tương đối ghép nhóm của nhóm \[\left[ {7\,;\,\,13} \right)\] là \[10\% \].
Tần số tương đối ghép nhóm của nhóm \[\left[ {13\,;\,\,19} \right)\] là \[20\% \].
Tần số tương đối ghép nhóm của nhóm \[\left[ {19\,;\,\,25} \right)\] là \[30\% \].
Trong một kỳ thi học sinh giỏi Toán (thang điểm 20) của 50 học sinh, kết quả được cho bởi
biểu đồ sau:
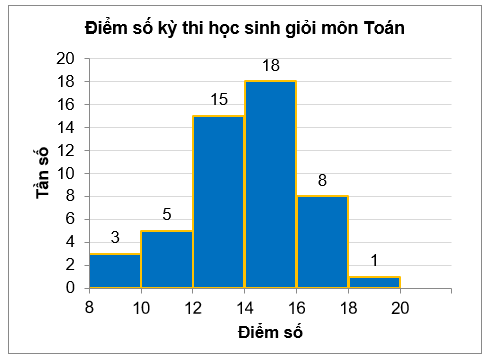
Tần số của nhóm thí sinh có điểm thi thấp nhất là
1.
3.
5.
18.
Thống kê thời gian của 78 chương trình quảng cáo trên Đài truyền hình tỉnh X có 38 chương trình quảng cáo từ 10 đến 17 giây. Xác suất thực nghiệm của biến cố trên là
\(\frac{1}{{78}}\).
\(\frac{{38}}{{78}}\).
\(\frac{5}{{78}}\).
\(\frac{4}{{78}}\).
Khẳng định nào sau đây là sai?
Trọng tâm của tam giác đều vừa là tâm đường tròn ngoại tiếp, vừa là tâm đường tròn nội tiếp tam giác đều đó.
Tâm đường tròn nội tiếp tam giác là giao điểm của ba đường phân giác của tam giác đó.
Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.
Đường tròn ngoại tiếp một tam giác là đường tròn đi qua nhiều nhất là ba đỉnh của tam giác đó.
Góc nội tiếp nhỏ hơn hoặc bằng \(90^\circ \) có số đo
bằng nửa số đo góc ở tâm cùng chắn một cung.
bằng số đo của góc ở tâm cùng chắn một cung.
bằng số đo cung bị chắn.
bằng nửa số đo cung lớn.
Khi quay thuận chiều \(\alpha ^\circ \) tâm \[O\] điểm \[A\] thành điểm \[B\] thì điểm \[A\] tạo thành cung \[AB\] có số đo bằng
\(90^\circ - \alpha ^\circ \) .
\[ - \alpha ^\circ \].
\(\alpha ^\circ \).
\(180^\circ - \alpha ^\circ \).
Số cạnh của đa giác đều có số đường chéo bằng số cạnh là
5.
6.
7.
8.
Phần 2. Câu trắc nghiệm đúng sai
Cho phương trình \(2{x^2} - 3x + 1 = 0.\)
a) Phương trình đã cho có hệ số \(a = 2\,;\,\,b = 3\,;\,\,c = 1.\)
b) Tổng các hệ số \(a,\,\,b,\,\,c\) là 0.
c) Phương trình đã cho có hai nghiệm đều dương.
d) Tích hai nghiệm của phương trình đã cho là 1.
Một cái ly thủy tinh (như hình vẽ), phần phía trên là hình nón có chiều cao \[7\,{\rm{cm,}}\] có đáy đường tròn bán kính \[4\,\,{\rm{cm}}{\rm{.}}\] Biết trong ly đang chứa rượu với mức rượu đang cách miệng ly là \[3\,\,{\rm{cm}}.\]

a) Thể tích hình nón có bán kính đáy \(R\) và chiều cao \(h\), được tính bằng công thức: \(V = \pi {R^2}h.\)
b) Chiều cao của phần rượu có trong ly là \[4\,\,{\rm{cm}}.\]
c) Thể tích của cái ly thủy tinh là \[\frac{{28}}{3}\pi \,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}{\rm{.}}\]
d) Tỉ số giữa thể tích của phần còn lại trong ly rượu so với thể tích ly là \[\frac{4}{7}\].
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn
Để chở 15 tấn thiết bị phục vụ Lễ kỷ niệm 70 năm chiến thắng Điện Biên Phủ, một đội vận chuyển dự định sử dụng các xe tải loại nhỏ. Do thay đổi kế hoạch, đội vận chuyển quyết định chỉ sử dụng các xe tải loại lớn. Vì vậy, số xe sử dụng giảm đi hai xe so với dự định và mỗi xe tải loại lớn chở nhiều hơn mỗi xe tải loại nhỏ là 2 tấn. Biết mỗi xe tải cùng loại đều chở số tấn thiết bị bằng nhau. Hỏi đội vận chuyển sử dụng bao nhiêu xe tải loại lớn?
Một hộp chứa 4 tấm thẻ cùng loại được đánh số 1;4;7;9 Bạn Khuê và bạn Hương lần lượt mỗi người lấy ra 1 tấm thẻ từ hộp. Tính xác suất của biến cố \(A:\) “Số ghi trên tấm thẻ của bạn Khuê nhỏ hơn số ghi trên tấm thẻ của bạn Hương” (viết kết quả dưới dạng số thập phân).
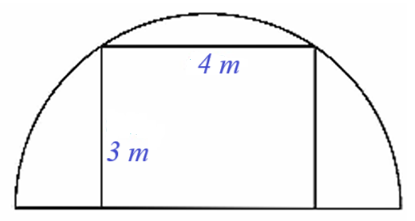
Người ta cần xây dựng một khung cổng hình chữ nhật rộng \[4{\rm{ m}}\] và cao \[3{\rm{ m,}}\] bên ngoài khung cổng được bao bởi một khung thép dạng nửa hình tròn (như hình vẽ). Chiều dài của đoạn thép dùng để làm khung nửa đường tròn đó là bao nhiêu? (làm tròn kết quả đến hàng phần mười).
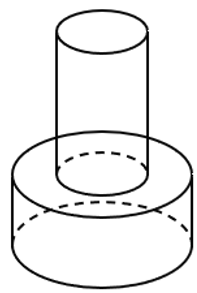
Một khối đồ chơi gồm hai khối trụ \(\left( {{H_1}} \right)\), \(\left( {{H_2}} \right)\) xếp chồng lên nhau, lần lượt có bán kính đáy và chiều cao tương ứng là \({r_1}\), \({h_1}\), \({r_2}\), \({h_2}\) thỏa mãn \({r_2} = \frac{1}{2}{r_1}\), \({h_2} = 2{h_1}\) (tham khảo hình vẽ). Biết rằng thể tích của toàn bộ khối đồ chơi bằng \(30{\rm{ c}}{{\rm{m}}^3}.\) Tính thể tích khối trụ \(\left( {{H_1}} \right)\).
B. Tự luận
1. Kết quả nhảy xa của một lớp (đơn vị mét) được cho trong bảng sau:
2,4 | 3,1 | 2,7 | 2,8 | 3,2 | 2,8 | 4,1 | 3,2 |
2,1 | 3,2 | 2,1 | 3,2 | 2,3 | 2,5 | 2,6 | 3,3 |
3,6 | 2,0 | 2,0 | 2,7 | 3,1 | 2,3 | 4,3 | 3,9 |
3,9 | 3,5 | 3,6 | 3,7 | 2,7 | 3,5 | 3,5 | 2,4 |
a) Để thu gọn bảng dữ liệu trên thì nên chọn bảng tần số ghép nhóm hay tấn số không ghép nhóm? Vì sao?
b) Hãy lập bảng số liệu làm 5 nhóm trong đó nhóm cuối cùng cự li là từ 4,0 đến dưới 4,5 m. Lập bảng tần số và tần số tương đối ghép nhóm.
2. Cho hai túi I và II mỗi túi chứa 3 tấm thẻ được đánh số \[2\,;\,\,3\,;\,\,4.\] Rút ngẫu nhiên từ mỗi túi ra 1 tấm thẻ và ghép thành số có hai chữ số với chữ số trên tấm thẻ rút từ túi I là chữ số hàng chục. Tính xác suất của biến cố “Số tạo thành là số chia hết cho 3”.
Cho đường tròn \(\left( {O;\,\,R} \right)\). Từ \(A\) trên \(\left( O \right),\) kẻ tiếp tuyến \(d\) với \(\left( O \right).\) Trên đường thẳng \(d\) lấy điểm \(M\) bất kỳ \(\left( M \right.\) khác \(\left. A \right),\) kẻ cát tuyến \(MNP.\) Gọi \(K\) là trung điểm của \(NP,\) kẻ tiếp tuyến \(MB\). Kẻ \[AC \bot MB,\,\,BD \bot AM\,\,\left( {C \in MB,\,\,D \in AM} \right).\] Gọi\[H\] là giao điểm của \[AC\] và \[BD,\] \[I\] là giao điểm của \[OM\] và \[AB.\]
a) Chứng minh tứ giác \(AMBO\) nội tiếp.
b) Chứng minh \(OI \cdot OM = {R^2}\) và \(OI \cdot IM = I{A^2}\).
c) Chứng minh ba điểm \(O,\,\,H,\,\,M\) thẳng hàng.








