54 bài tập Hàm số bậc hai và giải bài toán bằng cách lập phương trình có lời giải

Một hòn đá rơi xuống một cái hang, khoảng cách rơi xuống h (tính bằng mét) được cho bởi công thức \({\rm{h}} = 9,8.{{\rm{t}}^2}\), trong đó t là thời gian rơi (tính bằng giây).
a) Hãy tính độ sâu của hang nếu mất 3 giây để hòn đá chạm đáy.
b) Nếu hang sâu 156,8 mét thì phải mất bao lâu để hòn đá chạm tới đáy.

Lực \(F\) (tính bằng đơn vị N ) của gió thổi vào cánh buồm tỷ lệ với vận tốc của gió \(({\rm{km}}/{\rm{h}})\) bằng công thức \(F = k.{v^2}\). Biết nếu vận tốc của gió là \(5\;{\rm{km}}/{\rm{h}}\) thì lực của gió thổi vào cánh buồm là 100 N.
a) Tìm hệ số \(k\).
b) Cánh buồm chỉ chịu được lực tối đa là 3000 N. Hỏi nếu vận tốc gió là \(30\;{\rm{km}}/{\rm{h}}\) thì thuyền có thể ra khơi
được không?

Biết rằng nhiệt lượng tỏa ra trên dây dẫn được tính bởi công thức: \({\rm{Q}} = 0,24{\rm{R}}{{\rm{I}}^2}{\rm{t}}\). Trong đó \(Q\) là nhiệt lượng tính bằng \({\rm{J}},{\rm{R}}\) là điện trở tính bằng ôm \((\Omega )\), I là cường độ dòng điện tính bằng ampe \(({\rm{A}}),{\rm{t}}\) là thời gian tính bằng giây \(({\rm{s}})\). Dòng điện chạy qua một dây dẫn có điện trở \({\rm{R}} = 10\Omega \) trong thời gian 5 giây. Tính cường độ dòng điện khi nhiệt lượng tỏa ra là 180 J. (Làm tròn các kết quả đến chữ số thập phân thứ hai).

Vận tốc lăn \(v\) (tính bằng \({\rm{m}}/{\rm{s}})\) của một vật thể nặng \({\rm{m}}\)(tính bằng kg ) được tác động một lực \({{\rm{E}}_{\rm{k}}}\) (gọi là năng lượng Kinetic Energy, ký hiệu \({{\rm{E}}_{\rm{k}}}\), tính bằng J ) được cho bởi công thức: \({{\rm{E}}_{\rm{k}}} = \frac{{\rm{m}}}{2}{{\rm{v}}^2}\)
a) Hãy tính vận tốc của một quả banh bowling nặng 3 kg khi một người tác động một lực \({{\rm{E}}_{\rm{k}}} = 18\;{\rm{J}}\)?
b) Muốn lăn một quả bowling nặng 3 kg với vận tốc \(6\;{\rm{m}}/{\rm{s}}\), thì cần sử dụng năng lượng Kinetic \({{\rm{E}}_{\rm{k}}}\) bao nhiêu Joule?

\({\rm{P}}\) là công suất (tính theo watt) cho một mạch điện được cho bởi công thức \({\rm{P}} = \frac{{{{\rm{V}}^2}}}{{\rm{R}}}\), trong đó điện áp V (tính theo volt) và \({\rm{R}}\) là điện trở trong (tính theo ohm).
a) Bóng đèn B có điện áp bằng 110 volt, điện trở trong là 88 ohm có công suất bao nhiêu?
b) Cần bao nhiêu volt để thắp sáng một bóng đèn A có công suất 100 watt và điện trở của mỗi bóng đèn là 80 ohm? (làm tròn các kết quả đến hàng đơn vị).

Sóng thần (tsunami) là một loạt các đợt sóng tạo nên khi một thể tích lớn của nước đại dương bị dịch chuyển chớp nhoáng trên một quy mô lớn. Động đất cùng những dịch chuyển địa chất lớn bên trên hoặc bên dưới mặt nước, núi lửa phun và va chạm thiên thạch đều có khả năng gây ra sóng thần. Con sóng thần khởi phát từ dưới đáy biển sâu, khi còn ngoài xa khơi, sóng có biên độ (chiều cao sóng) khá nhỏ nhưng chiều dài của cơn sóng lên đến hàng trăm km. Con sóng đi qua đại dương với tốc độ trung bình 500 dặm một giờ. Khi tiến tới đất liền, đáy biển trở nên nông, con sóng không còn dịch chuyển nhanh được nữa, vì thế nó bắt đầu "dựng đứng lên" có thể đạt chiều cao một tòa nhà sáu tầng hay hơn nữa và tàn phá khủng khiếp.
Chiều sâu của đại dương và tốc độ của con sóng liên hệ bởi công thức \({\rm{d = }}\frac{{{{\rm{s}}^{\rm{2}}}}}{{\rm{g}}}\). Trong đó \({\rm{g}} = 9,81\;{\rm{m}}/{{\rm{s}}^2},\)\(\;{\rm{d}}\left( {{\rm{deep}}} \right)\)là chiều sâu đại dương tính bằng\(m\),\(s\)là vận tốc của sóng thần tính bằng \({\rm{m/s}}\).
a) Biết độ sâu trung bình của đại dương trên trái đất là \({\rm{d}} = 3785\) mét hãy tính tốc độ trung bình của các con sóng thần xuất phát từ đáy các đại dương theo \({\rm{km}}/{\rm{h}}\).
b) Susan Kieffer, một chuyên gia về cơ học chất lỏng địa chất của đại học Illinois tại Mỹ, đã nghiên cứu năng lượng của trận sóng thần Tohoku 2011 tại Nhật Bản. Những tính toán của Kieffer cho thấy tốc độ sóng thần vào xấp xỉ \(225\;{\rm{m}}/{\rm{s}}\). Hãy tính độ sâu của đại dương nơi xuất phát con sóng thần này.(Làm tròn các kết quả đến chữ số thập phân thứ hai).

Một bể nước hình hộp chữ nhật có đáy hình vuông cạnh bằng \(x\) mét. Chiều cao của bể bằng 2 m. Kí hiệu \(V(x)\) là thể tích của bể.
a) Tính thể tích \(V(x)\) theo \(x\).
b) Giả sử chiều cao của bể không đổi, hãy tính \(V(1),V(2),V(3)\). Nhận xét khi \(x\) tăng lên 2 lần, 3 lần thì thể tích tương ứng của bể tăng lên mấy lần?

Sau những vụ va chạm giữa các xe trên đường, cảnh sát thường sử dụng công thức dưới đây để ước lượng tốc độ \(v\) (đơn vị: dặm/giờ) của xe từ vết trượt trên mặt đường sau khi thắng đột ngột \(d = \frac{1}{{30f}}{v^2}\). Trong đó, \(d\) là chiều dài vết trượt của bánh xe trên nền đường tính bằng feet \(({\rm{ft}}),f\) là hệ số ma sát giữa bánh xe và mặt đường (là thước đo sự "trơn trượt" của mặt đường).
Đường Cao tốc Long Thành - Dầu Giây có tốc độ giới hạn là \(100\;{\rm{km}}/{\rm{h}}\). Sau một vụ va chạm giữa hai xe, cảnh sát đo được vết trượt của một xe là \(d = 185{\rm{ft}}\) và hệ số ma sát mặt đường tại thời điểm đó là \(f = 0,73\). Chủ xe đó nói xe của ông không chạy quá tốc độ. Hãy áp dụng công thức trên để ước lượng tốc độ chiếc xe đó rồi cho biết lời nói của người chủ xe đúng hay sai? (Biết 1 dặm \( = 1609\;{\rm{m}})\). (Làm tròn các kết quả đến chữ số thập phân thứ hai).

Một quả bóng được thả rơi từ độ cao \(360m\). Khi bỏ qua sức cản của không khí, độ cao của quả bóng so với ví trí đứng thả (tính bằng mét) có thể mô tả bởi phương trình: \(s = a{t^2},a > 0\).
a) Xác định hệ số \(a\) biết sau 2 giây, bóng rơi được \(22m\).
b) Sau 5 giây, bóng cách đất bao nhiêu mét?
c) Quãng đường bóng đi được trong 2 giây cuối?

Để tính toán chiều dài của dây đu trong thời gian một chu kỳ đong đưa (một chu kỳ đong đưa dây đu được tính từ lúc dây đu bắt đầu được đưa lên cao đến khi dừng hẳn người ta sử dụng công thức: \(L = \frac{g}{{4{\pi ^2}}}{T^2}\). Trong đó, \(T\) là thời gian một chu kỳ đong đưa \(({\rm{s}}),{\rm{L}}\) là chiều dài của dây đu \((\;{\rm{m}}),{\rm{g}} = 9,81\;{\rm{m}}/{{\rm{s}}^2},\pi \approx 3,14\).
a) Một người muốn thiết kế một dây đu sao cho một chu kỳ đong đưa kéo dài 3 giây. Hỏi người đó phải làm một sợi dây đu dài bao nhiêu?
b) Một sợi dây đu có chiều dài 8 m, hỏi chu kỳ đong đưa dài bao nhiêu giây?
(Làm tròn các kết quả đến hàng đơn vị).

Với thiết kế độc đáo, cổng trường Đại học Bách Khoa Hà Nội được xây dựng cách đây khoảng 50 năm và đã từng là niềm tự hào của tri thức thế hệ mới. Chiếc cổng có chiều cao \(7,6\;{\rm{m}}\) và khoảng cách giữa hai chân cổng là \({\rm{AB}} = 9\;{\rm{m}}\). Một bạn sinh viên đứng cách chân cổng một đoạn \({\rm{AE}} = 0,5\;{\rm{m}}\) thì đỉnh đầu bạn ấy vừa chạm vào cổng. Hỏi bạn đó cao bao nhiêu.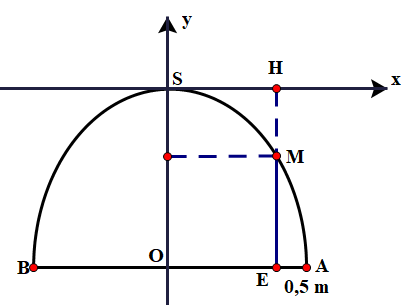

Từ lan can một tòa nhà cách mặt đất \(18m\) bạn An ném một chiếc máy bay đồ chơi theo phương ngang xuống đất. Biết máy bay rơi xuống theo quỹ đạo là một đường parabol và sau 6 giây kể từ vị trí cao nhất đó, máy bay rơi chạm mặt đất. Tìm hàm số biểu thị quỹ đạo nhảy của máy bay đồ chơi. Suy ra độ cao của máy bay sau 3 giây.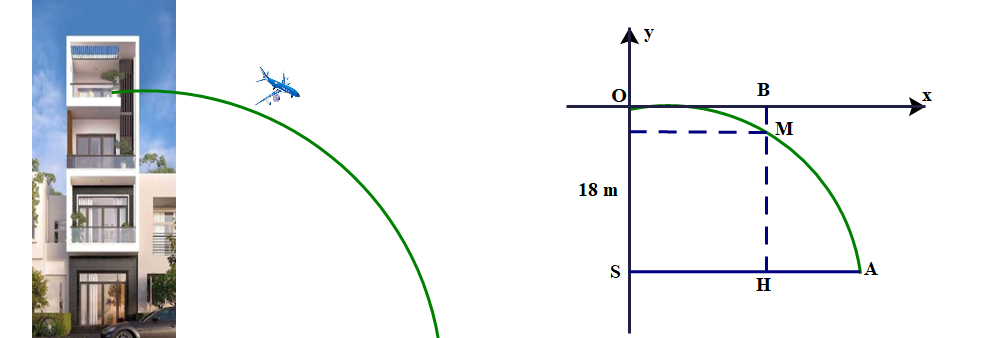

Cá heo có thể nhảy cao tới 25 feet và thực hiện các thủ thuật như nhảy qua vòng, lộn nhào trong không trung. Giả sử quỹ đạo nhảy của cá heo là parabol và sau 2 giây kể từ vị trí cao nhất đó, cá heo rơi chạm mặt nước. Tìm hàm số biểu thị quỹ đạo nhảy của cá heo. Hỏi sau mấy giây kể từ vị trí cao nhất đó thì cá heo cách mặt nước 10 feet. (kết quả làm tròn đến hàng phần chục)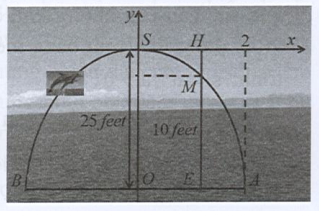

Một cây cầu treo có trọng lượng phân bố đều dọc theo chiều dài của nó. Cây cầu có trụ tháp đôi cao \(80m\) so với mặt của cây cầu và cách nhau \(440m\). Dây cáp treo có hình dạng đường parabol và được treo trên các đỉnh tháp và chạm mặt cầu ở vị trí chính giữa của cây cầu. Tìm chiều cao của dây cáp tại điểm cách điểm chính giữa của cây cầu \(130m\) (giả sử mặt của cây cầu là bằng phẳng).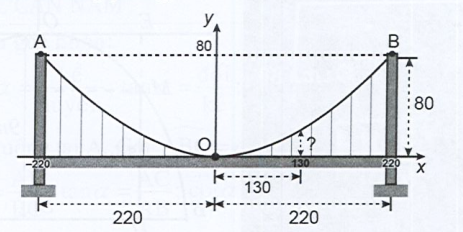

Một xe tải có chiều rộng là \(2,4\;{\rm{m}}\) chiều cao là \(2,5\;{\rm{m}}\) muốn đi qua một cái cổng hình parabol. Biết khoảng cách giữa hai chân cổng là 4 m và khoảng cách từ đỉnh cổng tới mỗi chân cổng là \(2\sqrt 5 \;{\rm{m}}\) (bỏ qua độ dày của cổng).
a) Trong mặt phẳng tọa độ \(Oxy\) gọi parabol \((P):y = a{x^2}\) với a \( < 0\) là hình biểu diễn cổng mà xe tải muốn đi qua. Chứng minh \(a = - 1\).
b) Hỏi xe tải có đi qua cổng được không? Tại sao?

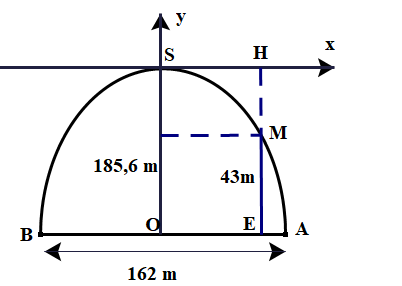
Giả sử Cổng Arch tại thành phố St Louis của Mỹ có hình dạng là một parabol (hình vẽ). Biết khoảng cách giữa hai chân cổng bằng 162 m, điểm cao nhất trên cổng cách mặt đất 185,6m. Trên thành cổng, tại vị trí có độ cao 43 m so với mặt đất (điểm M), người ta thả một sợi dây chạm đất (dây căng thẳng theo phương vuông góc với mặt đất). Hỏi vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn bao nhiêu mét? (làm tròn đến cm ) 

Ở một điểm cao trên tháp cách mặt đất \(1,75\;{\rm{m}}\) nhà thiết kế có đặt một vòi phun nước. Biết rằng đường đi của các giọt nước sau khi ra khỏi vòi có dạng đường cong parabol và lên cao nhất được \(4m\). Hỏi nước rơi xuống đất cách chân tháp bao nhiêu mét?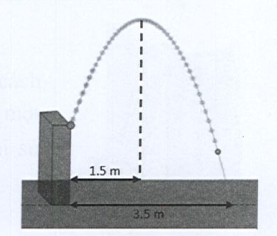

Trong một trận đấu bóng đá, người ta quan sát được quỹ đạo của quả bóng do thủ môn đá lên từ vạch\(5m50\) là một phần của đường cong parabol. Biết rằng, sau 3 giây thì quả bóng lên đến vị trí cao nhất là 9 mét (tham khảo hình vẽ). Hỏi sau mấy giây đầu tiên kể từ khi bóng được đá lên thì đạt độ cao \(5m\).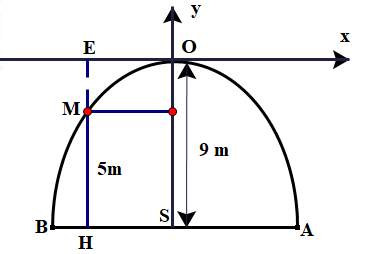

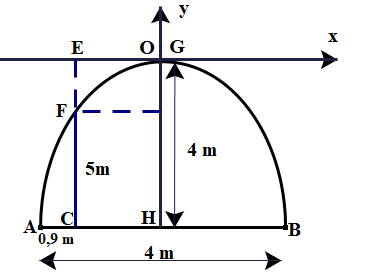
Một cái cổng hình parabol như hình vẽ. Chiều cao \({\rm{GH}} = 4\;{\rm{m}}\), chiều rộng \({\rm{AB}} = 4\;{\rm{m}}\), \({\rm{AC}} = {\rm{BD}} = 0,9\;{\rm{m}}\). Chủ nhà làm hai cánh cổng khi đóng lại là hình chữ nhật CDEF tô đậm giá là 1.200.000 đồng\(/{{\rm{m}}^2}\), còn các phần để trắng làm xiên hoa có giá là 900.000 đồng\(/{{\rm{m}}^2}\). Biết diện tích của toàn bộ cái cổng là \(\frac{{32}}{3}\;{{\rm{m}}^2}\). Tính tổng chi phí để làm cổng?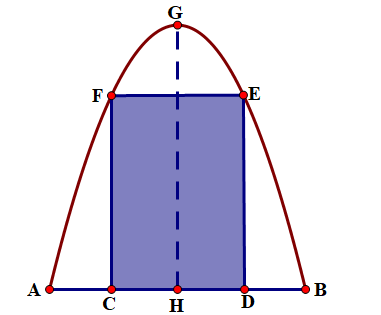 

Đạp xe là một hình thức tập thể dục đơn giản, rất tốt cho sức khỏe và thân thiện với môi trường. Sáng sớm, Mai dự định đạp xe từ nhà ra Hồ Gươm rồi lại đạp xe về để tập thể dục. Khi ra đến Hồ Gươm, bạn dừng lại nghỉ 3 phút. Do đó để về nhà đúng giờ, bạn phải tăng tốc thêm \(2\;{\rm{km/h}}\). Tính vận tốc dự định và thời gian đi xe đạp của bạn Mai. Biết quãng đường lúc đi và lúc về đều là \(3\;{\rm{km}}\).

Khoản 1 Điều 3 Nghị định 100/2019/NĐ-CP quy định tốc độ tối đa của xe đạp điện là \(25\;{\rm{km/h}}\). Hai bạn Tuấn và Minh cùng xuất phát một lúc để đến khu bảo tồn thiên nhiên trên quãng đường dài \(22\;{\rm{km}}\)bằng phương tiện xe đạp điện. Mỗi giờ Tuấn đi nhanh hơn Minh \(2\;{\rm{km}}\)nên đến nơi sớm hơn \(5\) phút. Hỏi hai bạn đi như vậy có đúng vận tốc quy định hay không?

Quãng đường Thanh Hóa – Hà Nội dài 150 km. Một ôtô từ Hà Nội vào Thanh Hóa, nghỉ lại Thanh Hóa 3 giờ 15 phút, rồi trở về Hà Nội, hết tất cả 10 giờ. Tính vận tốc của ôtô lúc về, biết rằng vận tốc lúc đi lớn hơn vận tốc lúc về là 10 km/h.

Lúc \[5\] giờ \[15\] phút, một người đi xe máy từ \[A\]đến \[B\]dài \[75\] km với vận tốc dự định. Đến\[B\], người đó nghỉ \[20\] phút rồi quay về \[A\]và đi nhanh hơn lúc đi mỗi giờ \[5\] km. Người đó về đến \[A\] lúc \[12\] giờ \[20\] phút. Tính vận tốc lúc đi của người đó.

Một người đi xe đạp từ địa điểm \(A\) đến địa điểm \(B\) cách nhau \(30{\rm{km}}\). Khi đi từ \(B\) về \(A\) người đó chọn con đường khác dễ đi hơn nhưng dài hơn con đường cũ \(6{\rm{km}}\). Vì đi với vận tốc lớn hơn vận tốc lúc đi là \(3{\rm{km/h}}\) nên thời gian về vẫn ít hơn thời gian đi là 20 phút. Tính vận tốc lúc đi.

Lúc \[6\] giờ \[30\] phút sáng, một ca nô xuôi dòng sông từ \[A\] đến \[B\] dài \[48\]km. Khi đến\[B\], ca nô nghỉ \[30\] phút sau đó ngược dòng từ \[B\] về \[A\]lúc \[10\] giờ \[36\] phút cùng ngày. Tìm vận tốc riêng của ca nô biết vận tốc dòng nước là \[3\] km/h.Cho ….

Hai ô tô cùng khởi hành từ A đến B với vận tốc của mỗi xe không đổi trên toàn bộ quãng đường \(AB\)dài \(150\)km. Do vận tốc của ô tô thứ nhất lớn hơn vận tốc của ô tô thứ hai là \(10\)km/h nên ô tô thứ nhất đến sớm hơn ô tô thứ hai \(30\)phút. Tính vận tốc mỗi ô tô.

Khoảng cách giữa hai thành phố A và B là 144 km. Một ô tô khởi hành từ thành phố A đến thành phố B với vận tốc không đổi trên cả quãng đường. Sau khi ô tô thứ nhất đi được 20 phút, ô tô thứ hai cũng đi từ thành phố A đến thành phố B với vận tốc lớn hơn vận tốc ô tô thứ nhất là 6km/h (vận tốc không đổi trên cả quãng đường). Biết rằng cả hai ô tô đến thành phố B cùng một lúc.
1. Tính vận tốc của hai xe ô tô
2. Nếu trên đường đó có biển báo cho phép xe chạy với vận tốc tối đa là 50km/h thì hai xe ô tô trên, xe nào vi phạm về giới hạn tốc độ?

Hai đội công nhân cùng làm một công việc thì làm xong trong \(4\) giờ. Nếu mỗi đội làm một mình xong công việc đó thì đội thứ nhất cần ít thời gian hơn đội thứ hai là \(6\) giờ. Hỏi mỗi đội làm một mình xong công việc đó trong bao lâu.

Giải toán bằng cách lập phương trình hoặc hệ phương trình
Hưởng ứng phong trào Tết trồng cây, chi đoàn thanh niên dự định trồng 30 cây trong một thời gian nhất đinh. Do mỗi giờ chi đoàn trồng nhiều hơn dự định 5 cây nên đã hoàn thành công việc trước dự định 20 phút và trồng thêm được 10 cây nữa. Tính số cây mà chi đoàn dự định trồng trong mỗi giờ.

Để chở hết 60 tấn hàng, một đội xe dự định sử dụng một số xe cùng loại. Trước khi khởi hành, có 2 xe được điều động đi làm việc khác, vì vậy mỗi xe còn lại phải chở nhiều hơn dự định 1 tấn hàng. Hỏi lúc đầu đội dự định dùng bao nhiêu xe?

Giải Câu toán bằng cách lập phương trình hoặc hệ phương trình:
Hưởng ứng phong trào trồng cây xanh vì một môi trường xanh, sạch, đẹp. Một chi đoàn thanh niên dự định trồng 120 cây xanh. Nhưng khi thực hiện, chi đoàn đó đã tăng cường thêm 3 đoàn viên nữa nên mỗi đoàn viên đã trồng ít hơn 2 cây so với dự định. Hỏi lúc đầu chi đoàn thanh niên đó có bao nhiêu đoàn viên? (biết rằng số cây của mỗi đoàn viên trồng là như nhau)

Một đội xe dự định chở \(24\) tấn hàng. Thực tế khi chở đội được bổ sung thêm \(4\) xe nữa nên mỗi xe chở ít hơn dự định \(1\) tấn. Hỏi dự định ban đầu đội có bao nhiêu xe? (Biết khối lượng hàng chở trên mỗi xe như nhau).

Một lâm trường dự định trồng \(75\,{\rm{ha}}\) rừng trong một số tuần. Do mỗi tuần trồng vượt mức \(5\,{\rm{ha}}\) so với kế hoạch nên đã trồng được \(80\,{\rm{ha}}\) và hoàn thành sớm hơn \(1\) tuần. Hỏi mỗi tuần lâm trường dự định trồng bao nhiêu ha rừng?

Để chở hết 120 tấn hàng ủng hộ đồng bào vùng cao biên giới, một đội xe dự định dùng một số xe cùng loại. Lúc sắp khởi hành, họ được bổ sung thêm 5 xe cùng loại của đội, nhờ vậy, so với dự định ban đầu, mỗi xe phải chở ít hơn 2 tấn. Hỏi lúc đầu đội có bao nhiêu xe nếu khối lượng hàng mỗi xe phải chở bằng nhau?

Hai vòi nước cùng chảy vào một bể không có nước thì sau \[2\] giờ \[55\]phút sẽ đầy bể. Nếu để chảy một mình thì vòi thứ nhất chảy đầy bể nhanh hơn hơn vòi thứ hai là \[2\]giờ. Tính thời gian mỗi vòi chảy một mình đầy bể.

Để chở hết 120 tấn khoai lang ủng hộ bà con nông dân huyện Bình Sơn, tỉnh Quảng Ngãi vượt qua khó khăn do ảnh hưởng của đại dịch viêm đường hô hấp cấp nCovid – 19, một đội xe dự định dùng một số xe cùng loại. Lúc sắp khởi hành đội được bổ sung thêm 5 xe cùng loại, vì vậy so với dự định mỗi xe phải chở ít hơn 2 tấn. Hỏi lúc đầu đội có bao nhiêu xe?

Một đội xe theo kế hoạch chở hết \(120\) tấn hàng trong một số ngày quy định. Do mỗi ngày đội đó chở vượt mức \(5\) tấn nên đội đã hoàn thành kế hoạch sớm hơn thời gian quy định \(1\) ngày và chở thêm được \(5\) tấn. Hỏi theo kế hoạch đội xe chở hết số hàng đó trong bao nhiêu ngày

Giải Câu toán sau bằng cách lập phương trình hoặc hệ phương trình
Một đội xe cần vận chuyển \[160\] tấn gạo với khối lượng gạo mỗi xe chở bằng nhau. Khi sắp khởi hành thì đội được bổ sung thêm \[4\] xe nữa nên mỗi xe chở ít hơn dự định lúc đầu \[2\] tấn gạo (khối lượng gạo mỗi xe chở bằng nhau). Hỏi đội xe ban đầu có bao nhiêu chiếc?

Một đoàn xe vận tải dự định điều một số xe cùng loại để vận chuyển 40 tấn hàng. Lúc sắp khởi hành đoàn xe được giao thêm 14 tấn nữa. Do đó phải điều thêm 2 xe cùng loại trên và mỗi xe chở thêm 0,5 tấn. Tìm số lượng xe phải điều theo dự định, biết mỗi xe đều chở số lượng hàng như nhau và mỗi xe không chở quá 3 tấn hàng.

Một đoàn xe vận tải dự định điều một số xe cùng loại để vận chuyển 40 tấn hàng. Lúc sắp khởi hành đoàn xe được giao thêm 14 tấn nữa. Do đó phải điều thêm 2 xe cùng loại trên và mỗi xe phải chở thêm 0,5 tấn. Tìm số lượng xe phải điều theo dự định, biết mỗi xe đều chở số lượng hàng như nhau và mỗi xe chở không quá 3 tấn hàng.

Hai người thợ cùng làm chung một công việc sau \(3\) giờ \(36\) phút thì xong. Nếu mỗi người làm một mình thì người thứ nhất hoàn thành công việc chậm hơn người thứ hai là \(3\) giờ. Hỏi nếu làm một mình thì mỗi người phải làm trong bao nhiêu giờ để xong việc?

Hai vòi nước cùng chảy vào một bể cạn không có nước thì sau \(4\) giờ đầy bể. Nếu chảy riêng thì vòi thứ nhất sẽ chảy đầy bể nhanh hơn vòi thứ hai là \(6\) giờ. Hỏi nếu chảy riêng thì mỗi vòi mất bao lâu mới chảy đầy bể?

Giải Câu toán bằng cách lập phương trình hoặc hệ phương trình:
Một xí nghiệp theo kế hoạch phải lắp ráp \[800\] chiếc máy tính. Nếu một ngày lắp ráp thêm \[10\] máy tính thì không những hoàn thành sớm hơn \[1\] ngày so với kế hoạch mà còn lắp ráp thêm \[10\] máy tính. Tính số máy tính lắp ráp mỗi ngày theo kế hoạch?

Một phân xưởng theo kế hoạch phải dệt 3000 tấm vải để làm khẩu trang phục vụ các đơn vị tuyến đầu chống dịch. Trong 8 ngày đầu họ đã thực hiện được đúng kế hoạch, những ngày còn lại do nhu cầu cung cấp tăng lên họ đã dệt vượt mức mỗi ngày 10 tấm, nên đã hoàn thành kế hoạch trước 2 ngày. Hỏi theo kế hoạch mỗi ngày phân xưởng phải dệt bao nhiêu tấm vải?

Thực hiện kế hoạch “Mùa hè xanh” lớp \[9A\] được phân công trồng \[420\] cây. Lớp dự định chia đều số cây trồng cho mỗi học sinh trong lớp. Nhưng đến giờ trồng cây, có \[5\] bạn vắng, vì vậy mỗi bạn phải trồng thêm \[2\] cây nữa so với dự định. Hỏi số học sinh của lớp \[9A\]?

Người ta trộn 8g chất lỏng này với 6g chất lỏng khác có khối lượng riêng nhỏ hơn nó là 0,2g/\(c{m^3}\) để được hỗn hợp có khối lượng riêng 0,7g/\(c{m^3}\). Tìm khối lượng riêng của mỗi chất lỏng.

Người ta đổ thêm \(100\) g nước vào một dung dịch chứa \(20\)g muối thì nồng độ của dung dịch giảm đi \(10\% \). Hỏi trước khi đổ thêm nước thì dung dịch chứa bao nhiêu nước.

Người ta hòa lẫn \[7{\rm{ kg}}\] chất lỏng I với \[5{\rm{ kg}}\] chất lỏng II thì được một hỗn hợp có khối lượng riêng 600 \[{\rm{kg/}}{{\rm{m}}^{\rm{3}}}\]. Biết khối lượng riêng của chất lỏng I lớn hơn khối lượng riêng của chất lỏng II là 200 \[{\rm{kg/}}{{\rm{m}}^{\rm{3}}}\]. Tính khối lượng riêng của mỗi chất lỏng.

Để giúp xe lửa chuyển từ một đường ray từ hướng này sang một đường ray theo hướng khác, người ta làm xen giữa một đoạn đường ray hình vòng cung (hình 3.7). Biết chiều rộng của đường ray là \[AB = 1,1\]m, đoạn \[BC = 28,4\]m. Hãy tính bán kính \[OA = R\]của đoạn đường ray hình vòng cung.

Một khu đất trồng hoa lúc đầu hình chữ nhật có chiều dài 6,6 (m), người trồng hoa muốn mở rộng thêm về phía chiều rộng một hình vuông có cạnh \(x\) (m) để được khu đất có diện tích 34 (m2). Tìm chu vi của khu đất trồng hoa lúc sau?

Cho hình chữ nhật có chiều dài \(8\)cm, chiều rộng ngắn hơn đường chéo \(4\)cm. Tính diện tích hình chữ nhật.

Một hình chữ nhật có chiều rộng bằng một nửa chiều dài. Biết rằng nếu giảm mỗi chiều đi 2 m thì diện tích hình chữ nhật đã cho giảm đi một nửa. Tính chiều dài hình chữ nhật đã cho.

Một tam giác vuông có chu vi là 30 cm, độ dài hai cạnh góc vuông hơn kém nhau 7 cm. Tính độ dài các cạnh của tam giác vuông đó.