52 bài tập Hệ thức lượng trong tam giác có lời giải
52 câu hỏi
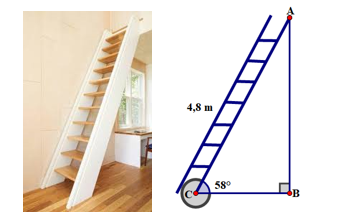
Một người thợ thiết kế một tầng lửng cho căn phòng của anh ấy. Anh ấy đã hoàn thành bản vẽ và tính toán được chiếc thang phải dài đặt nghiêng sao cho tạo với mặt sàn một góc . Hỏi độ cao của tầng lửng mà anh thiết kế là bao nhiêu mét? (Làm tròn kết quả đến chữ số thập phân thứ nhất).
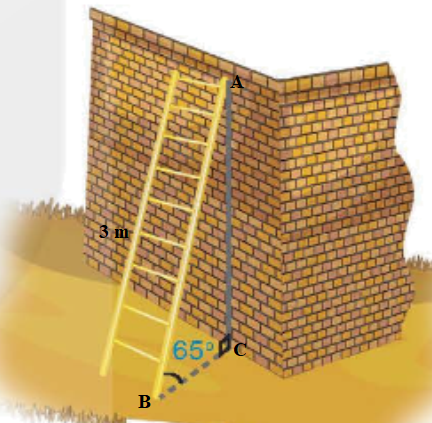
Bạn An có một chiếc thang dài 3 m. Cần đặt chân thang cách chân tường một khoảng cách bao nhiêu để nó tạo với mặt đất một góc "an toàn" là (tức là đảm bảo thang không bị đổ khi sử dụng). (kết quả làm tròn đến cm).
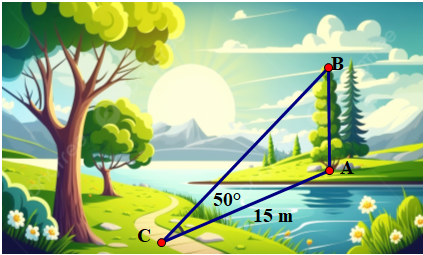
Một cái cây bên bờ một con sông có bề rộng \({\rm{AC}} = 15\;{\rm{m}}\), từ một điểm C đối diện với cây ngay bờ bên kia người ta nhìn thấy ngọn cây với góc nâng . Tính chiều cao AB của cây (kết quả làm tròn đến mét)
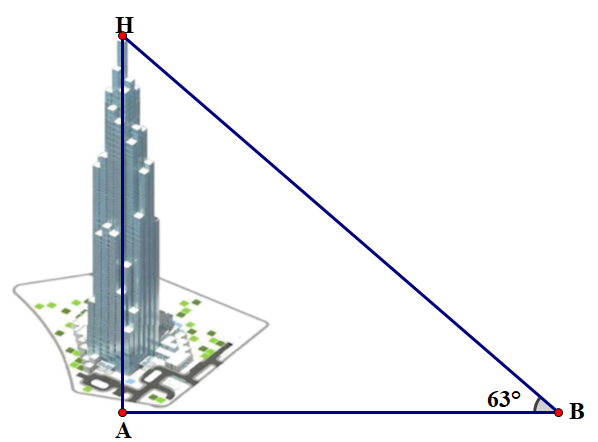
Tòa nhà Landmart 81 là một tòa nhà cao tầng ngay bên bờ sông Sài Gòn tại TP. Hồ Chí Minh. Tòa nhà này có 81 tầng, cao nhất Đông Nam Á (năm 2018). Ý tưởng thiết kế của The Landmark 81 được lấy cảm hứng từ những bó tre truyền thống tượng trưng cho sức mạnh và sự đoàn kết trong văn hóa Việt Nam. Tại một thời điểm tia sáng mặt trời tạo với mặt đất một góc là (góc B ) thì người ta đo được bóng của tòa nhà trên mặt đất dài khoảng 235 m (độ dài AB ). Hãy ước tính chiều cao của tòa nhà này (đoạn thẳng AH ) (làm tròn kết quả đến chữ số thập phân thứ nhất).
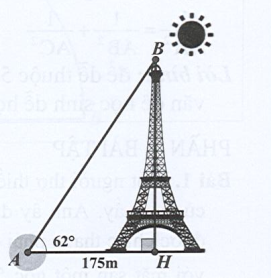
Tháp Eiffel là một công trình kiến trúc bằng thép nằm trên công viên Champ-de-Mars, cạnh sông Seinc, là biểu tượng của Thủ đô Paris nước Pháp. Công trình này do kỹ sư Gustave Eiffel và các đồng nghiệp của mình thiết kế, xây dựng từ năm 1887 đến năm 1889 nhân dịp Triển lãm thế giới năm 1889 và cũng là dịp kỷ niệm 100 năm Cách mạng Pháp. Hãy tính chiều cao của tháp Eiffel mà không cần lên đỉnh tháp khi biết góc tạo bởi tia nắng mặt trời với mặt đất là và bóng của tháp trên mặt đất là 175 m (làm tròn kết quả tới hàng đơn vị).
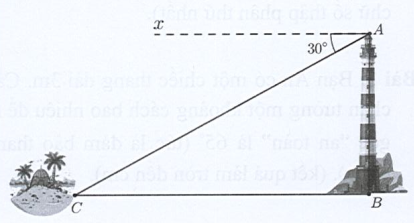
Từ đỉnh A của một ngọn đèn biển cao 70 m so với mặt nước biển, người ta nhìn thấy một hòn đảo C dưới góc so với đường nằm ngang chân đèn (xem hình vẽ, \(Ax{\rm{//}}BC\) ). Tính khoảng cách từ đảo C đến chân đèn B. (làm tròn đến hàng đơn vị).
Một cano chạy với tốc độ \(10\;{\rm{km}}/{\rm{h}}\) vượt qua một khúc sông nước chảy mạnh mất 6 phút. Biết rằng đường đi của ca nô tạo với bờ 1 góc . Tính chiều rộng BC của khúc sông? (làm tròn đến mét).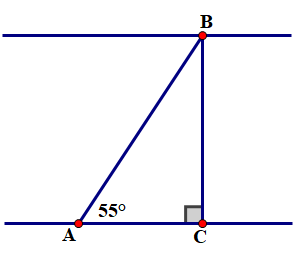
Một khúc sông rộng khoảng 250 m. Một chiếc thuyền muốn qua sông theo phương ngang nhưng bị dòng nước đẩy theo phương xiên, nên phải đi khoảng 320 m mới sang được bờ bên kia. Hỏi dòng nước đã đẩy thuyền lệch đi một góc bao nhiêu độ? (làm tròn đến độ).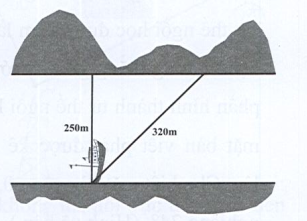
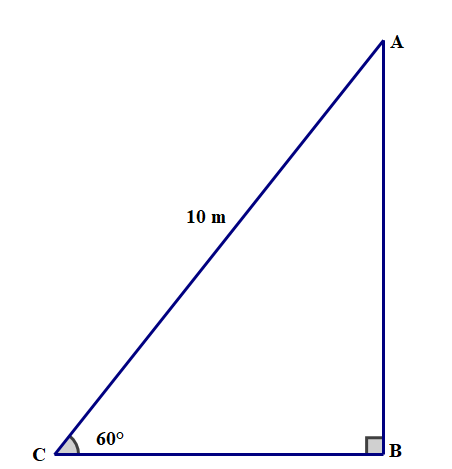
Ca nô kéo một người du khách mang dù bay lên không bằng một sợi dây dài 10 m tạo với mặt nước một góc . Hỏi khi đó, người du khách cách mặt nước biển bao nhiêu mét? (làm tròn đến chữ số thập phân thứ nhất)
Một chiếc máy bay xuất phát từ vị trí A bay lên với vận tốc \(500\;{\rm{km}}/{\rm{h}}\) theo đường thẳng tạo với phương ngang một góc nâng (xem hình). Hỏi sau 2 phút thì máy bay ở độ cao bao nhiêu? (làm tròn đến mét).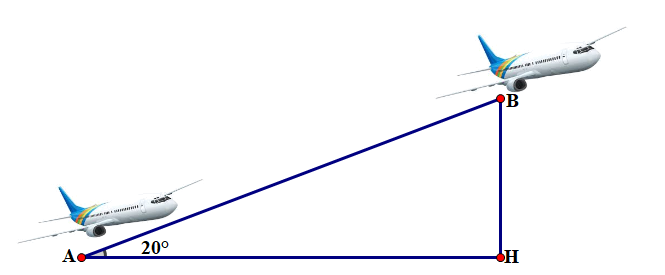
Một máy bay cất cánh với vận tốc trung bình là \(300\;{\rm{km}}/{\rm{h}}\), sau 6 phút máy bay cách mặt đất so với phương thẳng đứng là \(15.000 \cdot 000\;{\rm{m}}\). Hỏi đường bay lên của máy bay tạo với phương nằm ngang so với mặt đất một góc bằng bao nhiêu độ và khoảng cách từ điểm cất cánh đến chân của đường vuông góc hạ từ máy bay xuống mặt đất lúc này là bao nhiêu? (làm tròn đến hàng đơn vị).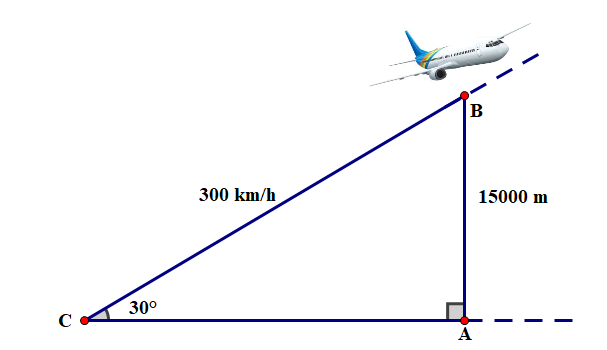
Một chuyến trượt cáp bắt đầu ở độ cao \(30m\)so với mặt đất. Chiều dài của cáp là \(100m\). Giả sử đường trượt cáp được cố định với mặt đất, hãy tính góc \(\widehat {{\rm{ABH}}}\) mà dây cáp tạo với mặt đất. (làm tròn câu trả lời của bạn chính xác đến phút)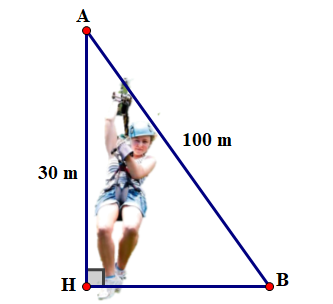
Tư thế ngồi học đúng
Tư thế ngồi học được xem là đúng khi khoảng cách từ mắt đến vở \(25 - 30\;{\rm{cm}}\), người ngồ học có lưng thẳng góc so với mặt đất. Bộ bàn học phù hợp với chiều cao học sinh sẽ gó phần hình thành tư thế ngồi học đúng. Một trong nhưng cách tạo ra bộ bàn ghế phù hợp là mặt bàn viết phải được kê nghiêng lên. Cho biết mặt bàn rộng \(0,6\;{\rm{m}}\), góc nghiêng . (Hình vẽ bên ) Hỏi mặt bàn viết được nâng lên \(({\rm{BC}})\) bao nhiêu mét? (làm tròn đến chữ số thập phân thứ hai)
Nóc mái nhà của một ngôi nhà là hình tam giác cân và được mô phỏng là một tam giác ABC cân tại A có đường cao AH. Người thọ đã đo được độ cao của đỉnh nóc nhà so với thanh ngang BC là \(1,2\;{\rm{m}}\) và chiều rộng ngôi nhà là \({\rm{BC}} = 8\;{\rm{m}}\). Tính độ dốc của mái nhà so với phương ngang là số đo góc ABC. (làm tròn đến phút).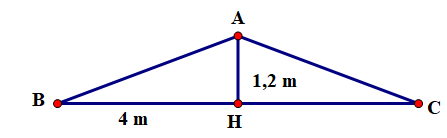
Một cái compa bằng nhôm của giáo viên dùng để vẽ đường tròn có hình dạng tam giác ABC cân tại A như hình vẽ và được mô phỏng lại ở hình bên. Biết chiều dài thanh compa là \({\rm{AB}} = 40\;{\rm{cm}}\). Để vẽ đường tròn có đường kính là 25 cm thì độ mở của hai thanh compa là \({\rm{BC}} = 25\;{\rm{cm}}\). Hỏi số đo góc ABC tạo bởi thanh compa là bao nhiêu độ? (kết quả số đo góc làm tròn đến phút)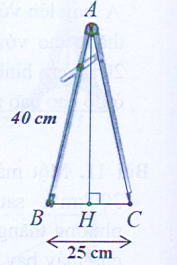
Một cây tre bị gãy ngang thân, ngọn tre vừa chạm đất và tạo với mặt đất một góc . Biết khoảng cách từ vị trí ngọn tre chạm đất tới gốc cây là \(4,5\;{\rm{m}}\). Tính chiều cao ban đầu của cây tre (làm tròn đến cm ).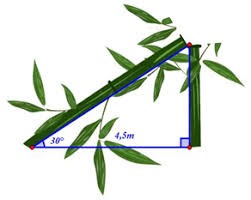
Chiều dài của một cái bập bênh là \(5,2\;{\rm{m}}\). Khi một đầu của bập bênh chạm đất thì cái bập bênh tạo với mặt đất góc như hình vẽ. Hỏi đầu còn lại cách mặt đất bao nhiêu mét? (Kết quả làm tròn đến hàng đơn vị).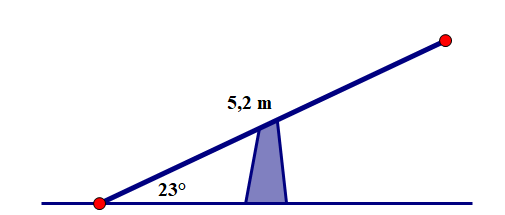
Để lắp đường điện cao thế từ vị trí A đến vị trí B cách nhau 2000 m, do phải tránh ngọn núi nên người ta nối đường dây từ vị trí A đến vị trí C, rồi nối từ vị trí C đến vị trí B. Góc tạo bởi hai đoạn dây CA và CB là và góc tạo bởi đoạn dây AC và đường AB là
a) Em hãy tính độ dài AC đường dây điện nối từ A đến C.
b) Em hãy tính chiều dài tăng thêm của đường dây diện vì không thể nối trực tiếp từ A đến B. (Kết quả làm tròn đến mét).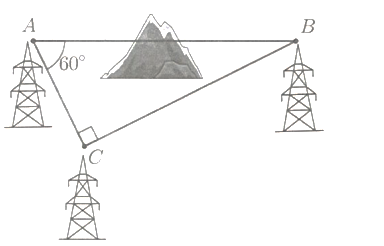
Một người đứng ở vị trí điểm C trên mặt đất cách tháp ăng ten một khoảng \({\rm{CD}} = 120\;{\rm{m}}\). Biết rằng người ấy nhìn thấy đỉnh tháp với so với đường nằm ngang, khoảng cách từ mắt đến mặt đất \({\rm{OC}} = 1,6\;{\rm{m}}\). Tính chiều cao AD của tháp (Làm tròn đến cm ).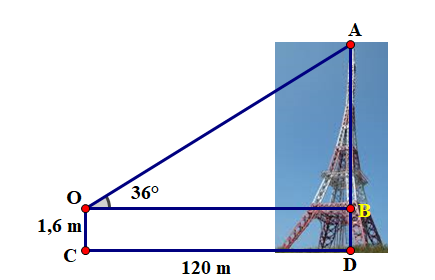
Một người cao 1,5 mét đứng cách nơi thả khinh khí cầu 250 mét nhìn thấy nó với góc nâng như hình vẽ. Tính độ cao của khinh khí cầu so với mặt đất? (kết quả làm tròn đến mét).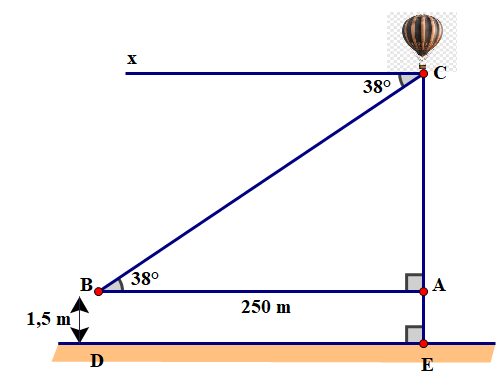
Ném còn là một trò chơi dân gian Việt Nam phổ biến trong các dịp lễ hội đầu năm của các dân tộc Tày, Thái, Mường,. chủ yếu ở vùng Tây Bắc. Ý nghĩa của trò chơi là cầu mong mùa màng tươi tốt, vạn vật sinh sôi nảy nở và cầu mong giao hoà âm dương, đất trời.
Trò chơi gồm một cây cọc thẳng lớn, thường làm bằng thân tre khá cao và có gắn một vòng tròn lớn trên ngọn. Cọc được đặt ở một sân bãi rộng rãi. Quả còn (trái còn) làm bằng vải nhiều màu chứa hạt bông, thóc hoặc cát, dây lược gắn với quả còn dài \(50 - 60\;{\rm{cm}}\). Người chơi đứng cách cây cọc một khoảng cách tương đối, sau đó cầm dây lược ném quả còn làm sao cho quả bay qua vòng tròn trên cây cọc là chiến thắng.
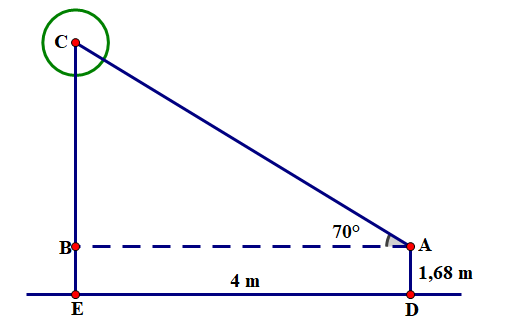
Tại lễ hội năm nay, một người chơi ném còn đứng cách chân cọc một khoảng 4 mét và góc nâng từ tầm mắt đến đỉnh ngọn cọc là 70 độ . Tính chiều cao của cọc (kết quả làm tròn đến mét). Biết rằng chiều cao từ mặt đất đến mắt người này là 1,68 mét.
Ở một cái thang dài 3 m người ta ghi: "Để đảm bảo an toàn khi dùng thang, phải đặt thang này tạo với mặt đất một góc có độ lớn từ 60 độ đến 75 độ ". Thực tế khi đặt thang đó dựa trên bờ tường tại A, ta rất khó đo góc tạo bởi thang và mặt đất (góc ABH ) nên thông thường ta sẽ đo khoảng cách BH giữa chân thang và chân tường. Theo em ta cần đặt chân chiếc thang đó cách bờ tường trong khoảng bao nhiêu mét để đảm bảo an toàn? Vì sao? (kết quả làm tròn một chữ số thập phân).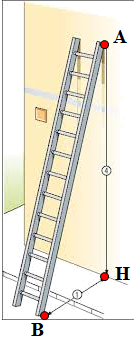
Từ vị trí C của một tòa nhà có chiều cao \({\rm{CD}} = 35\;{\rm{m}}\), người ta nhìn thấy đỉnh A của một tháp truyền hình với góc nâng (góc nâng là góc tạo bởi phương nằm ngang và tia đi qua đỉnh tháp) và từ vị trí C nhìn thấy chân của tháp với góc hạ (góc hạ là góc tạo bởi phương nằm ngang và tia đi qua chân tháp)
a) Tính khoảng cách BD từ tòa nhà đến chân tháp (kết quả làm tròn mét).
b) Tính chiều cao AB của tháp truyền hình (kết quả làm tròn mét)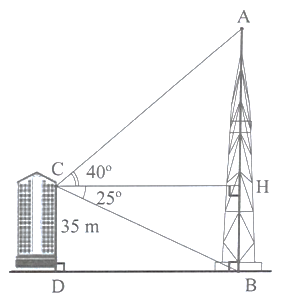
Bạn Nam đứng ở sân thượng nhà mình, cách cây xoài một khoảng \({\rm{AE}} = 20\;{\rm{m}}\) và quan sát thấy đỉnh cây B với góc và gốc cây A với góc so với phương ngang. Hãy tính chiều cao AB của cây xoài đó (kết quả làm tròn đến mét).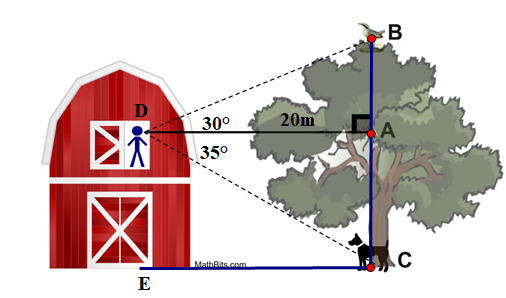
Một chiếc cầu trượt bao gồm phần cầu thang (để bước lên) và phần ống trượt (để trượt xuống) nối liền nhau như hình vẽ. Biết rằng khi xây dựng, phần ống trượt nghiêng với mặt đất một góc là , phần cầu thang (xem như đoạn thẳng AB ) nghiêng với mặt đất một góc , khoảng cách từ chân thang đến chân ống trượt là \(3,58\;{\rm{m}}\). Hãy tính độ cao AH của cầu trượt? (làm tròn đến chữ số thập phân thứ hai)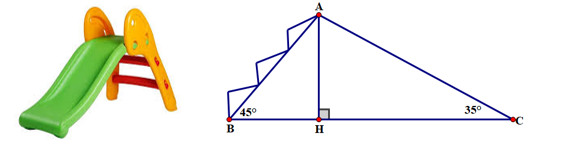
Điểm hạ cánh của một máy bay trực thăng ở giữa hai người quan sát A và B. Biết khoảng cách giữa hai người là 2500 m, góc nâng nhìn thấy máy bay tại vị trí A là và tại vị trí B là . Hãy tính độ cao của máy bay so với mặt đất? (kết quả làm tròn đến mét).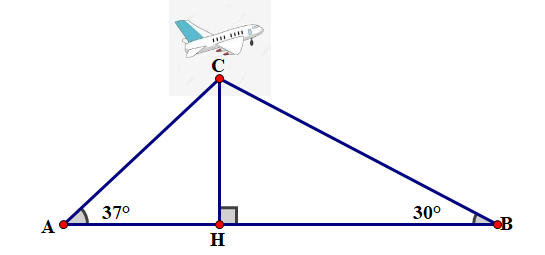
Trong bóng đá, đá phạt đền là một hình thức đá phạt trực tiếp giữa 1 cầu thủ và 1 thủ môn. Bóng sẽ được đặt ở vị trí nằm trên đường trung trực của khung thành và cách khung thành 11 m. Biết chiều dài khung thành là \(7,23\;{\rm{m}}\). Em hãy tính góc sút của cầu thủ \((\widehat {{\rm{BAC}}})\) (làm tròn đến độ).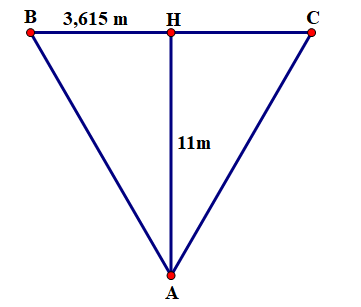
Để đo chiều cao của một ngọn hải đăng, người ta đặt giác kế tại 2 vị trí M và N sao cho các vị trí \({\rm{M}},{\rm{N}},{\rm{P}}\) cùng nằm trên một đường thẳng như hình vẽ. Kết quả thu được, vị trí M nhìn ngọn hải đăng dưới góc , vị trí N nhìn ngọn hải đăng dưới góc , khoảng cách giữa M và N là 24 m. Hỏi chiều cao \(DP\) của ngọn hải đăng là bao nhiêu mét? (làm tròn kết quả đến chữ số hàng đơn vị, học sinh không cần vẽ hình vào Câu làm).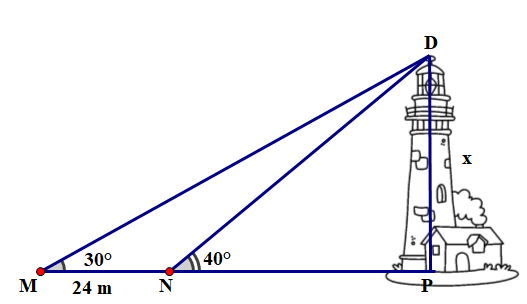
Một ngọn hải đăng cao 36 m nhìn về hướng Tây Nam có một chiếc thuyền D đang hướng về ngọn hải đăng, từ vị trí chiếc thuyền D nhìn lên ngọn hải đăng dưới một góc nâng là
a) Tính khoảng cách từ con thuyền D đến ngọn hải đăng (Tính AD ) (kết quả làm tròn 1 chữ số thập phân )
b) Cùng tại thời điểm đó, một chiếc thuyền C cũng đang hướng về ngọn hải đăng, từ vị trí chiếc thuyền C nhìn lên ngọn hải đăng dưới một góc nâng là . Hãy tính khoảng cách giữa 2 chiếc thuyền C và D. (điều kiện lý tưởng: vị trí 2 chiếc thuyền và vị trí ngọn hải đăng thẳng hàng) (kết quả làm tròn 1 chữ số thập phân).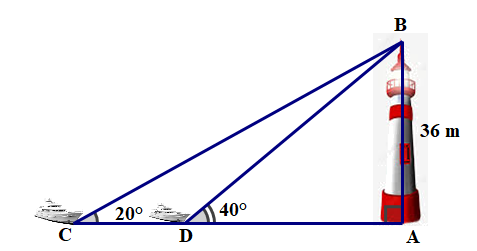
Một người đứng trên tòa nhà cao 180 m nhìn thấy hai chiếc xe ở vị trí C và D với góc hạ lần lượt là và . Tính khoảng cách CD của hai chiếc xe. (làm tròn đến chữ số thập phân thứ nhất)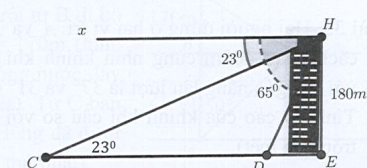
Một người đứng trên sân thượng tòa nhà cao tầng có khoảng cách từ mắt người ấy đến mặt đất là \({\rm{CD}} = 325\;{\rm{m}}\) nhìn thấy hai điểm A và B trên mặt đất với các góc hạ (góc nghiêng xuống so với phương nằm ngang) lần lượt là và (hình vẽ)
a) Tính độ dài AC (kết quả làm tròn mét).
b) Tính khoảng cách AB. Biết 3 điểm \({\rm{A}},{\rm{B}},{\rm{C}}\) thẳng hàng.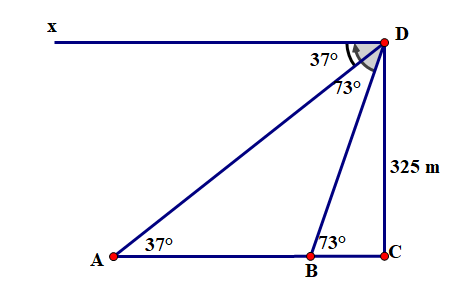
Từ máy bay trực thăng ở độ cao \(AB\) khoảng 700 m so với mặt đất, người ta nhìn thấy hai điểm \(M,N\) của hai cây cầu với góc hạ lần lượt là góc \(xBM\) bằng và góc \(xBN\) bằng . Em hãy tính chiều dài của cây cầu (kết quả làm tròn đến mét).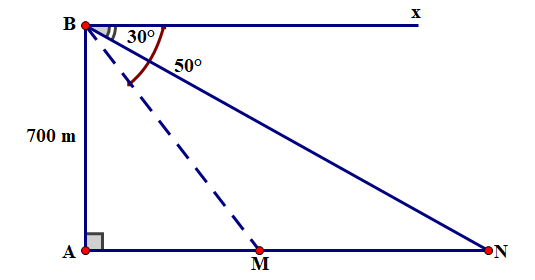
Một người đang ở vị trí \(B\) cách \(C\) là 400 m, quan sát hai lần một khinh khí cầu đang bay thẳng lên (như hình bên). Lần thứ nhất người đó nhìn thấy khinh khí cầu với góc nâng là , lần thứ hai người đó nhìn thấy khinh khí cầu với góc nâng là . Hỏi khinh khí cầu đã bay lên bao nhiêu mét giữa hai lần quan sát? (kết quả làm tròn đến hàng đơn vị).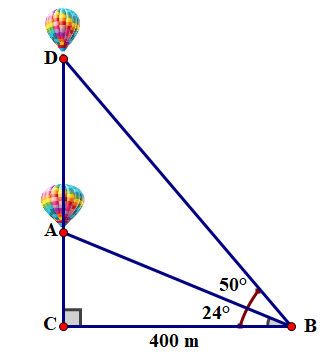
Tại một vị trí trên bờ bạn Nam có thề xác định được khoảng cách hai chiếc thuyền ở vị trí A và vị trí B như sau: Trước tiên, bạn chọn một vị trí trên bờ (điểm I) sao cho 3 điểm \({\rm{I}},{\rm{A}},{\rm{B}}\) thẳng hàng. Sau đó, bạn di chuyển theo hướng vuông góc với IA đến vị trí điểm K cách điểm I khoảng 380 m. Bạn dùng giác kế nhắm vị trí điểm A, điểm B thì đo được góc . Còn khi bạn nhắm vị trí điểm A, điểm I thì đo được . Hỏi khoảng cách hai chiếc thuyền là bao nhiêu? (kết quả làm tròn đến hàng đơn vị)
Hai người đứng ở hai vị trí \(A\) và \(B\) trên mặt đất cách nhau 400 m cùng nhìn khinh khí cầu (điểm \(C\) ) với các góc nâng lần lượt là và (như hình vẽ). Tính độ cao của khinh khí cầu so với mặt đất. (làm tròn đến mét).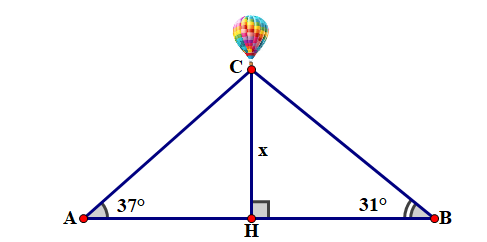
Tính chiều cao AH của máy bay so với mặt đất (làm tròn đến mét). Biết , góc ; góc 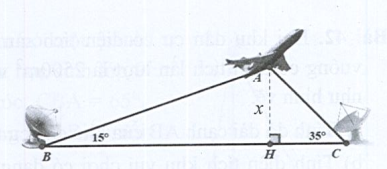
Bạn An đi từ nhà (điểm A ) đến trường (điểm C) phải leo lên và xuống như hình vẽ dưới. Cho biết chiều cao của con dốc là , Tính quãng đường của bạn An đi từ nhà đến trường? (làm tròn đến mét)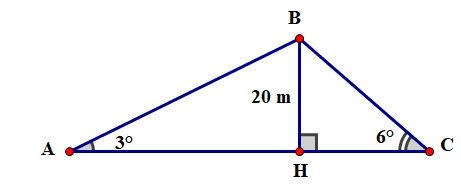
Hai người đứng bên bờ biển nhìn ra một hòn đảo, người thứ nhất nhìn ra đảo với một góc 350 so với bờ biển, người thứ hai nhìn ra đảo với một góc 430 độ so với bờ biển. Hai người đứng cách nhau \(1200m\). Hỏi hòn đảo cách bờ biển hai người đang đứng bao nhiêu? (làm tròn đến mét).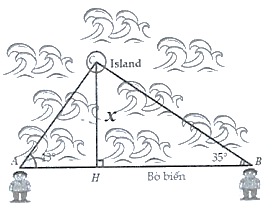
Câu 5: Điểm hạ cánh của một máy bay trực thăng ở giữa hai người quan sát A và B. Biết khoảng cách giữa hai người này là \(150m\), góc nâng tại vị trí A và B lần lượt là 410 và 520. Hãy tìm độ cao máy bay? (kết quả làm tròn đến mét).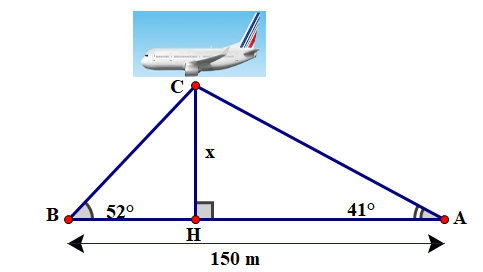
Một người đứng trên tháp quan sát của ngọn hải đăng có độ cao \(45m\) so với mực nước biển, người đó quan sát thấy hai con thuyền đang hướng về ngọn hải đăng. Người đó nhìn thấy con thuyền thứ nhất với góc hạ là 480, và nhìn thấy con thuyền thứ hai với góc hạ là 320. Hỏi khoảng cách của hai con thuyền lúc người quan sát nhìn thấy là bao nhiêu biết hai con thuyền và vị trí chân ngọn hải đăng là 3 điểm thẳng hàng? (kết quả làm tròn đến hàng đơn vị).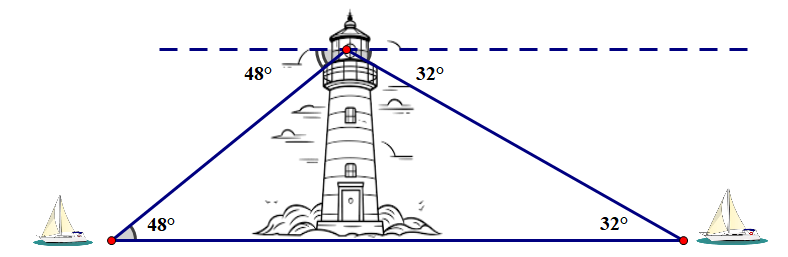
Mỗi ngày đi học, bạn Hùng phải đi đò (điểm \(A\) ) qua một khúc sông rộng 217 m đến điểm B (bờ bên kia), rồi từ B đi bộ đến trường tại điểm D với quãng đường \({\rm{BD}} = 170\;{\rm{m}}\) (hình bên). Thực tế, do nước chảy, nên chiếc đò bị dòng nước đẩy xiên một góc 500 đưa bạn tới điểm C (bờ bên kia). Từ C bạn Hùng đi bộ đến trường. Tính quãng đường mà Hùng đã đi từ A đến \(D\). (kết quả làm tròn đến chữ số thập phân thứ nhất).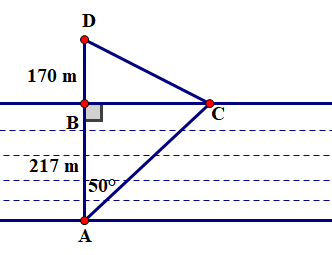
Hai khu dân cư có diện tích sàn là 2 hình vuông có diện tích lần lượt là \(2500\;{{\rm{m}}^2}\) và\(4900\;{{\rm{m}}^2}\)như hình vẽ.
a) Tính độ dài cạnh AB của khu dân cư thứ nhất.
b) Tính diện tích khu vui chơi có dạng hình tam giác ABC như trong hình biết số đo góc 1200 (làm tròn đến \(0,1\)).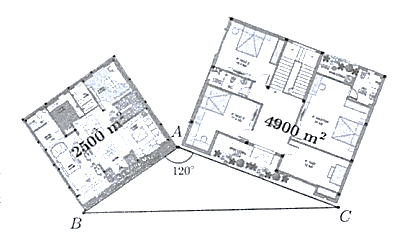
Để đo chiều cao của một bức tường Điệp dùng một quyển sách và ngắm sao cho hai cạnh bia của quyển sách hướng về vị trí cao nhất và vị trí thấp nhất của bức tường (xem hình bên). Biết rằng Điệp đứng cách tường \(1,5\;{\rm{m}}\) và vị trí mắt khi quan sát cách mặt đất là \(1,2\;{\rm{m}}\). Hỏi chiều cao của bức tường là bao nhiêu? (Kết quả làm tròn đến hàng đơn vị).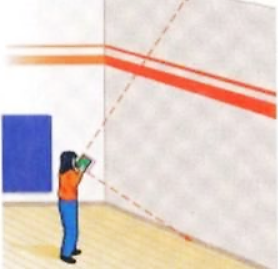
Bạn An đi xe đạp từ A đến địa điểm B phải leo lên một con dốc AC và xuống một con dốc CB (như hình vẽ A bên). Cho biết con dốc AC dài 440 m, góc
a) Tính chiều cao CH của con dốc theo đơn vị mét. (làm tròn đến hàng đơn vị).
b) Biết vận tốc trung bình lúc xuống dốc là \(18\;{\rm{km}}/{\rm{h}}\). Tính thời gian bạn An đi xe đạp xuống dốc từ C đến B (làm tròn đến giây).
Quan sát đỉnh \(T\) của một tháp từ các vị trí \(A\) và \(B\) ở một tòa nhà cao tầng. Biết khoảng cách AB là \(58m\); phương nhìn AT và BT tạo với phương ngang các góc lần lượt là 170 và 300; điểm B và D ở mặt đất. Tính khoảng cách từ đỉnh tháp đến mặt đất.(Tham khảo hình vẽ bên; làm tròn kết quả đến mét).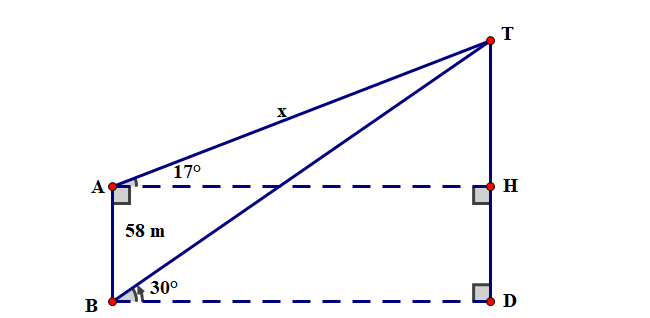
Trong trò chơi xích đu ở hình dưới, dây căng xích đu AK tạo với phương thẳng đứng một góc thì khoảng cách từ người chơi xích đu đi đến vị trí cân bằng (cột xích đu) là \({\rm{BK}} = 4\;{\rm{m}}\).
a) Tính chiều dài dây căng xích đu (AK).
b) Với kết quả ở câu a) em hãy tính khoảng cách từ ghế xích đu đến mặt đất (đoạn IH ) khi ghế ở vị trí cân bằng. Biết chiều cao cột xích đu \(({\rm{AH}})\) là \(6,6\;{\rm{m}}\).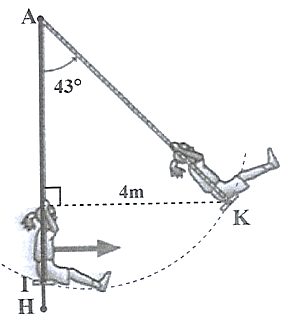
Trong sân trường THCS Đoàn Thị Điểm có một mảnh vườn hình tam giác ABC như hình vẽ. Một bạn học sinh lớp 9 dùng thước đo góc đo được góc , góc . Khoảng cách từ A đến B bạn đo được 15 gang tay. Biết mỗi gang tay của bạn dài \(22cm\).
a) Kẻ \({\rm{CH}} \bot {\rm{AB}}\) tại H. Chứng minh: \({\rm{CH}}.\cot A + {\rm{CH}} \cdot \cot B = {\rm{AB}}\) (học sinh vẽ hình khi làm Câu).
b) Hỏi mảnh vườn trên có diện tích bao nhiêu mét vuông? (kết quả làm tròn đến hàng đơn vị).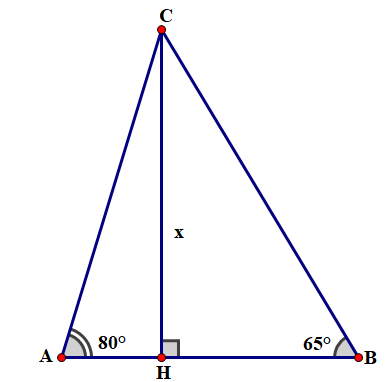
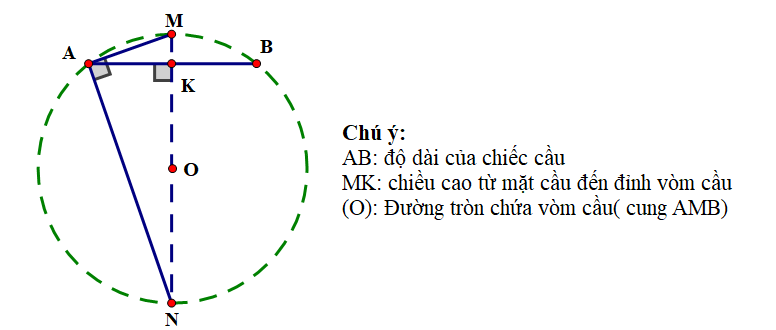
Một chiếc cầu dài 100 mét bắc qua một con sông được thiết kế kiểu mái vòm là một cung tròn như hình vẽ có chiều cao từ mặt cầu đến đỉnh vòm là 7 mét. Tính bán kính của đường tròn chứa cung tròn của vòm cầu (làm tròn đến chữ số thập phân thứ hai).
Một cơ cấu tay quay - con trượt được cho trong hình vẽ dưới.
Trong hình vẽ, điểm A là tâm của chốt piston và chỉ di chuyển theo chiều dọc. Điểm B là tâm của chốt khuỷu và chuyển động trên đường tròn \((O;r),{\rm{OB}}\) là tay quay, AB là thanh truyền. Điểm C là tâm quay tức thời của thanh truyền tại một thời điểm xác định. Biết vuông tại \({\rm{A}},{\rm{BH}} \bot {\rm{OA}}\) tại H, ba điểm \({\rm{O}},{\rm{B}},{\rm{C}}\) thẳng hàng, \({\rm{OB}} = 10\;{\rm{cm}},{\rm{AB}} = 14\;{\rm{cm}}\), \({\rm{AO}} = 20\;{\rm{cm}}\). Tính độ dài OH, số đo \(\widehat {{\rm{AOB}}}\) và độ dài BC (làm tròn kết quả số đo góc đến phút và số đo độ dài đến chữ số thập phân thứ hai).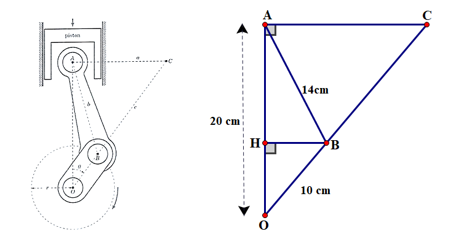
Hai xe máy khởi hành cùng lúc tại A và đi theo hai hướng tạo thành góc 600 như hình vẽ. Xe thứ nhất đi với vận tốc trung bình \(40\;{\rm{km}}/{\rm{h}}\), xe thứ hai đi với vận tốc trung bình \(50\;{\rm{km}}/{\rm{h}}\). Hỏi sau khi khởi hành 150 phút, hai xe cách nhau bao nhiêu km? (Kết quả làm tròn đến hàng đơn vị).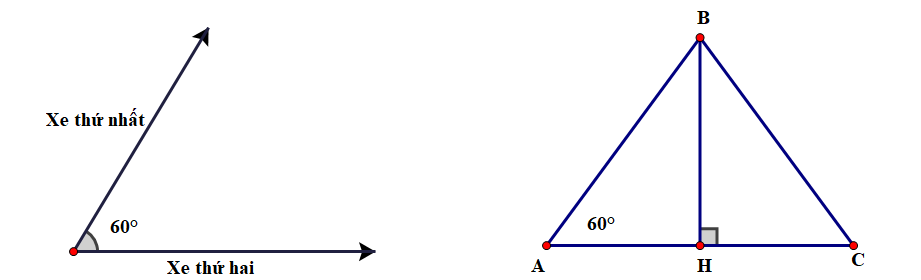
Một con đê được đắp chắn sóng theo hình dưới, biết , độ dốc của con đê phía biển dài \({\rm{AB}} = 8\;{\rm{m}}\). Hỏi độ dốc còn lại CD của con đê dài bao nhiêu mét? (Kết quả làm tròn đến chữ số thập phân thứ nhất).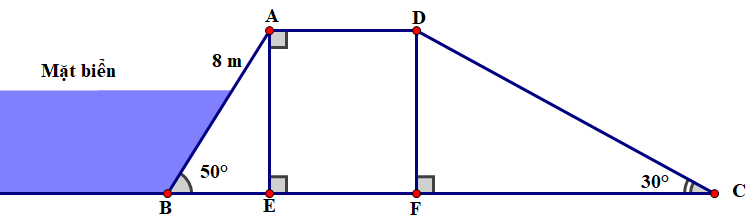
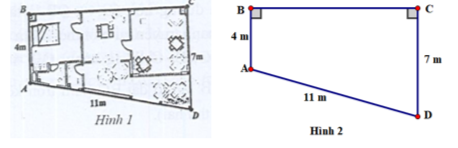
Hình 1 là bản vẽ thiết kế tầng trệt của một ngôi nhà (được mô phỏng lại ở hình 2). Biết \({\rm{AB}} \bot {\rm{BC}}\) tại \({\rm{B}};{\rm{CD}} \bot {\rm{BC}}\) tại C và \({\rm{AB}} = 4\;{\rm{m}},{\rm{CD}} = 7\;{\rm{m}},{\rm{AD}} = 11\;{\rm{m}}\). Em hãy tính số đo góc ADC hợp bởi hai bức tường AD và DC (Lưu ý: kết quả số đo góc làm tròn đến phút; học sinh vẽ hình số 2 vào giấy kiểm tra khi làm Câu 6 ).