45 bài tập Phương trình quy về phương trình bậc nhất 2 ẩn và hệ phương trình bậc nhất 2 ẩn có lời giải

Bác Hương bán hàng tạp hoá và có (đủ nhiều) các tờ tiền lẻ loại 2 nghìn đồng và 5 nghìn đồng. Bác cần trả lại cho một người mua hàng 25 nghìn đồng.a) Gọi \(x\) là số tờ tiền loại 2 nghìn đồng, \(y\) là số tờ tiền loại 5 nghìn đồng mà bác Hương cần trả lại cho khách \((x,y \in \mathbb{N})\). Hãy lập phương trình bậc nhất hai ẩn đối với \(x\) và \(y\).b) Hãy hỉ ra một nghiệm \((x;y)\) với \(x,y \in \mathbb{N}\) của phương trình lập ở câu a để tìm một phương án trả lại tiền thừa cho khách giúp bác Hương.

Một đội công nhân cần phải lắp đường ống dẫn nước trên một đoạn phố thẳng dài 65 m. Có hai loại ống dài 3 m và 5 m. Hãy chỉ ra ít nhất hai phương án lắp ống để không cần phải cưa ống ra (coi rằng các mối nối là không đáng kể).

Bác Ninh có hai khoản tiền thu được do bán bàn ăn và bàn làm việc cho công ty \({\rm{A}}\). Bàn ăn giá 500000 đồng/chiếc, bàn làm việc giá 700000 đồng/chiếc. Bác Ninh thu được tổng số tiền 11200000 đồng từ hai khoản tiền trên. Viết phương trình bậc nhất hai ẩn cho tổng số tiền bác Ninh thu được từ hai khoản tiền do bán bàn ăn và bàn làm việc cho công ty \({\rm{A}}\) và chỉ ra hai nghiệm của phương trình đó.

Hai trường \({\rm{A}}\) và \({\rm{B}}\) có tổng cộng 180 học sinh tham gia ngày hội STEM. Biết rằng \(15{\rm{\% }}\) học sinh trường \({\rm{A}}\) tham gia và \(10{\rm{\% }}\) học sinh trường \({\rm{B}}\) tham gia đạt giải. Tổng số học sinh hai trường \({\rm{A}}\) và \({\rm{B}}\) đạt giải là 22 học sinh. Gọi \(x\) và \(y\) lần lượt là số học sinh của trường \({\rm{A}}\) và trường \({\rm{B}}\) tham gia ngày hội đó.

a) Viết hệ hai phương trình bậc nhất hai ẩn \(x,y\) biểu thị mối quan hệ giữa các đại lượng.

b) Cặp số \(\left( {80;100} \right)\) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?

Ba bạn An, Bình, Chi cùng đi nhà sách. Cả ba bạn đã mua hết 279000 đồng. Ba bạn đã mua 3 quyển truyện với giá 45000 đồng/quyển và mua thêm bút bi, bút chì màu. Giá của bút bi và bút chì màu lần lượt là 3600 đồng/chiếc và 5000 đồng/chiếc. Gọi \(x\) và \(y\) lần lượt là số chiếc bút bi và bút chì màu mà ba bạn đã mua. Viết phương trình bậc nhất hai ẩn cho số tiền mà ba bạn đã dùng để mua bút bi, bút chì màu và chỉ ra một nghiệm của phương trình đó.

Cô Hà sử dụng dịch vụ điện thoại di động với giá cước gọi nội mạng và gọi ngoại mạng lần lượt là 1190 đồng/phút và 1390 đồng/phút. Trong tháng 10, cô Hà đã sử dụng 500 phút gọi (cả nội mạng và ngoại mạng) với tiền cước là 635000 đồng. Gọi \(x\) và \(y\) lần lượt là số phút gọi nội mạng và ngoại mạng trong tháng 10 của cô Hà.

a) Viết hệ hai phương trình bậc nhất hai ẩn \(x,y\) biểu thị mối quan hệ giữa các đại lượng.

b) Cặp số \((300\); 200) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?

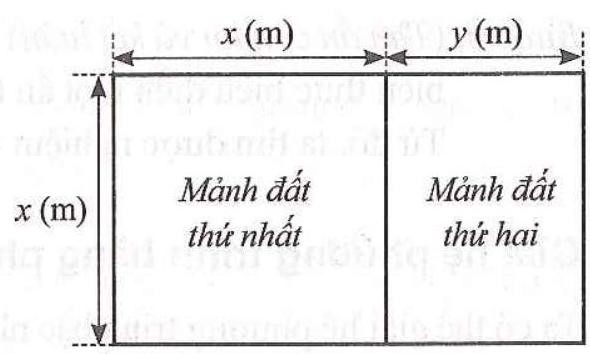
Người ta chia một khu đất có dạng hình chữ nhật thành hai mảnh đất: mảnh đất thứ nhất có dạng hình vuông với độ dài cạnh \(x\left( {{\rm{\;m}}} \right)\); mảnh đất thứ hai có đạng hình chữ nhật với chiều dài \(x\left( {{\rm{\;m}}} \right)\) và chiều rộng \(y\left( {{\rm{\;m}}} \right)(x > y > 0)\) được minh hoạ ở Hinh 3. Chu vi của mảnh đất thứ nhất lớn hơn chu vi của mảnh đất thứ hai là\(6,8{\rm{\;m}}\). Trên một cạnh là chiều dài của khu đất, người ta đã xây một tường rào với chi phí 1130000 đồng theo giá 50000 đồng/mét.

a) Viết hệ hai phương trình bậc nhất hai ẩn \(x,y\) biểu thị mối quan hệ giữa các đại lượng.

b) Cặp số \(\left( {13;9,6} \right)\) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?

Một ô tô đi từ địa điểm \(A\) đến địa điểm \(B\) với tốc độ \(x\left( {{\rm{\;km}}/{\rm{h}}} \right)\) thì đi hết \(y\) (giờ) với \(x > 10\) và \(y > 0,5\). Nếu tốc độ của ô tô giảm \(10{\rm{\;km}}/{\rm{h}}\) thì thời gian ô tô đi tăng 45 phút. Nếu tốc độ của ô tô tăng \(10{\rm{\;km}}/{\rm{h}}\) thì thời gian ô tô đi giảm 30 phút.

a) Viết hệ hai phương trình bậc nhất hai ẩn \(x,y\) biểu thị mối quan hệ giữa các đại lượng.

b) Cặp số \((50\); 3) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?

Một khu du lịch sinh thái bán vé vào cửa với giá 80 nghìn đồng mỗi vé, người cao tuổi được giảm giá 20 nghìn đồng mỗi vé. Vào một ngày cuối tuần, khu du lịch đã bán được 525 vé và thu về 35,8 triệu đồng.

Gọi \(x\) là số vé bán được ở mức giá 80 nghìn đồng và \(y\) là số vé bán được ở mức giá chiết khấu là 60 nghìn đồng.

a) Hãy viết một hệ hai phương trình liên quan đến các biến \(x\) và \(y\).

b) Giải hệ hai phương trình nhận được ở câu a để cho biết mỗi loại vé đã bán được bao nhiêu?

Trong kinh tế học, đường IS là một phương trình bậc nhất biểu diễn tất cả các kết hợp thu nhập \(Y\) và lãi suất \(r\) để duy trì trạng thái cân bằng của thị trường hàng hoá trong nền kinh tế. Đường LM là một phương trình bậc nhất biểu diễn tất cả các kết hợp giữa thu nhập \(Y\) và lãi suất \(r\) duy trì trạng thái cân bằng của thị trường tiền tệ trong nền kinh tế. Trong một nền kinh tế, giả sử mức thu nhập cân bằng \(Y\) (tính bằng triệu đô la) và lãi suất cân bằng \(r\) thoả mãn hệ phương trình\(\left\{ {\begin{array}{*{20}{l}}{0,06Y - 5000r = 240}\\{0,06Y + 6000r = 900.}\end{array}} \right.\). Tìm mức thu nhập và lãi suất cân bằng.

Phương trình cung và phương trình cầu của một loại thiết bị kĩ thuật số cá nhân mới là:

Phương trình cầu: \(p = 150 - 0,00001x\); Phương trình cung: \(p = 60 + 0,00002x\); trong đó \(p\) là giá mỗi đơn vị sản phẩm (tính bằng đô la) và \(x\) là số lượng đơn vị sản phẩm. Tìm điểm cân bằng của thị trường này, tức là điểm \((p;x)\) thoả mãn cả hai phương trình cung và cầu.

Thầy Nam dạy Toán đang thiết kế một bài kiểm tra trắc nghiệm gồm hai loại câu hỏi, câu hỏi đúng/sai và câu hỏi nhiều lựa chọn. Bài kiểm tra sẽ được tính trên thang điểm 100, trong đó mỗi câu hỏi đúng/sai có giá trị 2 điểm và mỗi câu hỏi nhiều lựa chọn có giá trị 4 điểm. Thầy Nam muốn số câu hỏi nhiều lựa chọn gấp đôi số câu hỏi đúng/sai.

a) Gọi số câu hỏi đúng/sai là \(x\), số câu hỏi nhiều lựa chọn là \(y\left( {x,y \in {\mathbb{N}^*}} \right)\). Viết hệ hai phương trình biểu thị số lượng của từng loại câu hỏi.

b) Giải hệ phương trình trong câu a để biết số lượng câu hỏi mỗi loại trong bài kiểm tra là bao nhiêu.

Một công ty sản xuất đĩa CD có giá sản xuất là 15 nghìn đồng cho một đĩa CD. Công ty có chi phí cố định hằng tháng là 120 triệu đồng (là chi phí mà công ty phải thanh toán định kì hằng tháng, dù không sản xuất gì). Nếu mỗi đĩa CD có thể bán với giá 30 nghìn đồng thì mỗi tháng phải bán được bao nhiêu đĩa CD để hoà vốn?

Đĩa CD

Để trả lời câu hỏi này, hãy lần lượt thực hiện các yêu cầu sau:

a) Xác định công thức tính tổng chi phí \(C\) khi công ty sản xuất \(x\) chiếc đĩa CD trong tháng.

b) Xác định công thức tính doanh thu \(R\) khi công ty bán được \(x\) chiếc đĩa CD.

Từ đó, sử dụng hai công thức đã lập để xác định điểm hoà vốn trong sản xuất, tức là mức sản xuất và bán được để tổng chi phí sản xuất bằng với doanh thu.

Vào năm 2005, có tổng cộng 55 lần phóng vệ tinh thương mại và phi thương mại trên toàn thế giới. Ngoài ra, số lần phóng vệ tinh phi thương mại nhiều hơn 1 lần so với hai lần số lần phóng vệ tinh thương mại. Tính số lần phóng vệ tinh thương mại và phi thương mại trong năm 2005.

Một ca nô đi ngược dòng sông một quãng đường 6 km thì hết \(\frac{3}{2}\) giờ. Mặt khác, ca nô đó chỉ mất 45 phút để đi xuôi dòng sông một quãng đường tương tự. Tính vận tốc thực của ca nô và vận tốc của dòng nước.

Để pha chế 1000 lít cồn nồng độ \(16\% \), người ta trộn lẫn dung dịch cồn nồng độ \(10\% \) và dung dịch cồn nồng độ \(70\% \). Tính số lít mỗi dung dịch cồn nồng độ \(10\% \) và nồng độ \(70\% \) cần dùng.

Chị Hương tập thể dục vào mỗi buổi sáng trong vòng 40 phút. Chị ấy kết hợp giữa thể dục nhịp điệu giúp đốt cháy khoảng 11 calo mỗi phút và giãn cơ giúp đốt cháy khoảng 4 calo mỗi phút. Mục tiêu của chị là đốt cháy 335 calo trong mỗi buổi tập sáng của mình.

a) Viết hệ phương trình biểu thị thời gian chị dành cho mỗi hoạt động tập.

b) Từ hệ phương trình lập được ở câu a, tính thời gian chị nên dành cho mỗi hoạt động tập để đạt được mục tiêu của mình.

Điểm mà tại đó chi phí sản xuất của công ty bằng doanh thu của nó được c gọi là điểm hoà vốn. Dưới đây, \(C\) thể hiện chi phí sản xuất (tính bằng đô la) của \(x\) đơn vị sản phẩm và \(R\) thể hiện doanh thu (tính bằng đô la) từ việc bán \(x\) đơn vị sản phẩm. Tìm số lượng sản phẩm cần sản xuất và bán để hoà vốn, nghĩa là tìm giá trị của

\(x\) để \(C = R\) với\(\left\{ {\begin{array}{*{20}{l}}{C = 15x + 12000}\\{R = 18x - 6000.}\end{array}} \right.\) Tính doanh thu của công ty khi đó.

Một buổi biểu diễn ca nhạc bán được 1500 vé. Mỗi vé loại I có giá 250 nghìn đồng và mỗi vé loại II có giá 150 nghìn đồng. Tổng số tiền bán vé thu được là 285 triệu đồng. Hỏi mỗi loại vé đã bán được bao nhiêu vé?

Một khẩu phần súp cà chua chứa 100 calo và 18 gam carbohydrate. Một lát bánh mì nguyên hạt chứa 70 calo và 13 gam carbohydrate. Cần bao nhiêu khẩu phần mỗi loại để có được 230 calo và 42 gam carbohydrate?

Một loại xe ô tô có mức tiêu hao nhiên liệu là 8,1 lít/100 km khi lái xe trong thành phố và 4,8 lít/ 100 km khi lái xe trên đường cao tốc. Vào một ngày Chủ nhật, chiếc xe đi tổng quãng đường trong thành phố và trên đường cao tốc là 165 km và tiêu thụ hết 8,415 lít xăng. Tính độ dài quãng đườnng xe ô tô đi trong thành phố và trên đường cao tốc vào ngày Chủ nhật đó.

Một mảnh vườn hình chữ nhật có chu vi\[34{\rm{ }}m\]. Nếu tăng chiều dài thêm \[3{\rm{ }}m\]và tăng chiều rộng thêm \[2{\rm{ }}m\]thì diện tích tăng thêm \(45\;{{\rm{m}}^2}\). Tính chiều dài và chiều rộng của mảnh vườn.

Trong cuộc thi Olympic Toán học. Nhóm học sinh đã trả lời 20 câu hỏi và kết quả mà nhóm đạt được là 28 điểm. Tính số câu trả lời đúng và sai của nhóm. Biết rằng mỗi câu trả lời đúng được 2 điểm, còn trả lời sai thì bị trừ 1 điểm.

Một người đi siêu thị điện máy mua một cái quạt điện và một cái bàn ủi điện, biết tổng số tiền theo giá niêm yết của hai sản phẩm là 900000 đồng. Siêu thị đang có chương trình giảm giá, quạt điện được giảm giá \(15\% \), bàn ủi điện được giảm giá \(10\% \) nên thực tế người đó chỉ phải thanh toán tổng số tiền cho hai sản phẩm là 780000 đồng. Tính được giá niêm yết của cái quạt điện và cái bàn ủi điện?

Trong tháng 9, hai tổ sản xuất được 1100 chi tiết máy. Sang tháng 10, tổ Một sản xuất vượt mức \(15\% \), tổ Hai sản xuất vượt mức \(20\% \) so với tháng 9, do đó tháng 10 hai tổ sản xuất được 1295 chi tiết máy. Hỏi trong tháng 9 mỗi tổ sản xuất được bao nhiêu chi tiết máy?

Một ô tô di chuyển trên quãng đường AB với tốc độ \(60\;{\rm{km}}/{\rm{h}}\), rồi tiếp tục di chuyển trên quãng đường BC với tốc độ \(55\;{\rm{km}}/{\rm{h}}\). Biết tổng chiều dài quãng đường AB và BC là 200 km và thời gian ô tô đi hết quãng đường AB ít hơn thời gian đi hết quãng đường BC là 30 phút. Tính thời gian ô tô di chuyển hết mỗi quãng đường.

Một mảnh vườn hình chữ nhật có chu vi 360 m. Biết chiều dài của mảnh vườn bằng \(\frac{5}{4}\) lần chiều rộng. Tính chiều dài và chiều rộng của mảnh vườn.

Để tổ chức tham quan khu di tích Bến Nhà Rồng (Thành phố Hồ Chí Minh) cho 195 người gồm học sinh khối lớp 9 và giáo viên phụ trách, nhà trường đã thuê 5 chiếc xe gồm hai loại: loại 45 chỗ và loại 30 chỗ. Hỏi nhà trường cần thuê bao nhiêu xe mỗi loại để chở hết số người đó? (Biết rằng trường mong muốn các xe không còn chỗ trống.)

Một vật là hợp kim của đồng và kẽm có khối lượng 124 g và thể tích \(15\;{\rm{c}}{{\rm{m}}^3}\). Tính xem trong đó có bao nhiêu gam đồng và bao nhiêu gam kẽm, biết rằng cứ 89 g đồng thì có thể tích là \(10\;{\rm{c}}{{\rm{m}}^3}\)và 7g kẽm có thể tích là \(1\;{\rm{c}}{{\rm{m}}^3}\).

Một người mua 36 bông hoa hồng và hoa cẩm chướng hết tất cả 174000 đồng. Giá mỗi bông hoa hồng là 5500 đồng, giá mỗi bông hoa cẩm chướng là 4000 đồng. Hỏi người đó đã mua bao nhiêu bông hoa mỗi loại?

Một xe tải dự định di chuyển từ A đến B với tốc độ không đổi trong một thời gian nhất định. Nếu tốc độ của xe giảm \(10\;{\rm{km}}/{\rm{h}}\) thì đến \(B\) chậm hơn dự định 45 phút. Nếu tốc độ của xe nhanh hơn tốc độ dự định \(10\;{\rm{km}}/{\rm{h}}\) thì sẽ đến B sớm hơn dự định 30 phút. Tính tốc độ và thời gian dự định của xe tải đó.

Một gia đình có bốn người lớn và ba trẻ em mua vé xem xiếc hết 370000 đồng. Một gia đình khác có hai người lớn và hai trẻ em cũng mua vé xem xiếc tại rạp đó hết 200000 đồng. Hỏi giá bán của mỗi loại vé cho người lớn và trẻ em là bao nhiêu? Biết rằng rạp đó bán hai hạng vé: người lớn và trẻ em, mỗi người vào xem phải mua một vé đúng hạng.

Một trường tuyển được 85 học sinh vào hai lớp năng khiếu bóng rổ và bóng chuyền. Nếu chuyển 25 học sinh từ lớp bóng rổ sang lớp bóng chuyền thì số học sinh của lớp bóng chuyền bằng \(\frac{{12}}{5}\) số học sinh của lớp bóng rổ. Hãy tính xem mỗi lớp có bao nhiêu học sinh.

Hai khối hợp kim có tỉ lệ đồng và kẽm khác nhau: Khối thứ nhất có tỉ lệ đồng và kẽm là \[8:2\]và khối thứ hai có tỉ lệ đồng và kẽm là\[3:7\], được đưa vào lò để luyện ra khối hợp kim có khối lượng 250 kg và có tỉ lệ đồng và kẽm là \[5:5\]. Tính khối lượng mỗi khối hợp kim. (Biết rằng, khối lượng hao hụt và khối lượng các tạp chất không đáng kể).

Để mở rộng kinh doanh, một cửa hàng đã vay 600 triệu đồng kì hạn 12 tháng từ hai ngân hàng \({\rm{A}}\) và \({\rm{B}}\) với lãi suất lần lượt là \(8{\rm{\% }}/\) năm và \(9{\rm{\% }}/\) năm. Tổng số tiền lãi một năm phải trả cho cả hai ngân hàng đó của cửa hàng là 51,5 triệu đồng. Tính số tiền mà cửa hàng đã vay từ mỗi ngân hàng.

Một nhà máy sản xuất hai loại xi măng: loại \({\rm{I}}\) và loại II. Cứ sản xuất mỗi tấn xi măng loại I thì nhà máy thải ra \(0,5{\rm{\;kgC}}{{\rm{O}}_2}\) (carbon dioxide) và \(0,3{\rm{\;kgS}}{{\rm{O}}_3}\) (sulfur trioxide), sản xuất mỗi tấn xi măng loại II thì nhà máy thải ra \(0,8{\rm{\;kgC}}{{\rm{O}}_2}\) và \(0,45{\rm{\;kgS}}{{\rm{O}}_3}\). Trung bình mỗi ngày, nhà máy nhận được thông số lượng khí thải \({\rm{C}}{{\rm{O}}_2}\) và \({\rm{S}}{{\rm{O}}_3}\) lần lượt là \(1700{\rm{\;kg}}\) và \(975{\rm{\;kg}}\). Tính khối lượng xi măng loại \({\rm{I}}\) và loại II trung bình mỗi ngày nhà máy sản xuất được.

Bác Lan có 500 triệu đồng để đầu tư vào hai khoản: trái phiếu và gửi tiết kiệm ngân hàng với kì hạn 12 tháng. Lãi suất của trái phiếu và gửi tiết kiệm ngân hàng lần lượt là \(7{\rm{\% }}/\) năm và \(6{\rm{\% }}/\) năm. Tính số tiền mà bác Lan đầu tư vào mỗi khoản để mỗi năm nhận được tiền lãi là 32 triệu đồng từ hai khoản đầu tư đó.

Một ô tô dự định đi từ địa điểm \(A\) đến địa điểm \(B\) trong một khoảng thời gian nhất định. Nếu ô tô đi với tốc độ \(40{\rm{\;km}}/{\rm{h}}\) thì ô tô đến địa điểm \(B\) chậm hơn 90 phút so với dự định. Nếu ô tô đi với tốc độ \(60{\rm{\;km}}/{\rm{h}}\) thì ô tô đến địa điểm \(B\) nhanh hơn 30 phút so với dự định. Tính quãng đường \(AB\) và thời gian ô tô dự định đi.

Một cửa sổ có dạng hình chữ nhật được xây trên bức tường có dạng hình thang vuông với các kích thước như Hinh 4. Tìm \(x,y\), biết rằng diện tích của bức tường không tính phần làm cửa sổ là \(69{\rm{\;}}{{\rm{m}}^2}\) và \(2x = y - 3\).

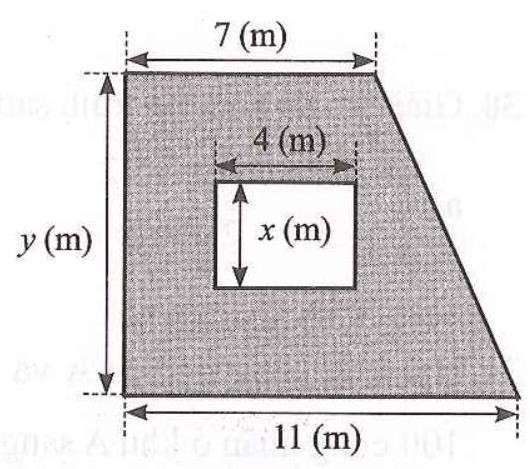
Hinh 4

Hai đội công nhân cùng đào đất để đắp đê ngăn triều cường. Nếu hai đội cùng làm thì 2 ngày hoàn thành công việc. Nếu đội thứ nhất làm trong 4 ngày rồi nghỉ, đội thứ hai làm tiếp trong 1 ngày nữa thì hoàn thành công việc. Tính thời gian mỗi đội làm riêng để hoàn thành công việc.

Chi phí để anh Hưng và ban nhạc của anh thu âm đĩa CD đầu tiên là 30 triệu đồng và mỗi đĩa CD sẽ có giá 8 nghìn đồng để sản xuất. Nếu ban nhạc bán đĩa CD của mình với giá 20 nghìn đồng mỗi đĩa thì phải bán bao nhiêu đĩa để hoà vốn (tức là doanh thu bằng với chi phí thu âm và sản xuất)?

Một cửa hàng sách có hai khu sách mới và sách cũ, mỗi khu được bán đồng giá. Mai chi 112500 đồng để mua 3 cuốn sách mới và 4 cuốn sách cũ, còn Linh chi 157500 đồng để mua 10 cuốn sách cũ và 3 cuốn sách mới. Tính giá mỗi cuốn sách mới và giá mỗi cuốn sách cũ.

Chuyến bay thẳng của hãng hàng không Delta Air Lines (một hãng hàng không của Mỹ) trên chặng Atlanta - Paris dài 4000 dặm, mất khoảng 8 giờ để đi từ Atlanta đến Paris (đi về phía đông) và mất 10 giờ để đi từ Paris đến Atlanta (đỉ về phía tây). Mặc dù máy bay có vận tốc riêng (tức là vận tốc so với không khí) không đ̛ổi, nhưng có gió ngược khi di chuyển về phía tây và gió thuận khi di chuyển về phía đông nên vận tốc của máy bay so với mặt đất là khác nhau tuỳ vào hướng di chuyển của máy bay. Tính vận tốc riêng của máy bay và vận tốc gió.

Hùng dự định chạy 4 km trong tuần tập luyện đầu tiên và tăng quãng đường chạy thêm 1 km mỗi tuần. Trong khi đó, Huy lại dự định sẽ bắt đầu chạy 1 km trong tuần đầu tiên và sau đó tăng thêm 2 km mỗi tuần. Hỏi ở tuần thứ bao nhiêu thì hai người có tổng quãng đường chạy là bằng nhau và quãng đường đó là bao nhiêu kilômét?