123 bài tập Nón trụ cầu và hình khối có lời giải

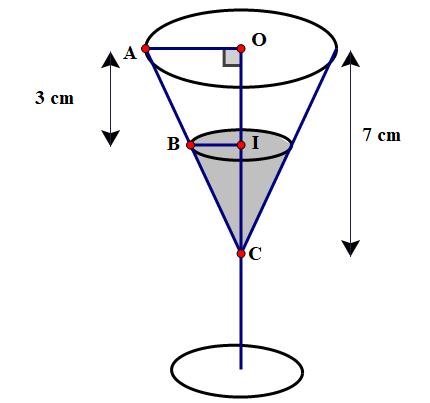
Vừa qua trên mạng xã hội, nhiều người dùng truyền tai nhau hình ảnh về một hiện tượng tự nhiên vô cùng kỳ lạ, xuất hiện vào sáng ngày 24/11/2022. Được biết, bức ảnh này được chụp lại núi Bà Đen, một địa điểm du lịch vô cùng nổi tiếng của Tây Ninh.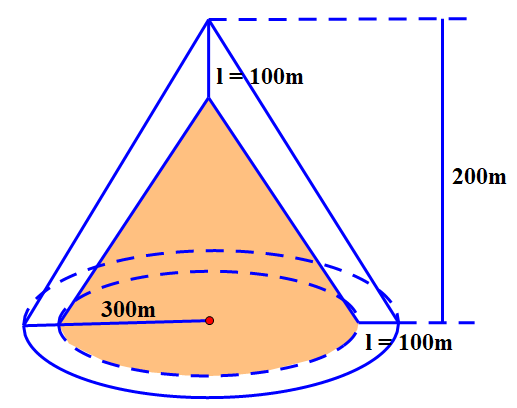 Trong hình ảnh, đỉnh núi được bao phủ bởi một lớp mây trắng xóa. Không chỉ có vậy, những đám mây còn tạo thành một lớp “vỏ” có phần kỳ bí. Nhiều người gọi đây là hiện tượng “mây vờn”, có người nhận xét trông đám mây như một chiếc nón. Ước tính chiều cao của nón là 200 m, bán kính đáy của nón là 300 m, độ dày đám mây là \(l = 100\;m\). Tính thể tích đám mây?
Biết thể tích hình nón là \(V = \frac{1}{3}\pi {R^2}\;h\) (trong đó \(R\) là bán kính đường tròn đáy; \(h\) là chiều cao hình nón, lấy \(\pi \approx 3,14\), các kết quả làm tròn chữ số thập phân thứ nhất).

Nón lá Câu thơ là một đặc trưng của xứ Huế. Nón thường được đan bằng các loại lá khác nhau như lá cọ, lá buông, rợ, tre, lá cối, lá hồ, lá du quy diệp chuyên làm nón,. Để làm ra một chiếc nón lá người thợ thủ công lấy từng chiếc lá, làm cho phẳng rồi lấy kéo cắt chéo đầu trên, rối lấy kim xâu chúng lại với nhau một lượt, sau đó xếp đều trên khuôn nón. Lá nón mỏng và cũng dễ hư khi gặp trời mưa nhiều nên các thợ thủ công đã tận dụng bẹ tre khô để làm lớp giữa hai lớp lá nón làm cho nón vừa cứng lại vừa bền. Đường kính của vòng tròn lớn nhất của chiếc nón khoảng 40 cm; chiều cao của chiếc nón là khoảng 19 cm. Hỏi cần bao nhiêu chiếc lá đã làm phẳng đề làm thành 1 chiếc nón lá, biết rằng diện tích 1 chiếc lá làm phẳng là \(72\;c{m^2}\), diện tích xung quanh của hình nón là \({S_{xq}} = \pi rl(\pi = 3,14\); làm tròn đến hàng đơn vị)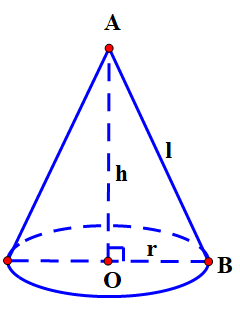

Một hình nón có bán kính đáy bằng \(5cm\) và diện tích xung quanh là \(65\pi \)\(c{m^2}\). Tính thể tích của hình nón đó.

Nón Huế là một hình nón có đường kính đáy bằng \[40cm\], độ dài đường sinh là \[30cm\]. Người ta lát mặt xung quanh hình nón bằng ba lớp lá khô. Tính diện tích lá cần dùng đề tạo nên một chiếc nón Huế như vậy (làm tròn \[c{m^2}\])

Chiến nón do làng Chuông (Thanh Oai – Hà Nội) sản xuất là hình nón có đường sinh bằng \(30{\rm{cm}}\), đường kính bằng \(40{\rm{cm}}\). Người ta dùng hai lớp lá để phủ lên bề mặt xung quanh của nón.

Nhân ngày 8/3, Hoa định mua một chiếc nón lá để tặng cô Anna - cô giáo dạy tiếng Anh. Chiếc nón có dạng hình nón với đường kính của đáy là 40cm, chiều cao của nón là 20cm. Hãy tính được diện tích lá cần dùng để phủ kín một lớp lên bề mặt của chiếc nón?

Nhà hát Cao Văn Lầu, Trung tâm triển lãm văn hóa nghệ thuật tỉnh Bạc Liêu có hình dáng \(3\) chiếc nón lá lớn nhất Việt Nam, mái nhà hình nón làm bằng vật liệu composite và được đặt hướng vào nhau. Em hãy tính thể tích của một mái nhà hình nón biết đường kính là \(45m\) và chiều cao là \(24m\) (lấy \(\pi \approx 3,14\), kết quả làm tròn đến hàng đơn vị, ba hình nón có bán kính bằng nhau).

Một hình nón có bán kính đáy bằng \(5\)cm và diện tích xung quanh là \(65\pi \,{\rm{c}}{{\rm{m}}^{\rm{2}}}\). Tính thể tích của khối nón đó.

Nón lá là biểu tượng cho sự dịu dàng, bình dị, thân thiện của người Phụ nữ Việt Nam từ ngàn đời nay; nón lá Câu thơ là một đặc trưng của xứ Huế. Một chiếc nón lá hoàn thiện cần qua nhiều công đoạn từ lên rừng hái lá, rồi sấy lá, mở, ủi, chọn lá, xây độn vànhchằm, cắt lá, nức vành, cắt chỉ,… Nhằm làm đẹp và tôn vinh thêm cho chiếc nón lá xứ Huế, các nghệ nhân còn ép tranh và vài dòng thơ vào giữa hai lớp lá:

“Ai ra xứ Huế mộng mơ

Mua về chiếc nón Câu thơ làm quà”.

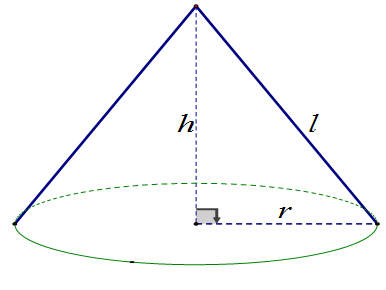
Khung của nón lá có dạng hình nón được làm bởi các thanh gỗ nối từ đỉnh tới đáy như các đường sinh (l), 16 vành nón được làm từ những thanh tre mảnh nhỏ, dẻo dai uốn thành những vòng tròn có đường kính to, nhỏ khác nhau, cái nhỏ nhất to bằng đồng xu.
– Đường kính \[\left( {d = 2r} \right)\] của chiếc nón lá khoảng 40 (cm);
– Chiều cao \(\left( h \right)\) của chiếc nón lá khoảng 19 (cm).
a) Tính độ dài của thanh tre uốn thành vòng tròn lớn nhất của vảnh chiếc nón lá.(không kể phần chắp nối, tính gần đúng đến 2 chữ số thập phân, biết\(\pi \approx 3,14\)).
b) Tính diện tích phần lá phủ xung quanhcủa chiếc nón lá. (không kể phần chắp nối,tính gần đúng đến 2 chữ số thập phân). Biết diện tích xung quanhcủa hình nón là \(S = \pi .R.l\).
Lời giải

Một đống cát có dạng hình nón có chu vi đáy là \(25,12\;{\rm{m}}\) và độ cao là \(1,5\;{\rm{m}}\).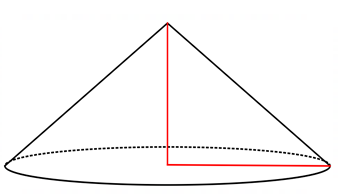

a) Tính thể tích của đống cát trên? Biết công thức tính chu vi đường tròn là \({\rm{C}} = 2\pi {\rm{R}}\) và công thức tính thể tích hình nón là \({\rm{V}} = \frac{1}{3}\pi {{\rm{R}}^2}\;{\rm{h}}\) (trong đó R là bán kính đường tròn đáy; h là chiều cao hình nón, lấy \(\pi = 3,14\) )
b) Người ta dùng xe cải tiến để vận chuyển đống cát đó đến khu xây dựng. Biết thùng chứa của xe cải tiến có dạng hình hộp chữ nhật có kích thước dài 1 m, rộng 6 dm và cao 3 dm. Trong mỗi chuyến xe, thùng xe có thể chứa nhiều hơn thể tích thực của nó là \(10\% \) để vận chuyển được nhiều cát hơn. Hỏi cần ít nhất bao nhiêu chuyến xe cải tiến để chuyển hết đống cát trên?

Bạn Nam dự định tổ chức buổi tiệc sinh nhật và chọn loại ly có phần chứa nước dạng hình nón với bán kính đáy \(R = 4\;{\rm{cm}}\) và độ dài đường sinh \(l = 10\;{\rm{cm}}\) để khách uống nước trái cây.

a) Tính thể tích phần chứa nước của ly (ghi kết quả làm tròn đến hàng đơn vị). Biết công thức thể tích hình nón là \(V = \frac{1}{3}\pi {{\rm{R}}^2}\;{\rm{h}}\) (với R là bán kính đáy hình nón; h là chiều cao hình nón).
b) Bạn Nam cần chuẩn bị một số hộp nước trái cây có lượng nước trong mỗi hộp là 1,2 lít. Biết rằng buổi tiệc sinh nhật có 14 người (đã bao gồm Nam). Nếu mỗi người trung bình uống 3 ly nước trái cây và lượng nước rót bằng \(90\% \) thể tích ly thì bạn Nam cần chuẩn bị ít nhất bao nhiêu hộp nước trái cây? Biết 1 lít \( = 1000\;{\rm{c}}{{\rm{m}}^3}\).

Một chiếc xô hình nón cụt làm bằng tôn để đựng nước. Các bán kính đáy là \(14{\rm{ }}\left( {{\rm{cm}}} \right)\) và \(9{\rm{ }}\left( {{\rm{cm}}} \right)\), chiều cao là \[23{\rm{ }}\left( {{\rm{cm}}} \right)\]. Tính dung tích của xô.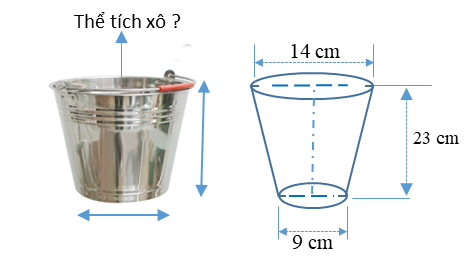

Một chiếc xô bằng tôn dạng hình nón cụt. Các bán kính đáy là \[12\] cm và \[8\] cm, chiều cao là \[24\] cm. Tính diện tích tôn để làm xô (không kể diện tích các chỗ ghép và xô không có nắp).

Người ta muốn làm một xô nước dạng chóp cụt như hình bên
a) Hãy tính diện tích tôn cần thiết để gò nên xô nước theo các kích thước đã cho (xem phần ghép mí không đáng kể)
b) Hỏi xô nước đã làm có thể chứa được tối đa bao nhiêu lít nước?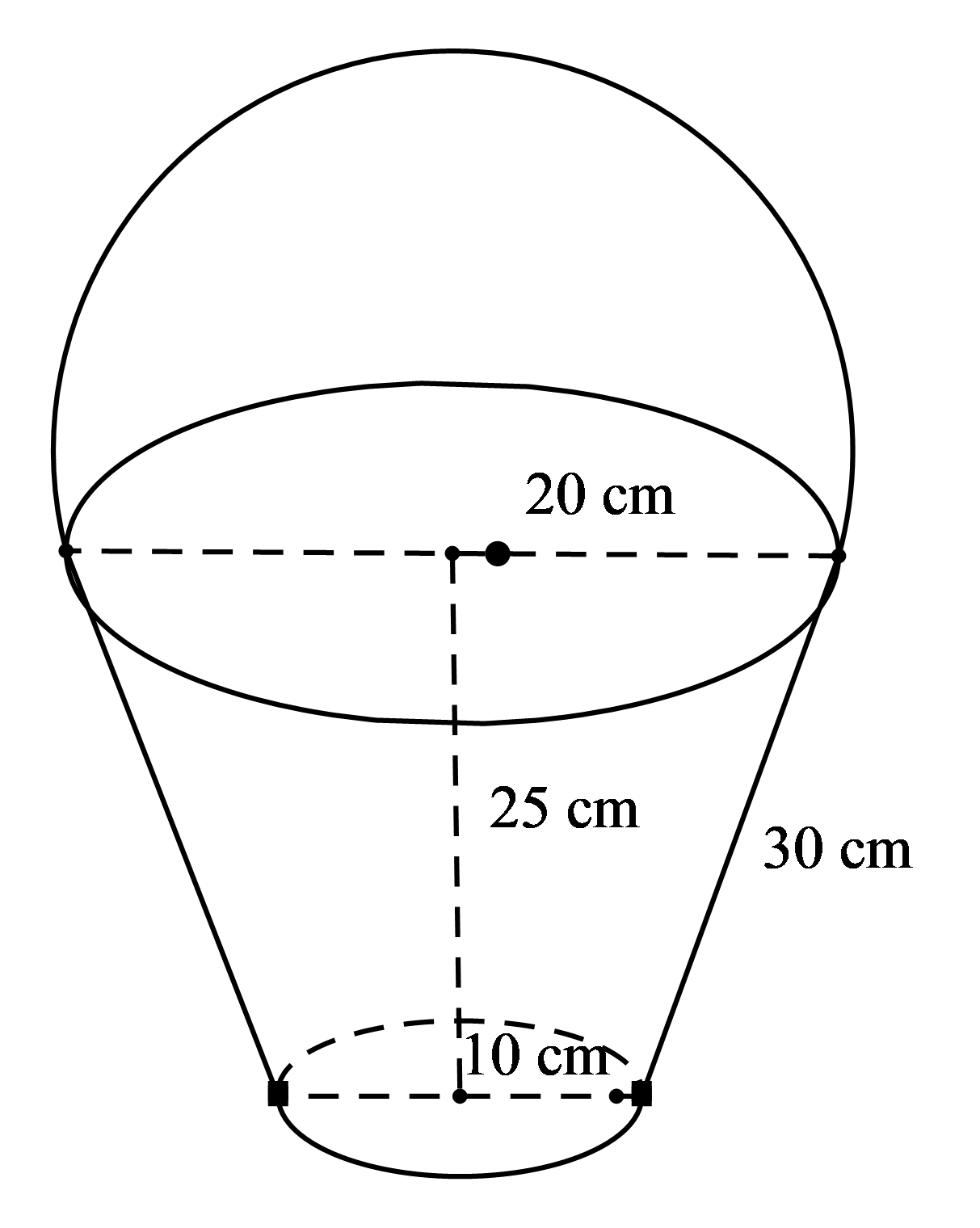

Một xô đựng nước có dạng hình nón cụt. Đáy xô có đường kính là\[28\,{\rm{cm}}\], miệng xô là đáy lớn của hình nón cụt có đường kính là\[36\,{\rm{cm}}\]. Hỏi xô có thể chứa bao nhiêu lít nước nếu chiều cao của xô là\[32\,{\rm{cm}}\]?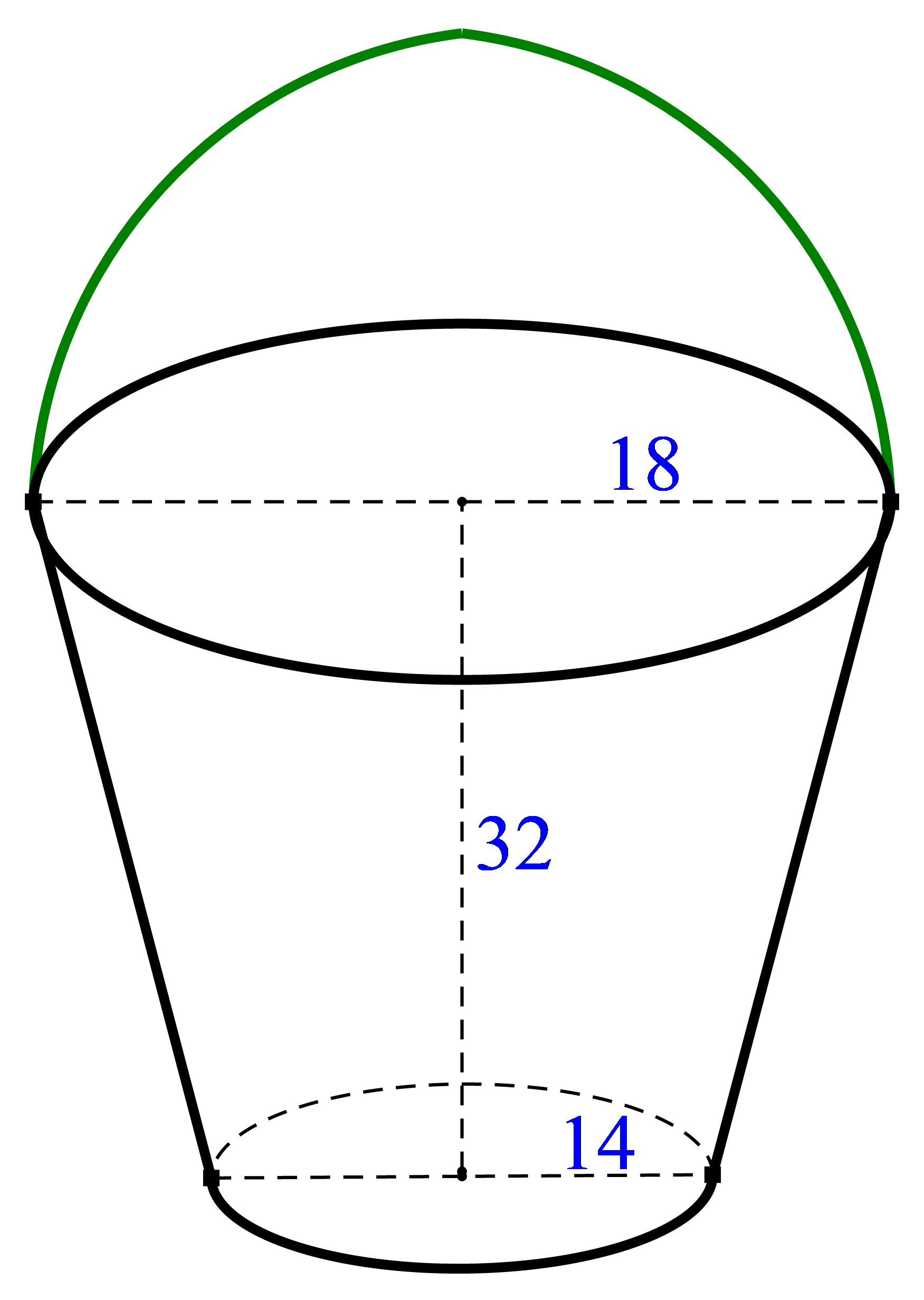

a) Người ta muốn làm một xô nước dạng hình nón cụt như hình bên, hãy tính diện tích tôn cần thiết để gò nên xô nước theo các kích thước đã cho (kể cả đáy). Cho biết phần ghép mí không đáng kể.
b) Hỏi xô nước đã làm có thể chứa được 25 lít nước không?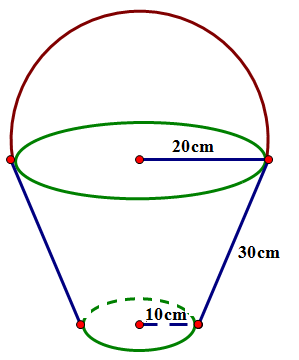Cho biết:- Diện tích xung quanh hình nón cụt: \({S_{xq}} = \pi .l.\left( {{r_1} + {r_2}} \right)\)- Thể tích hình nón cụt: \(V = \frac{1}{3}\pi .h.\left( {r_1^2 + r_2^2 + {r_1}{r_2}} \right)\)Với: \({r_1},{r_2}\) là các bán kính đáy; \(l\) là độ dài đường sinh; \(h\) là chiều cao.

Một xô đựng nước có dạng hình nón cụt (có các kích thước như hình). Đáy xô có đường kính là 20 cm, miệng xô là đáy lớn của hình nón cụt có đường kính 30 cm và chiều cao của xô là 22 cm.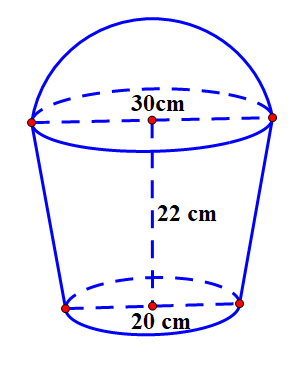

a) Xô có thể chứa tối đa bao nhiêu lít nước? Biết rằng thể tích của hình nón cụt có \[R,r,h\] lần lượt là bán kính đáy lớn, bán kính đáy nhỏ và chiều cao là: \(V = \frac{1}{3}\pi h\left( {{R^2} + Rr + {r^2}} \right)\) (kết quả làm tròn đến hàng đơn vị).
b) Bác Năm dùng hai xô nước để lấy nước từ một hồ để sử dụng trong sinh hoạt và trồng trọt. Gia đình bác sử dụng trung bình mỗi ngày 150 lít nước. Hỏi bác Năm cần phải lấy ít nhất bao nhiêu lần mỗi ngày (mỗi lần xách 2 xô) để phục vụ cho sinh hoạt và trồng trọt, biết rằng mỗi lần xách nước về thì lượng nước bị hao hụt khoảng \(5\% \).

Trong hình vẽ, 6 lon nước có dạng hình trụ được đặt sát nhau trong một thùng các-tông (carton) để bán. Đường kính và chiều cao của mỗi lon nước lần lượt là \(7cm\) và \(11cm\).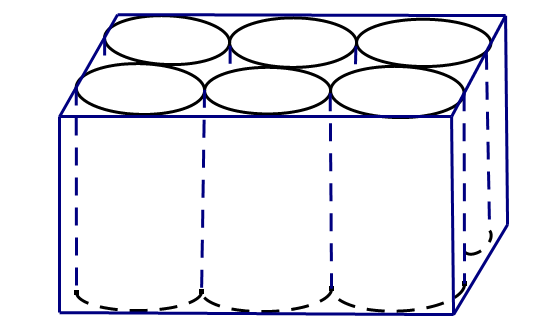a) Tìm thể tích của 6 lon nước.
b) Tính thể tích phần trống trong thùng các-tông khi đựng 6 lon nước (làm tròn đến đơn vị \({\rm{c}}{{\rm{m}}^3}\). Biết thể tích hình trụ được tính theo công thức: \({\rm{V}} = {{\rm{R}}^2}\pi \).h với R là bán kính đáy và h là đường cao của hình trụ)

Một nhà kính trồng rau sạch có dạng nửa hình trụ đường kính đáy là 30 m, chiều dài là 45 m. Người ta dùng màng nhà kính Politiv - Israel để bao quanh phần diện tích xung quanh nửa hình trụ và hai nửa đáy hình trụ. Khi thi công hao phí khoảng \(10\% \) diện tích nhà kính.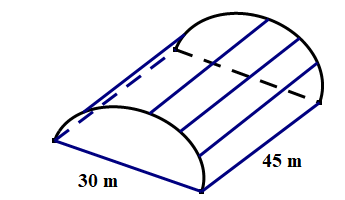a) Tính diện tích phần màng cần cho nhà trồng rau trên (làm tròn đến hàng đơn vị). Biết \({{\rm{S}}_{{\rm{xq}}}} = 2\pi {\rm{Rh}};{{\rm{S}}_{\rm{d}}} = \pi {{\rm{R}}^2}\), trong đó \({{\rm{S}}_{{\rm{xq}}}}\) là diện tích xung quanh của hình trụ \({{\rm{S}}_{\rm{d}}}\) là diện tích đáy của hình trụ, h là chiều cao hình trụ, \(R\) là bán kính hình trụ.
b) Tính chi phí cần có để mua màng làm kính trên biết rằng màng có khổ rộng \(2,2\;{\rm{m}}\) và dài 100 m có giá 13000 đồng \(/{{\rm{m}}^2}\) (chỉ bán theo cuộn).

Bạn An đi mua giúp bố cây lăn sơn ở cửa hàng nhà bác Toàn. Một cây lăn sơn tường có dạng một khối trụ với bán kính đáy là \(5cm\) và chiều cao là \(23cm\) (hình vẽ bên). Nhà sản xuất cho biết sau khi lăn 1000 vòng thì cây sơn tường có thể bị hỏng. Hỏi bạn An cần mua ít nhất mấy cây lăn sơn tường biết diện tích tường mà bố bạn An cần sơn là \(100\;{{\rm{m}}^2}\)?

Một ngôi biệt thự có 10 cây cột nhà hình trụ tròn, tất cả đều có chiều cao \(4,2\;{\rm{m}}\). Trong đó, 4 cây cột trước đại sảnh có đường kính 40 cm và 6 cây cột còn lại bên thân nhà có đường kính 26 cm. Chủ nhà dùng loại sơn giả đá để sơn 10 cây cột đó. Nếu giá của một loại sơn giả đá là 380000 đồng \(/{{\rm{m}}^2}\) (gồm cả tiền thi công) thì người chủ phải chi ít nhất bao nhiêu tiền để sơn 10 cây cột đó? (Số tiền làm tròn đến hàng nghìn).

a) Một bồn nước inox hình trụ nằm ngang có kích thước đường kính là \(1900mm\), chiều dài \(6300mm\) chứa được 15000 lít nước. Hỏi thể tích nước bằng bao nhiêu phần trăm thể tích bồn (làm tròn tới hàng đơn vị).
b) Hệ thống chữa cháy tự động Sprinkler (xem hình) khi nhiệt độ cháy sẽ làm những Sprinkler tự động phun nước chữa cháy, một Sprinkler bảo vệ cho phần diện tích tối đa là \(12\;{{\rm{m}}^2}\), lưu lượng tối thiểu cho một Sprinkler là 3456 lít/giờ. Theo tiêu chuẩn phòng cháy chữa cháy của Việt Nam thì 1 Sprinkler hoạt động tối thiểu trong 0,5 giờ. Giả sử tầng hầm tòa nhà chung cư Carina Plaza rộng \(1200\;{{\rm{m}}^2}\) thì chung cư cần bao nhiêu bồn inox ở câu a để trữ nước cho hệ thống chữa cháy?

Hộp phô mai hình trụ có đường kính đáy \(12,2\;{\rm{cm}}\), chiều cao \(2,4\;{\rm{cm}}\).

a) Biết rằng 8 miếng phô mai được xếp nằm sát nhau vừa khít trong hộp. Hỏi thể tích một miếng phô mai là bao nhiêu? (làm tròn kết quả đến chữ số thập phân thứ nhất)
b) Người ta gói từng miếng phô mai bằng một loại giấy đặc biệt. Giả sử phần giấy gói vừa khít miếng phô mai. Hãy tính diện tích phần giấy gói mỗi miếng phô mai. (Làm tròn kết quả đến hàng đơn vị).

Các ống hút nhựa thường khó phân hủy và gây hại cho môi trường. Mỗi ngày có 60 triệu ống hút thải ra môi trường gây hậu quả nghiêm trọng. Ngày nay người ta chủ động sản xuất các loại ống hút dễ phân hủy. Tại tỉnh Đồng Tháp có cơ sở chuyên sản xuất ông hút "thân thiện với môi trường" xuất khẩu ra thị trường thế giới và được nhiều nước ưa chuộng. Ông hút được làm từ bột gạo, các màu chiết xuất từ củ dền, lá dứa, bông sen, bông điên điển,.
Một ống hút hình trụ, đường kính 12 mm, bề dày ống 2 mm, chiều dài ống 180 mm. Em hãy tính xem để sản xuất mỗi ống thì thể tích bột gạo được sử dụng là bao nhiêu. (Biết thể tích hình trụ: \({\rm{V}} = \pi \cdot {{\rm{R}}^2}\).h với R là bán kính đáy và h là chiều cao; kết quả làm tròn đến chữ số thập phân thứ 2 với \(\pi \approx 3,14\) ).

Một cái chai có chứa một lượng nước, phần chứa nước là hình trụ có chiều cao 10 cm, khi lật ngược chai lại thì phần không chứa nước cũng là một hình trụ có chiều cao 8 cm (như hình vẽ bên). Biết thể tích của chai là \(1413\;{\rm{c}}{{\rm{m}}^3}\). Tính bán kính của đáy chai (giả sử độ dày của thành chai và đáy chai không đáng kể).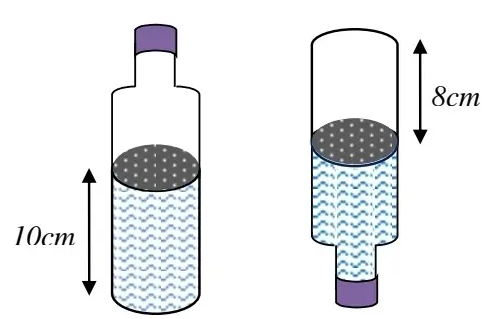

Có hai cốc thủy tinh hình trụ, cốc thứ nhất (hình A) có đường kính đáy là 30 cm, chiều cao 20 cm đựng đầy nước. Cốc thứ hai (hình B ) có đường kính đáy là 40 cm, chiều cao là 12 cm. Hỏi nếu đổ hết nước từ cốc thứ nhất sang cốc thứ hai nước có bị tràn ra ngoài hay không? Giải thích tại sao? (xem như bề dày của đáy cốc không đáng kể).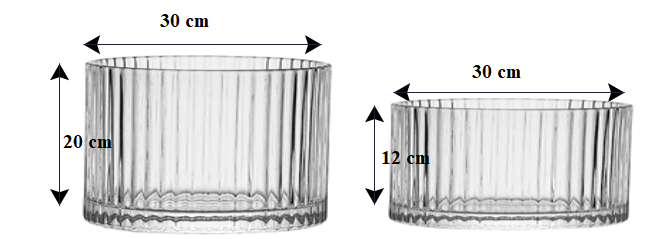

Hãy tính thể tích của bình chữa cháy bột 4 kg có dạng hình trụ, biết chiều cao \(49\;\left( {cm} \right)\) và diện tích toàn phần là \(784\pi \left( {c{m^2}} \right)?\)

Anh Minh vừa mới xây một cái hồ trữ nước cạnh nhà có hình hộp chữ nhật kích thước\(2\;{\rm{m}} \times 2\;{\rm{m}} \times 1\;{\rm{m}}\). Hiện hồ chưa có nước nên anh Minh phải ra sông lấy nước. Mỗi lần ra sông anh gánh được 1 đôi nước đầy gồm hai thùng hình trụ bằng nhau có kích thước đáy \(0,2\;{\rm{m}}\), chiều cao \(0,4\;{\rm{m}}\).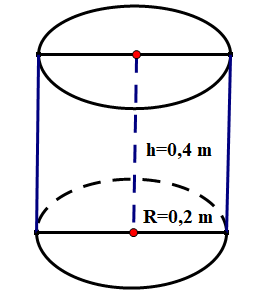a) Tính lượng nước \(\left( {{{\rm{m}}^3}} \right)\) anh Minh đổ vào hồ sau mỗi lần gánh (ghi kết quả làm tròn đến hai chữ số thập phân). Biết trong quá trình gánh nước về hao hụt khoảng \(10\% \) và công thức tính thể tích hình trụ là \({\rm{V}} = \pi {{\rm{R}}^2}\;{\rm{h}}\).
b) Hỏi anh Minh phải gánh ít nhất bao nhiêu lần để đầy hồ? Bỏ qua thể tích thành hồ.

Có hai lọ thủy tinh hình trụ, lọ thứ nhất phía bên trong có đường kính đáy là \(30cm\), chiều cao \(20cm\), đựng đầy nước. Lọ thứ hai bên trong có đường kính đáy là \(40cm\), chiều cao \(12cm\). Hỏi nếu đổ hết nước từ trong lọ thứ nhất sang lọ thứ hai nước có bị tràn ra ngoài không ? Tại sao ? (Lấy \(\pi \approx 3,14\))

Có hai lọ thủy tinh hình trụ, lọ thứ nhất phía bên trong có đường kính đáy là \[30\] cm, chiều cao \[20\] cm, đựng đầy nước. Lọ thứ hai bên trong có đường kính đáy là \[40\] cm, chiều cao \[12\] cm. Hỏi nếu đổ hết nước từ trong lọ thứ nhất sang lọ thứ hai nước có bị tràn ra ngoài không? Tại sao? (Lấy \(\pi \approx 3,14\)).

Có hai lọ thủy tinh hình trụ, lọ thứ nhất phía bên trong có đường kính đáy là \[30\] cm, chiều cao \[20\] cm, đựng đầy nước. Lọ thứ hai bên trong có đường kính đáy là \[40\] cm, chiều cao \[12\] cm. Hỏi nếu đổ hết nước từ trong lọ thứ nhất sang lọ thứ hai nước có bị tràn ra ngoài không? Tại sao? (Lấy \(\pi \approx 3,14\)).

Một bồn nước inox có dạng một hình trụ với chiều cao là \[1,65\]m và diện tích đáy là\[0,42{\rm{ }}{m^2}\]. Hỏi bồn nước này đựng đầy được bao nhiêu mét khối nước? (Bỏ qua bề dày của bồn nước).

Tính diện tích tôn cần thiết để làm một cái thùng hình trụ có chiều cao là \(80\)(cm) và đáy có diện tích là \(5024\)\(\left( {c{m^2}} \right)\) (không tính diện tích các chỗ mối ghép và nắp thùng). Lấy \(\pi = 3,14\).

Bạn Toán đi mua giúp bố cây lăn sơn ở cửa hàng nhà bác Học. Một cây lăn sơn tường có dạng một khối trụ với bán kính đáy là \(5{\rm{ cm}}\) và chiều cao là \(23{\rm{ cm}}\) (hình vẽ bên). Nhà sản xuất cho biết sau khi lăn \(1000\) vòng thì cây sơn tường có thể bị hỏng. Hỏi bạn Toán cần mua ít nhất mấy cây lăn sơn tường biết diện tích tường mà bố bạn Toán cần sơn là \(100{\rm{ }}{{\rm{m}}^2}\). (Cho \(\pi = 3,14\))

Tính diện tích tôn cần thiết để làm một cái thùng hình trụ có chiều cao là \(80\)(cm) và đáy có diện tích là \(5024\)\(\left( {c{m^2}} \right)\) (không tính diện tích các chỗ mối ghép và nắp thùng). Lấy \(\pi = 3,14\).

Một chai dung dịch rửa tay khô hình trụ cao \(12\)cm, đường kính đáy bằng \(5\)cm. Tính thể tích chai dung dịch đó.

Một lon coca chiều cao là \[11,7cm\]; bán kính đáy bằng \[3cm\]. Hỏi \[3\] lon coca như vậy có đổ đầy một chai 1 lít không? (lấy \(\pi \approx 3,14\) và làm tròn kết quả đến chữ số thập phân thứ nhất )

Một tàu đánh cá khi ra khơi cần mang theo \[50\] thùng dầu, mỗi thùng dầu coi là hình trụ có chiều cao là \[90\]cm, đường kính đáy thùng là \[60\]cm. Hãy tính xem lượng dầu tàu phải mang theo khi ra khơi là bao nhiêu lít (lấy \[\pi = 3,14\] kết quả làm tròn đến hàng đơn vị)?

Người ta làm một thùng chứa nước dạng hình trụ không có nắp bằng tôn. Diện tích tôn tối thiểu cần để làm thùng đó bằng \(5\pi \)\[{{\rm{m}}^{\rm{2}}}\] với \(\pi \approx 3,14\). Tính thể tích của thùng đó biết chiều cao của thùng bằng đường kính đáy (làm tròn đến hai chữ số thập phân).

Lon nước ngọt hình trụ có đường kính đáy là \(5\) cm, chiều cao là \(12\) cm. Tính thể tích lon nước ngọt? (làm tròn kết quả đến chữ số thập phân thứ 2 và lấy \(\pi \approx 3,14\))

Một chiếc cốc hình trụ có đường kính đáy là \(10\) cm, chiều cao bằng \(\frac{6}{5}\) đường kính đáy. Tính thể tích của chiếc cốc đó.

Một téc nước hình trụ mà phía trong có đường kính đáy là \(0,6\,m\) chiều cao \(1\,m\). Tính thể tích nước chứa đầy trong 45 téc như vậy.

Một lon nước ngọt hình trụ có đường kính đáy là \(5\) cm, độ dài trục là \(12\)cm. Tính diện tích toàn phần của lon nước hình trụ đó.

Một chiếc cốc thủy tinh hình trụ có đường kính đáy là 6 cm, chiều cao 12 cm. Tính lượng nước chứa được khi rót nước đầy cốc.

Một hộp sữa hình trụ có bán kính đáy là 4cm, chiều cao là 10cm. Tính diện tích vật liệu dùng để tạo nên một vỏ hộp hộp sữa đó nếu tỉ lệ hao hụt là 5%?

Một hộp sữa hình trụ có đường kính đáy là\[12{\rm{ cm}}\], chiều cao là\[10{\rm{ cm}}\]. Tính diện tích vật liệu dùng để tạo nên vỏ hộp như vậy. (Không tính phần mép nối).

Người ta nhấn chìm hoàn toàn một tượng đá nhỏ vào một lọ thủy tinh có dạng hình trụ. Diện tích đáy lọ thủy tinh là \(21,6\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\). Nước trong lọ dâng lên \(9,5\,{\rm{mm}}\). Hỏi thể tích của tượng đá là bao nhiêu?

Một bồn hình trụ đang chứa dầu, được đặt nằm ngang, có chiều dài bồn là \(5m\), có bán kính đáy \(1m\), với nắp bồn đặt trên mặt nằm ngang của mặt trụ. Người ta đã rút dầu trong bồn tương ứng với \(0,5m\) của đường kính đáy. Tính thể tích gần đúng nhất của khối dầu còn lại trong bồn (lấy \(\pi \approx 3,14\), kết quả làm tròn đến chữ số thập phân thứ hai, theo đơn vị \({m^3}\))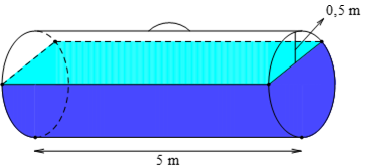 

Một hình trụ có bán kính đường tròn đáy là 6 cm, chiều cao 9 cm. Hãy tính diện tích xung quanh của hình trụ.

Một bể nước hình trụ có chiều cao 2,5 m và diện tích đáy là 4,8 m2. Nếu một vòi nước được đặt phía trên miệng bể và chảy được 4800 lít nước mỗi giờ thì sau bao lâu bể đầy? (Biết ban đầu bể cạn nước và bỏ qua bề dày của thành bể).

Một cây lăn sơn tường có dạng là một khối trụ với bán kính đáy là 5cm và chiều cao (chiều dài lăn) là 30 cm. Nhà sản xuất cho biết sau khi lăn 500 vòng thì cây sơn tường có thể sẽ bị hỏng. Tính diện tích mà cây sơn tường sơn được trước khi hỏng.

Một chiếc cốc có dạng hình trụ với chiều cao \(8\,{\rm{cm}}\), bán kính đáy là \(3\,{\rm{cm}}\). Hỏi chiếc cốc này có đựng được \(180\,{\rm{ml}}\) sữa không? (Bỏ qua bề dày của chiếc cốc).

Một hộp phomai con bò cười gồm có \(8\)miếng, độ dày mỗi miếng là \(20\,{\rm{mm}}\), nếu xếp chúng lại trên một đĩa thì thành hình trụ có đường kính \(100\,{\rm{mm}}\).
a) Tính thể tích của miếng phomai.
b) Biết khối lượng của mỗi miếng phomai là \(15\,{\rm{g}}\), hãy tính trọng lượng riêng của nó? (làm tròn kết quả đến hàng đơn vị)
(Biết trọng lượng riêng của vật cho bởi công thức \(d = \frac{P}{V}\). Trong đó trọng lượng của vật là \(P = 9,8.\,m\), đơn vị \(N\),với \(m\) là khối lượng vật đơn vị \({\rm{kg}}\); \(V\) là thể tích vật, đơn vị \({m^3}\); \(d\) có đơn vị \(N/{m^3}\)).

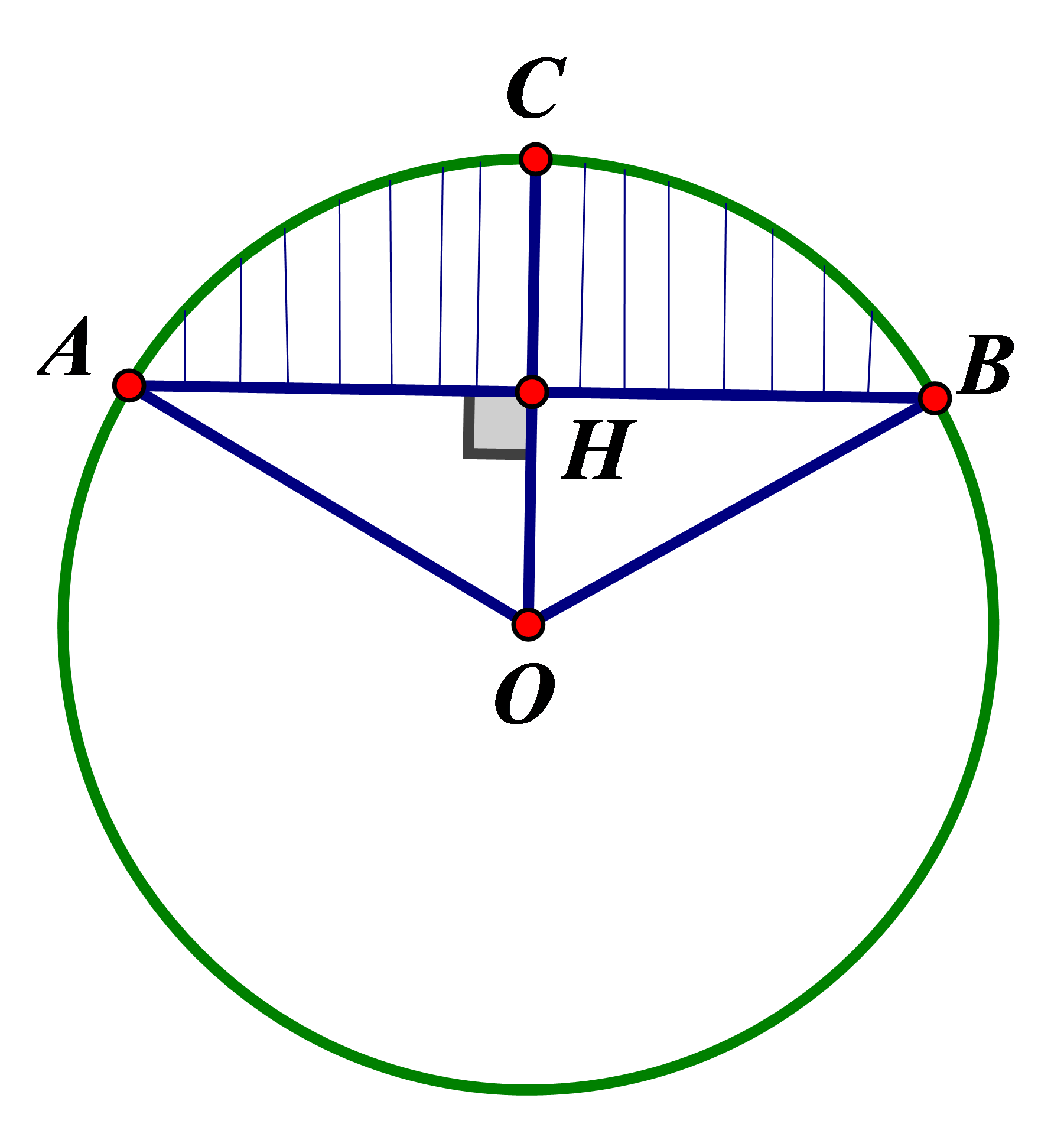
Một cái bánh hình trụ có bán kính đường tròn đáy là 3cm, chiều cao 4cm được đặt thẳng đứng trên mặt bàn. Một phần của cái bánh bị cắt rời ra theo các bán kính OA, OB và theo chiều thẳng đứng từ trên xuống dưới với $\widehat{AOB}={30}^0$. Tính thể tích phần còn lại của cái bánh sau khi cắt.

Một mẫu pho mát được cắt ra từ một khối pho mát dạng hình trụ (có các kích thước như trên hình vẽ). Tính theo gam khối lượng của mẫu pho mát biết khối lượng riêng của pho mát là \(3g/c{m^3}\).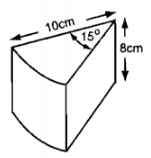

Một hộp thực phẩm có hình trụ. Biết diện tích của đáy là 60,24 \(c{m^2}\).
a) Hãy tính bán kính của đường tròn đáy của hình trụ. Biết \(\pi \approx 3,14\).
b) Biết chiều cao của hình trụ là 5cm. Hãy tính thể tích của hộp thực phẩm.

Một cốc nước hình trụ cao 15cm, đường kính đáy là 6cm. Lượng nước ban đầu cao 10cm. Thả vào cốc 5 viên bi hình cầu cùng đường kính 2cm. Hỏi sau khi thả 5 viên bi mực nước cách miệng cốc bao nhiêu cm? (Làm tròn lấy 2 chữ số thập phân).

Khi thả chìm hoàn toàn tượng một con ngựa nhỏ bằng đá vào một ly nước có dạng hình trụ thì người ta thấy nước trong ly dâng lên \(1,5\,{\rm{cm}}\) và không tràn ra ngoài. Biết diện tích đáy của ly nước bằng \[80{\rm{ c}}{{\rm{m}}^2}.\] Hỏi thể tích của tượng ngựa đá bằng bao nhiêu?

Các ống hút nhựa thường khó phân hủy và gây hại cho môi trường. Mỗi ngày có 60 triệu ống hút thải ra môi trường gây hậu quả nghiêm trọng. Ngày nay người ta chủ động sản xuất các loại ống hút dễ phân hủy. Tại tỉnh Đồng Tháp có cơ sở chuyên sản xuất ống hút “thân thiện với môi trường” xuất khẩu ra thị trường thế giới và được nhiều nước ưa chuộng. Ống hút được làm từ bột gạo, các màu chiết xuất từ củ dền, lá dứa, bông sen, bông điên điển,…Một ống hút hình trụ, đường kính 12mm, bề dày ống 2mm, chiều dài ống 180mm. Em hãy tính xem để sản xuất mỗi ống thì thể tích bột gạo được sử dụng là bao nhiêu (Biế\[\pi \approx 3,14\])

Một cái bánh hình trụ có bán kính đường tròn đáy là \[5cm,\] chiều cao \[9cm,\] được đặt thẳng đứng trên một mặt bàn. Một phần của cái bánh đã bị cắt rời ra theo các bán kính \[OA,\]\[OB\] và theo chiều thẳng đứng từ trên xuống với góc \[AOB\] bằng như hình vẽ. Tính thể tích phần còn lại của cái bánh sau khi bị cắt.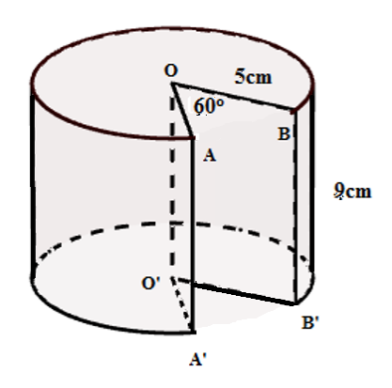

Nước giải khát thường đựng trong lon nhôm và cỡ lon phổ biến chứa được khoảng \(330\,ml\) chất lỏng, được thiết kế hình trụ với chiều cao khoảng \(10,2\,cm\) (phần chứa chất lỏng), đường kính đáy khoảng \(6,42\,cm\).
Nhưng hiện nay các nhà sản xuất có xu hướng tạo ra những lon nhôm với kiểu dáng cao thon hơn. Tuy chi phí sản xuất những chiếc lon cao này tốn kém hơn, nhưng nó lại dễ đánh lừa thị giác và được người tiêu dùng ưa chuộng hơn.
a/ Một lon nước ngọt cao \(13,41\,cm\) (phần chứa chất lỏng), đường kính đáy là \(5,6\,cm\). Hỏi lon nước ngọt cao này có thể chứa được hết lượng nước ngọt của một lon có cỡ phổ biến không? Vì sao? (Biết thể tích hình trụ: \(V = \pi {r^2}h\), với \(\pi \approx 3,14\)).
b/ Vì sao chi phí sản xuất chiếc lon cao tốn kém hơn chiếc lon cỡ phổ biến?
Biết diện tích xung quanh, diện tích toàn phần hình trụ được tính theo công thức:
\({S_{xq}} = 2\pi rh\) và \({S_{tp}} = {S_{xq}} + 2{S_{\~n a\`u y}}\).

Thùng phuy (hay thùng phi) là một vận dụng hình ống dùng để chứa và chuyên chở chất lỏng với dung tích lớn. Mỗi thùng phuy có đường kính nắp và đáy là\[584{\kern 1pt} {\kern 1pt} {\kern 1pt} mm\], chiều cao là \[876{\kern 1pt} {\kern 1pt} {\kern 1pt} mm\]. Hãy tính diện tích xung quanh, diện tích toàn phần và thể tích của một thùng phuy? (Biết công thức tính diện tích xung quanh là\[{{\bf{S}}_{{\bf{xq}}}} = 2\pi rh\], diện tích toàn phần là và thể tích hình trụ là \[V = \pi {r^2}h\], với \(\pi \approx 3,14\)).

Có hai lọ thủy tinh hình trụ, lọ thứ nhất phía bên trong có đường kính đáy là \(30\)cm, chiều cao \(20\)cm đựng đầy nước, lọ thứ hai bên trong có đường kính đáy là \(40\)cm chiều cao là\(12\)cm. Hỏi nếu đổ hết nước từ lọ thứ nhất sang lọ thứ hai nước có bị tràn ra ngoài hay không? Tại sao?

Khi thả chìm hoàn toàn một viên xúc xắc nhỏ hình lập phương vào một ly nước có dạng hình trụ thì người ta thấy nước trong ly dâng lên \(0,5\;{\rm{cm}}\) và không tràn ra ngoài. Biết diện tích đáy của ly nước bằng \(250\;{\rm{c}}{{\rm{m}}^2}\). Hỏi cạnh của viên viên xúc xắc dài bao nhiêu cm?

Nước giải khát thường đựng trong lon nhôm và cỡ lon phổ biến chứa được khoảng 330 ml chất lỏng, được thiết kế hình trụ với chiều cao khoảng \(10,2\;cm\); đường kính đáy khoảng \(6,42\;cm\). Nhưng hiện nay các nhà sản xuất có xu hướng tạo ra những lon nhôm với kiểu dáng cao thon hơn. Tuy chi phí sản xuất những chiếc lon cao này tốn kém hơn, nhưng nó lại dễ đánh lừa thị giác và được người tiêu dùng ưa chuộng hơn.
a) Một lon nước ngọt cao \(13,41\;cm\), đường kính đáy là \(5,6\;cm\). Hỏi lon nước ngọt cao này có thể chứa được hết lượng nước ngọt của một lon có cỡ phổ biến không? Vì sao?
Biết thể tích hình trụ: \(V = \pi {r^2}\;h\), với \(\pi \approx 3,14\).
b) Biết chi phí sản xuất một chiếc lon tỉ lệ thuận với diện tích toàn phần của lon. Hỏi chi phí sản xuất chiếc lon cao tăng bao nhiêu phần trăm so với chi phí sản xuất chiếc lon cỡ phổ biến? (làm tròn 1 chữ số thập phân). Biết diện tích xung quanh, diện tích toàn phần hình trụ được tính theo công thức: \({S_{xq}} = 2\pi rh{\rm{ }}v\`a {\rm{ }}{S_\varphi } = {S_{xq}} + 2\;{S_{{\rm{d }}}}\).

Bún bò Huế là một đặc sản của ẩm thực Huế, tuy là bún bò nhưng ngoài thịt bò còn có thịt heo. Hương vị đặc biệt của món ăn này chủ yếu là ở vị cay nồng, mùi sả đặc trưng của nước lèo. Vốn là một hương vị Huế không lẫn vào đâu được và chính điều đó khiến người ăn cứ nhớ mãi về món ăn này. Quán nhà bạn An dùng 2 chiếc nồi hình trụ có bán kính đáy nồi là \(0,3\;m\), chiều cao nồi là \(0,8\;m\) để nấu nước lèo bún bò Huế. Sau khi vớt xương và các gia vị thì lượng nước lèo trong nồi chiếm \(90\% \) thể tích nồi.
a) Tính thể tích mỗi nồi nước lèo nhà bạn An nấu, biết lượng nước lèo ở mỗi nồi là như nhau (ghi kết quả đến \(c{m^3}\)).
b) Đề bán bún bò, mỗi lần bán 1 tô bún mẹ bạn An dùng cái vá có dạng nửa hình cầu bán kính \(6,5\;cm\) và múc đúng 1 vá cho mỗi tô. Hỏi sau khi bán hết bún bò thì quán nhà bạn An thu được bao nhiêu tiền? Biết giá 1 tô bún bò là 35000 đồng. Biết công thức tính thể tích hình trụ là \(V = 3,14.{r^2}\;h\) và công thức tính thể tích hình cầu là \(V = \frac{4}{3}.3,14.{R^3}\).

Một xe chở xăng dầu, bên trên có một bồn chứa hình trụ dài \(2,6\;m\)và đường kính đáy là \(1,4\;m\). Theo tiêu chuẩn an toàn thì bồn chi chứa được tối đa \(80\% \) thể tích khi xe di chuyển trên đường.
a) Mỗi chuyến xe có thể chở nhiều nhất bao nhiêu lít nhiên liệu? (cho \(\pi = 3,14\)).
b) Trên đường vận chuyển, xe chở xăng dầu trên phải đi qua 1 cây cầu có tải trọng 5 tấn. Biết xe khi chưa chở hàng nặng 3 tấn. Hỏi nếu muốn đi qua cây cầu đó thì xe chở tối đa bao nhiêu lít xăng? Biết khối lượng riêng của xăng là \(0,713\;kg/\)lít (Các kết quả làm tròn đến hàng đơn vị).

Một tháp nước có bể chứa là một hình cầu, đường kính bên trong của bể đo được là 6 mét. Người ta dự tính lượng nước đựng đầy trong bể đủ dùng cho một khu dân cư trong 5 ngày. Cho biết khu dân cư đó có \(1304\) người. Hỏi người ta đã dự tính mức bình quân mỗi người dùng bao nhiêu lít nước trong một ngày? (Lấy \(\pi \approx 3,14\), kết quả làm tròn đến chữ số thập phân thứ nhất)

Một viên bi sắt hình cầu có bán kính bằng 5cm, tính thể tích của viên bi đó.( Kết quả làm tròn đến 2 chữ số thập phân ) (Lấy \[\pi \]\( \approx 3,14\)).

Cần phải có ít nhất bao nhiêu lít nước để thay nước cho một chậu thủy tinh nuôi cá cảnh? (Chậu nước được xem như một phần mặt cầu đường kính \(3\,dm\)). Biết lượng nước đổ vào chiếm \(\frac{2}{3}\) thể tích hình cầu và 1 lít \( = 1\,d{m^3}\).

Tính diện tích da dùng để làm quả bóng hình cầu nếu không tính đến tỉ lệ hao hụt. Biết khi bơm căng thì quả bóng có đường kính là 14 cm.

Tính thể tích không khí \[\left( {k{m^3}} \right)\] trong tầng đối lưu của trái đất biết rằng bán kính trái đất là khoảng 6371 km và tầng đối lưu được tính từ mặt đất cho đến khoảng 10 km so với mặt đất.( làm tròn đến \[k{m^3}\])?

Một lọ nước hoa có hình dạng bên ngoài là hình cầu làm bằng thuỷ tinh có đường kính 8 cm. Lòng bên trong của lọ cũng là một hình cầu nhỏ cùng tâm với hình cầu bên ngoài để chứa nước hoa. Hỏi phải làm lọ nước hoa có độ dày thành lọ là bao nhiêu cm để chứa được lượng nước hoa bên trong là 120 ml? (làm tròn đến hàng phần mười). Biết rằng lượng nước hoa được chứa trong lọ chiếm \(80\% \) thể tích của phần có thể chứa nước hoa.

Một quả bóng bàn dạng một hình cầu có bán kính bằng 2 cm. Tính diện tích bề mặt của quả bóng bàn đó ( lấy \[\pi \approx 3,14\]).

Một quả bóng bằng da có đường kính \(22cm\). Tính diện tích da cần dùng để làm quả bóng nếu không tính tỉ lệ hao hụt (lấy \[\pi = 3,14\]).

Trái Đất, hành tinh chúng ta đang sống, dạng hình cầu có bán kính là \(6370{\rm{ }}km\). Biết rằng \(29\% \) diện tích bề mặt Trái Đất không bị bao phủ bởi nước bao gồm núi, sa mạc, cao nguyên, đồng bằng và các địa hình khác. Tính diện tích bề mặt mặt Trái Đất bị bao phủ bởi nước. (Lấy \(\pi = 3,14\), kết quả làm tròn đến chữ số hàng đơn vị).

Ngày 4-6-1783, anh em nhà Mông-gôn-fi-ê (người Pháp) phát ra khinh khí cầu dùng không khí nóng. Coi khinh khí cầu này là hình cầu có đường kính \(11m\) và được làm bằng vải dù để là khinh khí cầu đó (lấy \(\pi \approx 3,14\) và làm tròn đến chữ số thập phân thứ hai).

Một tháp nước có bể chứa hình cầu, đường kính bên trong của bể đo được là 6m
a) Tính thể tích của tháp nước đó?
b) Người ta dự tính lượng nước đựng đầy trong bể đủ dùng cho một khu dân cư trong 5 ngày. Cho biết khu dân cư đó có 1304 người. Hỏi người ta đã dự tính mức bình quân mỗi người dùng bao nhiêu lít nước trong một ngày? (Lấy π≈3,14, kết quả làm tròn đến chữ số thập phân thứ nhất).

Một quả pha lê hình cầu có diện tích mặt cầu bằng \[144\pi \,c{m^2}\]. Tính thể tích quả pha lê đó.

Giả sử một quả dưa hấu không hạt ruột đỏ dạng hình cầu có đường kính \(25cm\) và phần vỏ dày \(2cm\).
a) Coi phần ruột màu đỏ cũng có dạng hình cầu và đặc. Thể tích phần ruột màu đỏ chiếm bao nhiêu phần trăm thể tích quả dưa hấu? (Kết quả làm tròn tới chữ số thập phân thứ hai).
Cho biết công thức tính thể tích hình cầu là \({\rm{V}} = \frac{4}{3}\pi {{\rm{R}}^3}\), với R là bán kính hình cầu, \(\pi = 3,14\).
b) Người ta ép phần ruột màu đỏ của quả dưa hấu trên thì thể tích nước ép thu được bằng \(80\% \) thể tích phần ruột. Nước ép dưa hấu được đựng trong một một ly thủy tinh, phần lòng trong dạng hình trụ có chiều cao 10 cm và đường kính đáy lòng trong là\(5cm\). Mỗi ly chỉ chứa \(70\% \) nước ép dưa hấu. Hỏi dùng nước ép của một quả dưa hấu nói trên thì làm ra bao nhiêu ly nước ép dưa hấu? (kết quả làm tròn đến hàng đơn vị).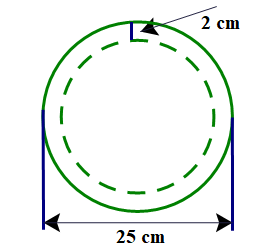

Hình bên là một mẫu pho mát được cắt ra từ một khối pho mát dạng hình trụ (có các kích thước như hình vẽ). Biết khối lượng riêng của pho mát là \(3\;{\rm{g}}/{\rm{c}}{{\rm{m}}^3}\) và công thức khối lượng riêng là \({\rm{D}} = \frac{{\rm{m}}}{{\rm{V}}}\) (Trong đó \({\rm{D}}\left( {{\rm{g}}/{\rm{c}}{{\rm{m}}^3}} \right)\) là khối lượng riêng, \({\rm{m}}({\rm{g}})\) là khối lượng, \({\rm{V}}\left( {{\rm{c}}{{\rm{m}}^3}} \right)\) là thể tích).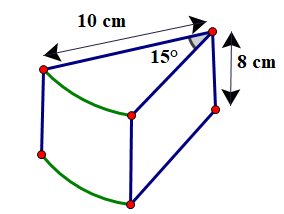

a) Hãy tính diện tích 1 mặt đáy và khối lượng của mẫu pho mát trên. Biết thể tích hình trụ \({{\rm{V}}_{{\rm{tru }}}} = {\rm{S}}\).h. Trong đó S là diện tích 1 đáy và h là chiều cao của hình trụ.
b) Chiếc hộp thực phẩm hình hộp chữ nhật có kích thước lần lượt là \(189\;{\rm{mm}},103\;{\rm{mm}},101\;{\rm{mm}}\) (xem hình bên) có thể chứa hết phần còn lại của khối pho mát không?

Một khối gỗ hình lập phương cạnh 8 cm, được khoét bởi một hình nón, đường sinh \({\rm{AB}} = 8,6\;{\rm{cm}}\). và đỉnh chạm mặt đáy của khối gỗ (xem hình bên). Hãy tính bán kính đáy của hình nón và thể tích của khối gỗ còn lại. Biết \({{\rm{V}}_{{\rm{lap phuong }}}} = {{\rm{a}}^3}\) (a là cạnh hình lập phương); \({{\rm{V}}_{{\rm{hinh n\'o n }}}} = \frac{1}{3}\pi {{\rm{R}}^2}\;{\rm{h}}({\rm{R}} = {\rm{OB}}\) là bán kính mặt đáy, \({\rm{h}} = {\rm{OA}}\) là chiều cao của hình nón \();\pi \approx 3,14\).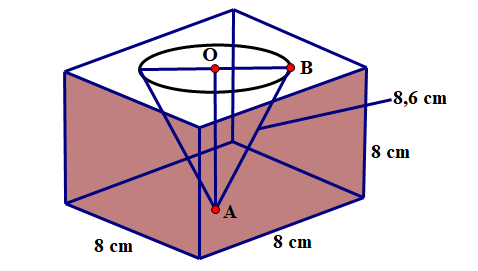

Một xe bồn chở nước sạch cho một khu dân cư có 200 hộ dân. Bồn xe có hình dạng và kích thước như hình vẽ bên dưới, mỗi đầu của bồn xe là nửa hình cầu. Xe chở đầy nước và lượng nước chia đều cho từng hộ dân. Tính xem mỗi hộ dân được nhận bao nhiêu lít nước sạch.

Một hãng sản xuất rượu vang đã đặt hàng một công ty sản xuất thủy tinh một kiểu ly có phần đựng rượu cao 6 cm, đường kính miệng ly là 6 cm. Biết rằng để tạo thành một cái ly là sự kết hợp gồm thành ly là một hình trụ cao 3 cm, phần đáy ly là một nửa khối cầu có đường kính bằng với đường kính của miệng ly.
a) Hãy tính thể tích rượu được chứa tối đa khi đổ vào ly? Cho biết: \({{\rm{V}}_{{\rm{tru}}}} = \pi {{\rm{r}}^2}\;{\rm{h}}\) với r là bán kính đáy; h là chiều cao hình trụ. \({{\rm{V}}_{{\rm{cau }}}} = \frac{4}{3}\pi {{\rm{R}}^3}\) với R là bán kính hình cầu.
b) Ông A cần chuẩn bị một số chai rượu vang, lượng rượu trong mỗi chai là 0,85 lít. Biết rằng trong bữa tiệc có 12 người ( bao gồm luôn ông A ), mỗi người uống 4 ly rượu, lượng rượu được rót bằng \(60\% \) thể tích của ly. Ông A cần chuẩn bị ít nhất bao nhiêu chai rượu vang?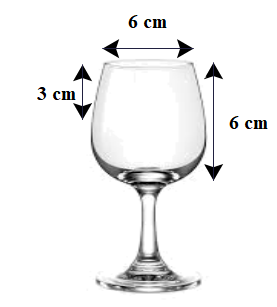

Một chiếc đồng hồ cát bằng thủy tinh có dạng hình trụ, phần chứa cát là hai nửa hình cầu bằng nhau (Hình vẽ bên với các kích thước đã cho là bản thiết kế thiết diện qua trục của chiếc đồng hồ này, giả sử phần thông nhau không đáng kể). Khi đó, lượng thủy tinh làm chiếc đồng hồ cát là bao nhiêu? (làm tròn đến chữ số thập phân thứ hai).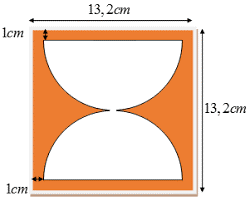

Cối xay gió của Đôn-ki-hô-tê có dạng một hình nón. Chiều cao của hình nón là 42 cm và thể tích của nó là \(17600\;{\rm{c}}{{\rm{m}}^3}\). Em hãy giúp chàng Đôn-ki-hô-tê tính:
a) Bán kính của hình nón.
b) Diện tích gạch cần để xây ngôi nhà hình trụ bên dưới, biết nhà có chiều cao 250 cm. Làm tròn kết quả đến chữ số thập phân thứ nhất với đơn vị đề-xi-mét. 

Một bình nước hình hộp chữ nhật có chiều rộng, chiều dài đáy bình và chiều cao lần lượt tỉ lệ với \(2;3\) và 5. Biết chiều cao của bình là 20 cm.
a) Tính thể tích nước tối đa mà bình chứa được.
b) Bình nước được rót ra các ly hình trụ có đường kính đáy là 5 cm, chiều cao 12 cm. Biết bình đựng đầy nước và rót vào ly \(90\% \) thể tích của ly. Tính số ly nước chứa hết số nước từ bình.

Một cốc thủy tinh hình trụ đựng đầy nước có chiều cao bằng 10 cm và thể tích bằng \(90\pi {\rm{c}}{{\rm{m}}^3}\). Người ta thả vào cốc một viên bi sắt hình cầu có bán kính bằng bán kính đáy cốc nước, viên bi sắt ngập toàn bộ trong nước. Tính lượng nước bị tràn ra khỏi cốc? (làm tròn kết quả đến chữ số thâp phân thứ nhất).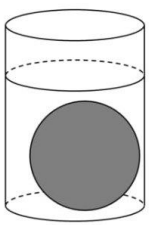

Một cốc nước hình trụ có chiều cao \(15cm\), bán kính đáy là \(3cm\) và lượng nước ban đầu trong cốc cao \(12cm\). Thả chìm hoàn toàn vào cốc nước 3 viên bi thủy tinh hình cầu có cùng bán kính là \(2cm\). (Giả sử độ dày của thành cốc và đáy cốc không đáng kể - mô phỏng bằng hình vẽ)
a) Tính thể tích của nước trong cốc.
b) Khi thả 3 viên bi hình cầu vào cốc thì nước trong cốc có bị tràn ra ngoài không? Nếu có hãy tính thể tích nước bị tràn ra ngoài?
(Biết công thức tính thể tích của hình trụ là \({\rm{V}} = \pi {{\rm{r}}^2}\;{\rm{h}}\), thể tích hình cầu là \({\rm{V}} = \frac{4}{3}\pi {{\rm{R}}^3}\), lấy \(\pi = 3,14\) các kết quả làm tròn đến chữ số thập phân thứ 2 )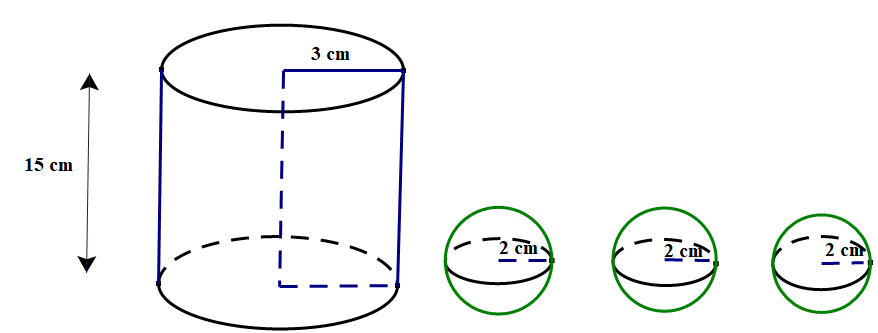

Một cái mũ như hình bên, gồm một hình nón và một hình vành khăn. Tính diện tích vải cần dùng để tạo ra bề mặt bên ngoài của cái mũ. Biết công thức tính diện tích xung quanh của hình nón là \({\rm{S}} = \pi {\rm{r}}l\) ( r là bán kính đáy hình nón, \(l\) là độ dài đường sinh hình nón), công thức tính diện tích hình vành khăn là \({\rm{S}} = \pi \left( {{{\rm{R}}^2} - {{\rm{r}}^2}} \right)\) ( R là bán kính đường tròn lớn, \(r\) là bán kính đường tròn nhỏ) và diện tích vải bị hao hụt khi may nón là \(17\% \) (kết quả làm tròn đến hàng đơn vị).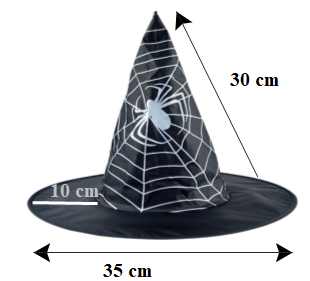

Cho hình bên là một thúng gạo vun đầy. Thúng có dạng nửa hình cầu với đường kính 50 cm, phần gạo vun lên có dạng hình nón cao 15 cm.a) Tính thể tích phần gạo trong thúng (làm tròn đến dạng 0,1 ).
Biết thể tích hình nón là \({\rm{V}} = \frac{1}{3}\pi {{\rm{R}}^2}\;{\rm{h}}\), hình trụ là \({\rm{V}} = \pi {{\rm{R}}^2}\;{\rm{h}}\) và hình cầu là \({\rm{V}} = \frac{4}{3}\pi {{\rm{R}}^3}\)
b) Nhà Danh dùng lon sữa bò cũ có dạng hình trụ (bán kính đáy bằng 5 cm, chiều cao 15 cm ) để đong gạo mỗi ngày. Biết mỗi ngày nhà Danh ăn 5 lon gạo và mỗi lần đong thì lượng gạo chiếm \(90\% \) thể tích lon. Hỏi với lượng gạo ở thúng trên thì nhà Danh có thể ăn nhiều nhất là bao nhiêu ngày.

Một chai nước suối của hãng A được thiết kế gồm ba phần: phần miệng chai có dạng hình trụ với chiều cao \(2,5\;{\rm{cm}}\) và đường kính đường tròn đáy là 3 cm, phần cổ chai có dạng hình nón cụt với chiều cao 5 cm, phần thân chai có dạng hình trụ với chiều cao 10 cm và đường kính đường tròn đáy là 6 cm (như hình vẽ).
a) Tính thể tích của chai nước (làm tròn đến hàng đơn vị). Biết thể tích hình trụ là \(V = \pi {{\rm{R}}^2}h\) với R là bán kính đường tròn đáy, \(h\) là chiều cao hình trụ, thể tích hình nón cụt là \({\rm{V}} = \frac{1}{3}\pi {\rm{h'}}\left( {{\rm{r}}_1^2 + {\rm{r}}_2^2 + {{\rm{r}}_1}{{\rm{r}}_2}} \right)\) với \({{\rm{r}}_1},{{\rm{r}}_2}\) là hai bán kính đường tròn đáy của hình nón cụt, h' là chiều cao của hình nón cụt.
b) Người ta đóng nước vào chai và để tránh tình trạng dãn nở vì nhiệt, nhà sản xuất chỉ đóng vào chai một lượng nước bằng \(90\% \) so với thể tích của chai nước. Đồng thời Viện y tế quốc gia Hoa Kỳ (NIH) khuyến nghị mỗi người nên uống đủ 2 lít nước mỗi ngày. Hỏi cần mua tối thiểu bao nhiêu chai nước suối của hãng A để đảm bảo theo khuyến nghị của NIH?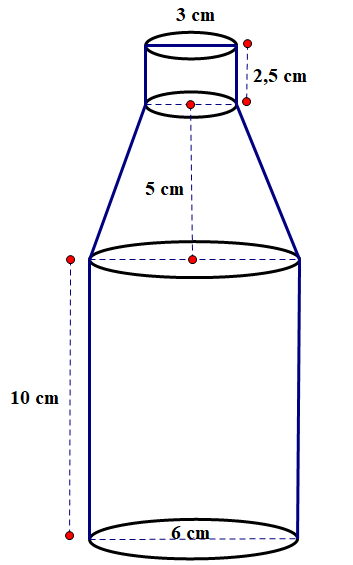

Một hộp kem hình trụ có đường kính 12 cm và chiều cao 15 cm đựng đầy kem. Kem sẽ được người bán hàng chia vào các bánh ốc quế hình nón có chiều cao 12 cm và đường kính 6 cm, có hình bán cầu trên đỉnh như hình vẽ.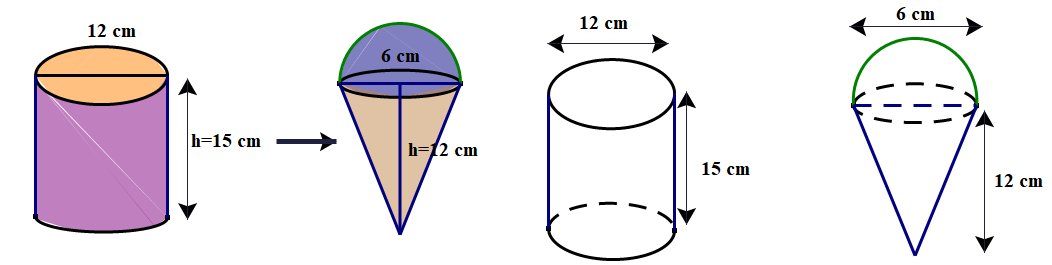a) Tính thể tích hộp kem hình trụ?
b) Tính số que kem có thể chia được? Biết rằng người bán hàng đã chia kem vào bánh ốc quế ít hơn \(5\% \) so với
thể tích thực của chiếc bánh như hình vẽ trên tính luôn phần bán cầu. Cho biết công thức tính thể tích:
Hình trụ là: \({\rm{V}} = {\rm{S}}\).h trong đó S là diện tích đáy hình trụ, h là chiều cao hình trụ
Hình nón: \({\rm{V}} = \frac{1}{3}\;{\rm{S}}\).h trong đó S là diện tích đáy hình nón, h là chiều cao hình nón
Hình cầu: \({\rm{V}} = \frac{4}{3}\pi {{\rm{R}}^3}\) trong đó \(\pi \approx 3,14;{\rm{R}}\) là bán kính hình cầu.

Hình bên miêu tả một chiếc bình đựng nước trong hai trường hợp: khi được đặt thẳng đứng và khi úp ngược lại. Biết phần gạch chéo trong hình là phần chứa nước và các số đo như trong hình vẽ. Biết rằng công thức tính thể tích hình trụ là \(V = \pi {R^2}.h\) với \(R\)là bán kính đáy và \(h\) là chiều cao hình trụ.
a) Hãy tính thể tích nước trong bình.
b) Hãy tính thể tích của bình?
(Các kết quả trong Câu làm tròn đến chữ số thập phân thứ nhất)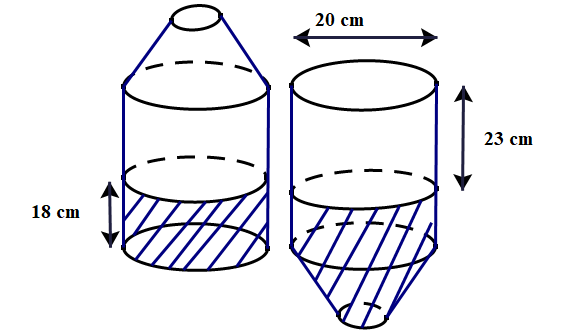

Một bình nước có dạng hình trự, phần lòng bên trong của bình nước cũng có dạng hình trụ có chiều cao là 20 cm và chu vi mặt đáy là \(10\pi cm\).
a) Tính thể tích nước có thể chứa trong bình khi đổ đầy. (Kết quả chính xác hai chữ số thập phân)
b) Hiện tại mực nước có trong bình cao 10 cm, một con quạ muốn uống nước trong bình thì cần phải thả vào bình những viên sỏi có thể tích tương đương một khối cầu đường kính là 4 cm. Hỏi con quạ phải thả tối thiểu vào trong bình bao nhiêu viên sỏi như nhau để có thể uống nước trong bình, biết tầm với của mỏ con quạ là 6 cm.

Một người nông dân gánh một quang gánh gồm 2 thúng gạo có kích thước và chứa lượng gạo hai bên như nhau. Một thúng gạo là nửa hình cầu có đường kính là 40 cm và để có thể đem được nhiều gạo hơn, người dân mới đổ đầy gạo vào thúng và vun gạo lên trên thành một hình nón có chiều cao 15 cm.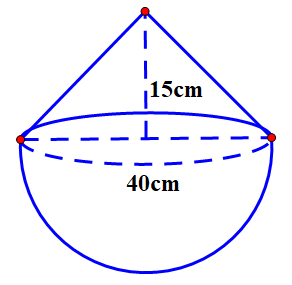

a) Tính lượng gạo trong 1 thúng của quang gánh (làm tròn đến chữ số thập phân thứ nhất)
b) Người nông dân dùng lon sữa bò có dạng hình trụu có bán kính đáy 4 cm, chiều cao bằng 10 cm để đong gạo vào thúng. Mỗi lần đong được lượng gạo bằng \(95\% \) thể tích lon. Hỏi người nông dân cần đong ít nhất bao nhiêu lon gạo để đủ gạo cho quang gánh như trên. Biết thể tích hình nón \(V = \frac{1}{3}.3,14.{R^2}.h\); thể tích hình cầu
\(V = \frac{4}{3}.3,14.{R^3}\); thể tích hình \[V = 3,14.{R^2}.h\].

Một tháp đồng hồ có phần dưới có dạng hình hộp chữ nhật, đáy là hình vuông có cạnh dài 5 m, chiều cao của hình hộp chữ nhật là 12 m. Phần trên của tháp có dạng hình chóp đều, các mặt bên là các tam giác cân chung đinh (hình vẽ). Mỗi cạnh bên của hình chóp dài 8 m.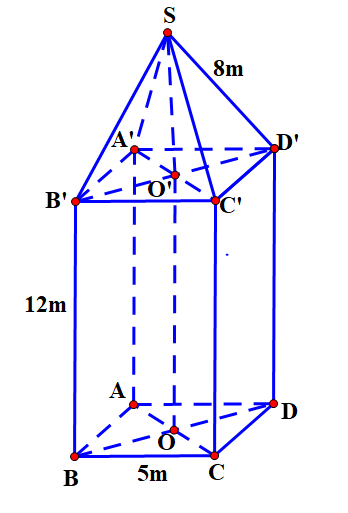a) Tính theo mét chiều cao của tháp đồng hồ? (làm tròn đến chữ số thập phân thứ nhất).
b) Cho biết thể tích của hình hộp chữ nhật được tính theo công thức \(V = S.h\), trong đó \(S\) là diện tích mặt đáy, \(h\) là chiều cao của hình hộp chữ nhật. Thể tích của hình chóp được tính theo công thức \(V = \frac{1}{3}\;S.h\), trong đó \(S\) là diện tích mặt đáy, \(h\) là chiều cao của hình chóp. Tính thể tích của tháp đồng hồ này? (Làm tròn đến hàng đơn vị).

Cho tháp nước như hình dưới đây, tháp được thiết kế gồm thân tháp có dạng khối trụ, phần mái phía trên có dạng khối nón và đáy là nửa khối cầu. Không gian bên trong toàn bộ tháp được minh hoạ theo hình vẽ với đường kính đáy hình trụ, hình cầu và của hình nón đều bằng 3 m, chiều cao hình trụ là 2 m, chiều cao hình nón là 1 m. Tính thể tích của toàn bộ không gian bên trong tháp nước.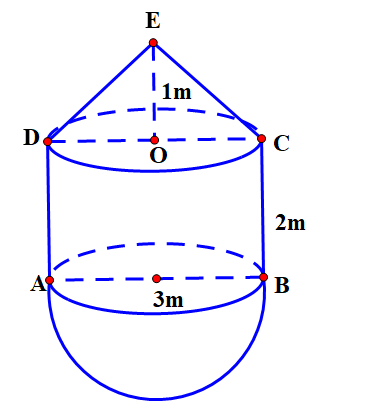

Đặt quả bóng vào trong một hộp hình lập phương sao cho quả bóng tiếp xúc với các mặt của hình lập phương đó. Hãy tính đường kính \(d\) của quả bóng, biết thể tích hình khối lập phương\(V\, = \,4096\;\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\)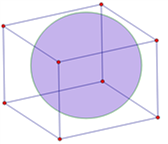

Một xe bồn chở nước sạch cho một khu chung cư có 200 hộ dân. Mỗi đầu của bồn chứa nước là 2 nửa hình cầu (có kích thước như hình vẽ). Bồn chứa đầy nước và lượng nước chia đều cho từng hộ dân. Tính xem mỗi hộ dân nhận được bao nhiêu lít nước sạch? (làm tròn đến chữ số thập phân thứ hai, lấy \(\pi = 3,14\)).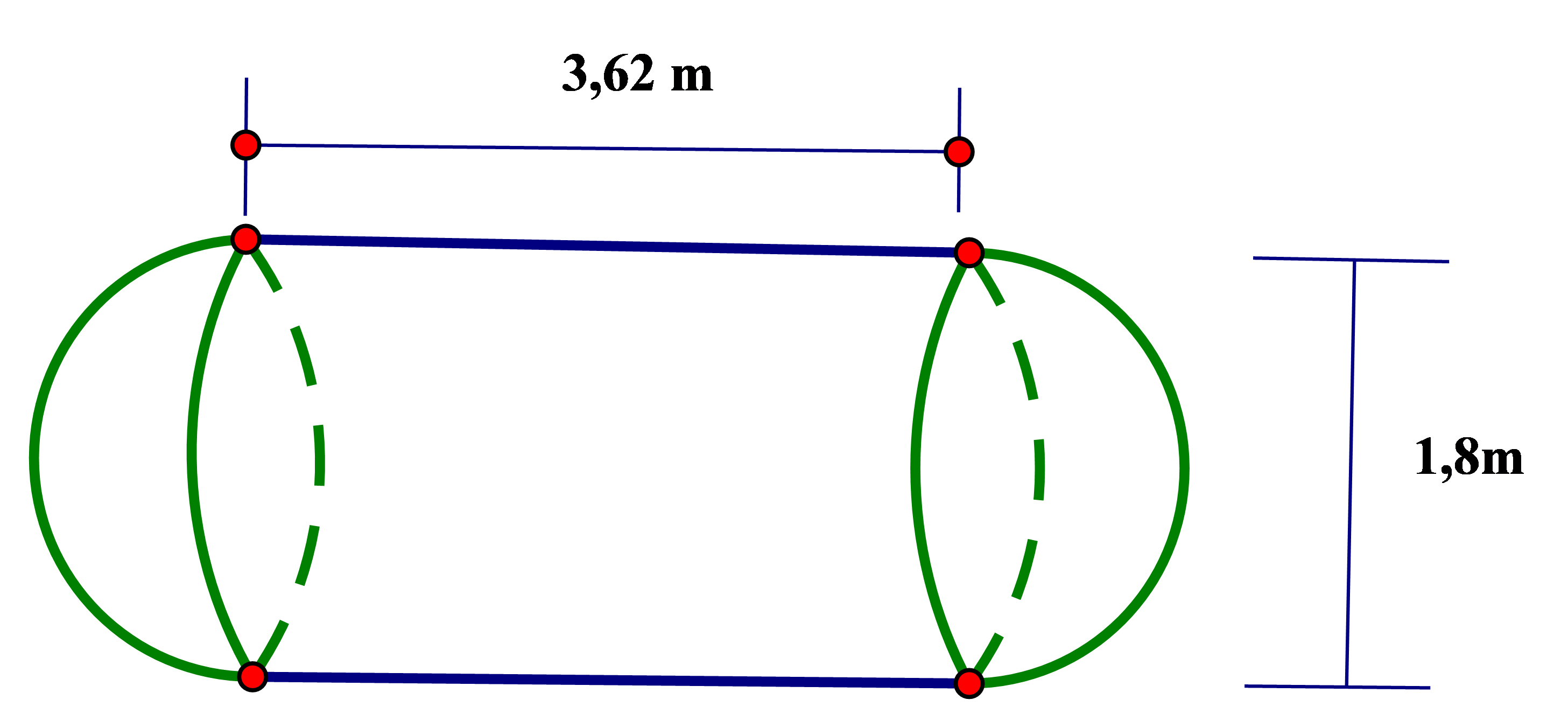

Một bình hình trụ có đường kính đáy 1dm, chiều cao 2dm bên trong có chứa viên bi hình cầu có bán kính 4cm. Hỏi phải đổ vào bình bao nhiêu lít nước để nước đầy bình (làm tròn đến chữ số thập phân thứ nhất).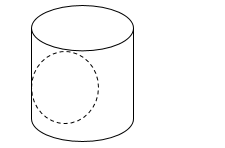

Cho biết: \(\)\({V_{Tru}} = \pi .{r^2}h\) với \(r\) là bán kính đáy; \(h\) là chiều cao hình trụ.
\({V_{{\rm{C\c{C}u}}}} = \frac{{\rm{4}}}{{\rm{3}}}\pi {R^3}\) với \(R\) là bán kính hình cầu

Một cái mũ bằng vải của nhà ảo thuật với kích thước như hình vẽ.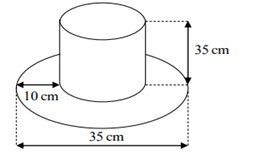

Hãy tính tổng diện tích vải cần để làm cái mũ đó biết rằng vành mũ hình tròn và ống mũ hình trụ (làm tròn đến hàng đơn vị).

Ở hai quầy hàng \[A\] và \[B\] trong hội hoa xuân, người ta bán hai loại bắp rang bơ lần lượt được đựng trong hai loại hộp hình nón và hình trụ với thông tin về giá cả và định lượng như trong hình dưới đây. Vỏ hộp được làm bằng giấy, phần này nhận được tài trợ của công ty giấy, nên cả hai quầy không tốn chi phí làm vỏ hộp. Hỏi bạn \[H\] nên mua bắp rang bơ ở quầy \[A\] hay quầy \[B\] để bạn có lợi hơn? Tại sao?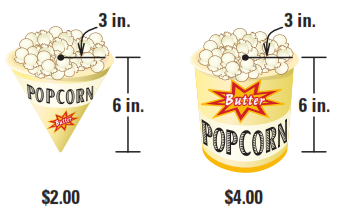

Bạn đang tìm kiếm 1 món đồ mà mọi người nhìn vào biết ngay bạn là một Ảo thuật gia thực sự? Đó là một chiếc nón bằng vải nỉ được may theo phong cách cao bồi. Chiếc mũ ảo thuật này chính là sản phẩm mà bất kỳ các nhà ảo thuật gia nào cũng đều đội khi biểu diễn. Ảo thuật gia gỡ chiếc nón xuống và bắt đầu tạo nên phép màu. Đầu tiên chiếc nón huyền bí bắn ra một loạt bông tuyết với một tiếng nổ lớn. Sau tiếng nổ là một ngọn lửa bốc cháy dữ dội từ bên trong chiếc mũ, và điều đặc biệt nhất chính là từ trong ngọn lửa, chú chim bồ câu xuất hiện một cách thật là thần kỳ. Không chỉ thế bạn còn có thể lấy ra thỏ, chim hoặc 1 số vật dụng bạn yêu thích. Đặc biệt chiếc mũ này còn là một đạo cụ thích hợp cho những ai diễn sân khấu.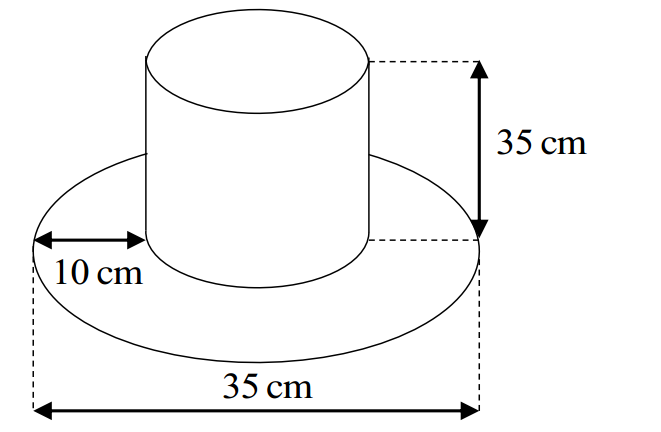Một chiếc mũ bằng vải của nhà ảo thuật với kích thước như hình vẽ. Hãy tính tổng diện tích vải cần để làm cái mũ đó. Biết rằng vành mũ hình tròn và ống mũ hình trụ.

Từ một khúc gỗ hình trụ cao \[15\,\,cm,\] người ta tiện thành một hình nón có đáy là hình tròn bằng với đáy hình trụ, chiều cao của hình nón bằng chiều cao của hình trụ. Biết phần gỗ bỏ đi có thể tích là \[3610\pi \] (cho biết \[\pi \approx 3,14\]). Công thức tính thể tích hình trụ: \[V{\rm{ }} = \pi {R^2}h,\] thể tích hình nón: \[V = \frac{1}{3}\pi {R^2}h\] (với \[R\] là bán kính đáy, \[h\] là chiều cao khúc gỗ). Tính thể tích khúc gỗ hình trụ, (làm tròn tới hàng đơn vị).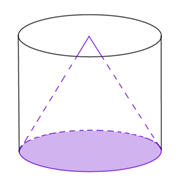

Một xô đựng nước có dạng hình nón cụt (như hình vẽ). Đáy xô có bán kính \({\rm{MN}} = 9\;{\rm{cm}}\), miệng xô là đáy lớn của hình nón cụt có \({\rm{BC}} = 21\;{\rm{cm}}\), chiều cao của xô là \({\rm{BN}} = {\rm{h}},{\rm{MC}} = 36\;{\rm{cm}}\). Biết \(\widehat {{\rm{ANM}}} = \widehat {{\rm{ABC}}} = {90^^\circ }\).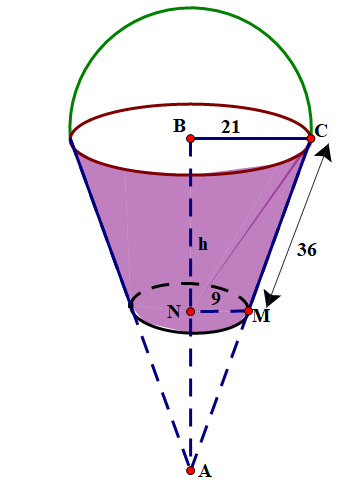a) Hỏi xô có thể chứa bao nhiêu lít nước? (Ghi kết quả làm tròn 1 chữ số thập phân). Biết công thức tính thể tích hình nón cụt là \({\rm{V}} = \frac{1}{3}\pi {\rm{h}}\left( {{\rm{r}}_1^2 + {\rm{r}}_2^2 + {{\rm{r}}_1}{{\rm{r}}_2}} \right)\) với h là chiều cao của hình nón cụt; \({{\rm{r}}_1},{{\rm{r}}_2}\) lần lượt là bán kính 2 đáy của hình nón cụt.
b) Bạn Nam dùng xô trên để lấy nước cho vào bể chứa hình hộp chữ nhật có kích thước \(120\;{\rm{cm}} \times 100\;{\rm{cm}} \times 90\;{\rm{cm}}\). Biết trong mỗi lần lấy nước cho vào bể chứa thì lượng nước hao hụt là \(20\% \). Hỏi bạn Nam cần lấy ít nhất bao nhiêu lần để đầy bể chứa? Bỏ qua thể tích thành bể.

Một bồn nước inox có dạng hình hộp chữ nhật có chiều dài \(1,5\,{\rm{m}}\), chiều rộng \(1,2\,{\rm{m}}\), chiều cao \(1,4\,{\rm{m}}\). Hỏi bồn nước đựng đầy được bao nhiêu mét khối nước? (Bỏ qua bề dày của bồn nước).

Một thùng hình hộp chữ nhật có chiều dài là \(0,5\,{\rm{m}}\); chiều rộng là \(0,4\,{\rm{m}}\); chiều cao là \(3\,{\rm{dm}}\). Hỏi cần phải mua bao nhiêu lít dầu để đổ đầy thùng?

Một trường THCS ở thành phố chuẩn bị xây dựng một hồ bơi cho học sinh với kích thước như sau: chiều rộng là \[6\] m, chiều dài \[12,5\] m, chiều sâu \[2\] m. Sức chứa trung bình \[0,5{\rm{ }}{{\rm{m}}^2}\]/ người (Tính theo diện tích mặt đáy). Thiết kế như hình vẽ sau
a) Hồ bơi có sức chứa tối đa bao nhiêu người?
b) Tính thể tích của hồ bơi? Lúc này người ta đổ vào trong đó lít nước. Tính khoảng cách của mực nước so với mặt hồ? (\[1{\rm{ }}{{\rm{m}}^3} = {\rm{ }}1000\]lít)

Hình lập phương có thể tích là \(125\;{{\rm{m}}^3}\).
a) Tính độ dài \(d\) là độ dài đường chéo một mặt của hình lập phương.
b) Tính độ dài \(D\) là độ dài đường chéo của hình lập phương.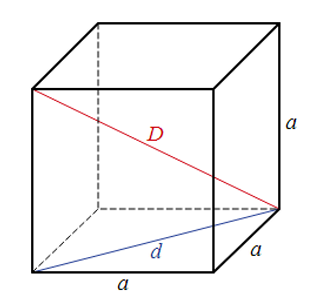

Một bình chứa nước hình hộp chữ nhật có diện tích đáy là \[20\,d{m^2}\] và chiều cao \[3\,dm\]3dm. Người ta rót hết nước trong bình ra những chai nhỏ mỗi chai có thể tích là \[0,35\,d{m^3}\]được tất cả 72 chai. Hỏi lượng nước có trong bình chiếm bao nhiêu phần trăm thể tích bình?

Một bể kính nuôi cá có dạng hình hộp chữ nhật có chiều dài \(100\)cm, chiều rộng \(50\)cm, chiều cao \(60\)cm. Mực nước trong bể cao bằng\(\frac{3}{4}\) chiều cao bể. Tính thể tích nước trong bể đó. (độ dày kính không đáng kể). Công thức tính thể tích nước trong bể là\(V = S.h\) với \(S\) là diện tích mặt đáy bể và \(h\) là chiều cao mực nước trong bể.

Một xe tải đông lạnh chở hàng có thùng xe dạng hình hộp chữ nhật với kích thước như hình bên. Bạn hãy tính giúp thể tích của thùng xe và diện tích phần Inox đóng thùng xe (tính luôn sàn).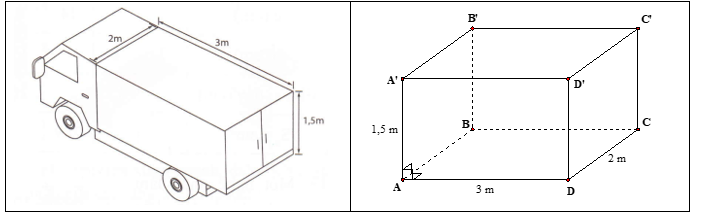

Một xe tải chở hàng có thùng xe dạng hình hộp chữ nhật với kích thước như hình bên.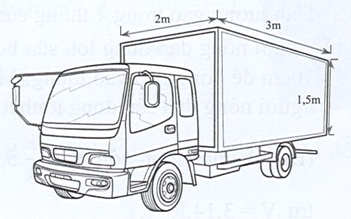

a) Hãy tính thể tích của thùng xe. (Độ dày của thùng xe xem như không đáng kể)
b) Người ta xếp vào thùng xe tải trên các thùng hàng loại A có dạng hình lập phương độ dài cạnh 40 cm để vận chuyển. Hỏi mỗi lần vận chuyển xe có thể chở được nhiều nhất bao nhiêu thùng hàng loại A?

Một vật chặn giấy bằng nhựa đặc có dạng hình lăng trụ đứng, hai đáy là các tam giác đều cạnh 60 mm, chiều cao lăng trụ là 150 mm.
a) Tính diện tích toàn phần khối lăng trụ.
b) Tính thể tích khối lăng trụ (làm tròn đến \({\rm{m}}{{\rm{m}}^3}\)), cho biết công thức tính diện tích tam giác đều là \({\rm{S}} = \frac{{{a^2}\sqrt 3 }}{4}\), trong đó \(a\) là độ dài cạnh tam giác đều.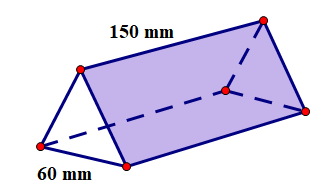

Một chiếc lều ở trại hè của học sinh có dạng hình chóp tứ giác đều: chiều cao \(SO\) là 2,8 mét và cạnh đáy hình vuông \(ABCD\) là 3 mét. \(SE\) là chiều cao đại diện cho một mặt bên.
a) Tính thể tích không khí trong chiếc lều.
b) Tính diện tích vải dùng may lều (không tính các phần mép may liên kết) biết lều này không có đáy. Biết thể tích hình chóp đều cho bởi công thức \({\rm{V}} = \frac{1}{3} \cdot \) S. \(h\); trong đó, \(S\) là diện tích đáy và \(h\) là chiều cao của hình chóp đều, kết quả làm tròn đến chữ số thập phân thứ nhất.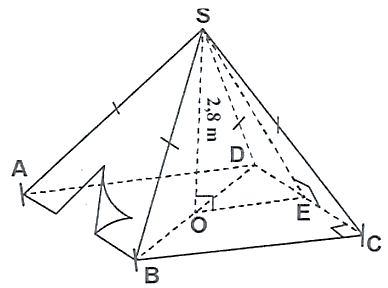

Bạn An làm một mô hình kim tự tháp để giới thiệu về lịch sử Ai Cập cổ đại. Vì kích thước của khu trưng bày, An quyết định làm mô hình kim tự tháp từ một tấm bìa hình vuông có cạnh là 5 dm. Nhờ sự giúp đỡ của thầy, An đã tạo một mô hình kim tự tháp bằng cách cắt bỏ bốn tam giác cân bằng nhau có đáy là cạnh của hình vuông rồi gấp lên sau đó ghép lại để thành một hình chóp tứ giác đều như hình vẽ. An đã cắt miếng bia trên sao cho cạnh đáy của khối chóp tứ giác đều là \(2\sqrt 2 dm\). Em hãy tính thể tích của khối chóp tứ giác đều đó (theo đơn vị\(d{m^3}\)), biết thể tích của hình chóp được tính theo công thức: \(V = \frac{1}{3}\;S.h\), trong đó \(S\) là diện tích mặt đáy, \(h\) là chiều cao hình chóp, các mặt bên của hình chóp tứ giác đều là các tam giác cân bằng nhau, \(CB \bot GH\) và \(A\) là tâm hình vuông.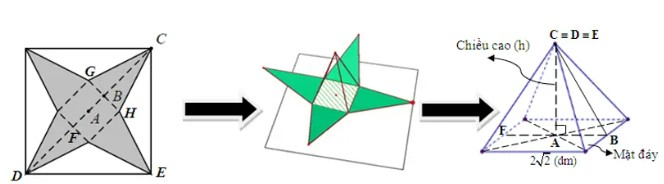

Người ta thiết kế chậu trồng cây có dạng hình chóp tam giác đều (như hình vẽ bên) biết cạnh đáy khoảng 20 cm, chiều cao khoảng 35 cm, độ dài trung đoạn khoảng 21 cm.
a) Người ta muốn sơn các bề mặt xung quanh chậu. Hỏi diện tích bề mặt cần sơn là bao nhiêu?
b) Tính thể tích của chậu trồng cây đó (làm tròn kết quả đến hàng phần trăm). Biết đường cao của mặt đáy hình chóp là 17 cm.

Một số khu vực vùng núi tỉnh Hà Giang nước ta vào mùa khô rất thiếu nước. Để có nước dùng các hộ dân ở đây đều xây dựng các hồ chứa nước mưa. Một hộ dân xây một hồ chứa nước mưa hình lập phương có thể tích là \(64\;{m^3}\).
a) Tính độ dài \(D\) là độ dài đường chéo của hình lập phương.
b) Nếu dùng 2 vòi nước cùng chảy vào bể thì mất bao nhiêu phút mới đầy bể? (làm tròn đến phút). Biết vòi 1 sau 2 giây chảy được 17 lít nước, vòi 2 sau 3 giây chảy được 35 lít nước.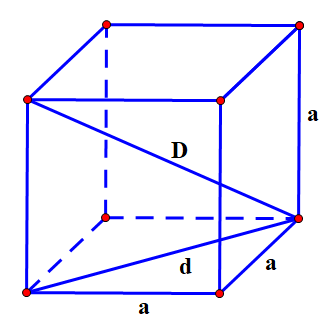

Để tạo một mô hình kim tự tháp (hình chóp tứ giác đều) từ tấm bìa, bạn Hạ cắt theo hình bên (ở giữa là hình vuông cạnh 4 dm, các tam giác bên ngoài là tam giác cân có chiều cao 3 dm) rồi gấp 4 tam giác lại chung đỉnh. Hãy tính thể tích của mô hình được tạo thành ở trên (làm tròn đến 1 chữ số thập phân)

Một cái lều ở trại hè có dạng lăng trụ đứng tam giác (với các kích thước trên hình: \[AH = 1,2\,m\]; \[BC = 3,2\,m\]; \[CC' = 5\,m\]).
a) Tính thể tích khoảng không ở bên trong lều.
b) Cần phải có ít nhất bao nhiêu m2 vải bạt để dựng lều đó?(Không tính các mép và nếp gấp của lều)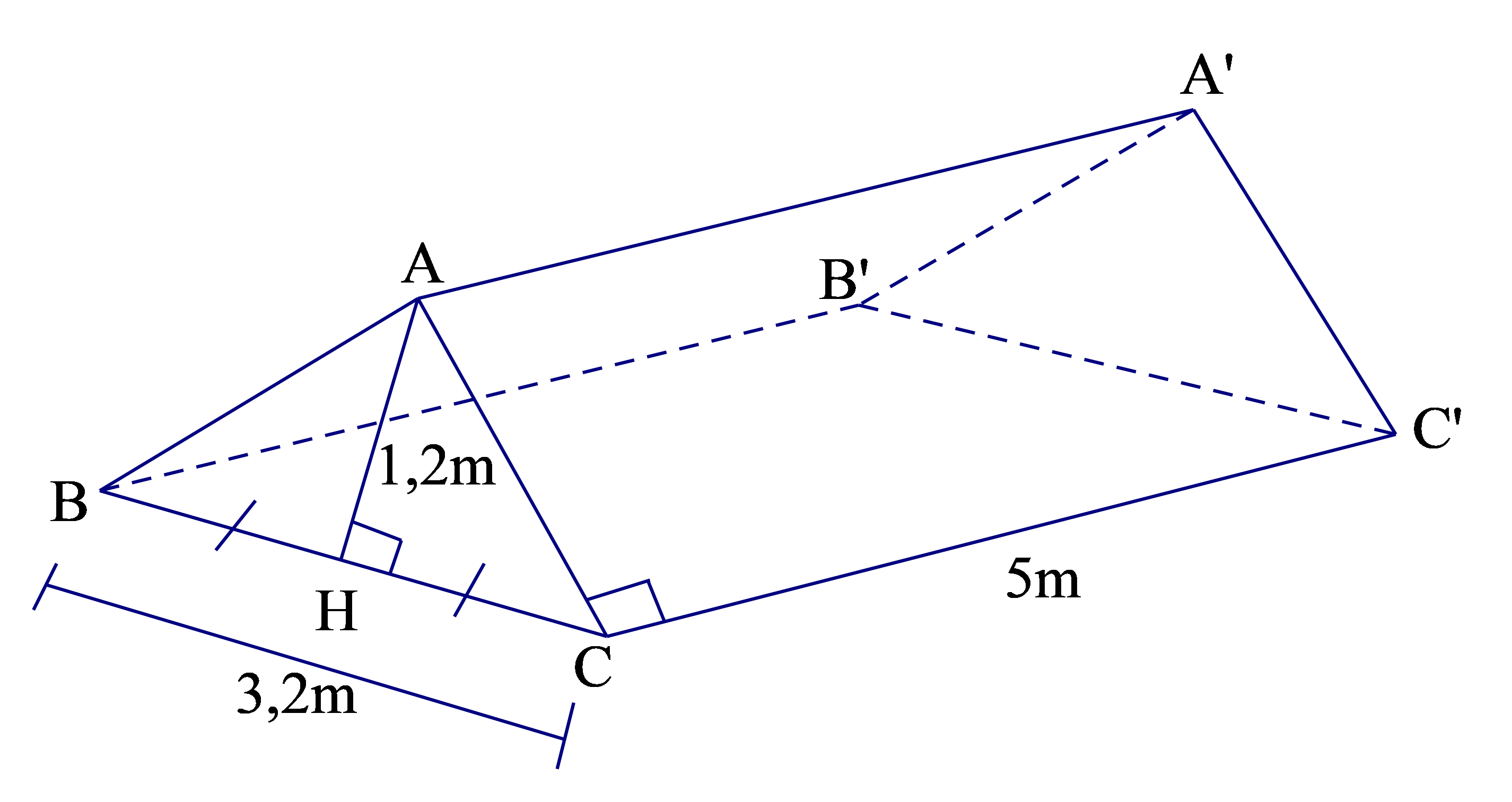

Một hồ bơi có dạng là một lăng trụ đứng tứ giác với đáy là hình thang vuông (mặt bên (1) của hồ bơi là 1 đáy của lăng trụ) và các kích thước như đã cho (xem hình 2). Biết rằng người ta dùng một máy bơm với lưu lượng là 42 m3/phút và sẽ bơm đầy hồ mất 25 phút. Tính chiều dài của hồ.