50 bài tập Một số yếu tố xác suất có lời giải
50 câu hỏi
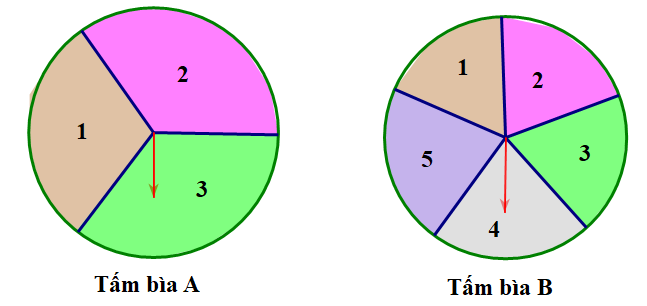
Tấm bìa cứng A hình tròn được chia thành 3 hình quạt có diện tích bằng nhau, đánh số 1; 2; 3 và tấm bìa cứng B hình tròn được chia thành 5 hình quạt có diện tích bằng nhau, đánh số 1; 2; 3; 4; 5 (xem hình vẽ). Trục quay của A và B được gắn mũi tên ở tâm. Bạn Bình quay tấm bìa A, bạn An quay tấm bìa B. Quan sát xem mũi tên dừng ở hình quạt nào trên hai tấm bìa.
a) Mô tả không gian mẫu của phép thử.
b) Tính xác suất của các biến cố sau:
T: “ Tích hai số ở hình quạt mà hai mũi tên chỉ vào bằng 6”;
M: “Tích hai số ở hình quạt mà hai mũi tên chỉ vào nhỏ hơn 5”
L: “Tích hai số ở hình quạt mà hai mũi tên chỉ vào là số chẵn”.
Một dĩa tròn bằng bìa cứng được chia thành 12 phần bằng nhau và ghi các số từ \(1,2,3, \ldots ,12\). Chiếc kim được gắn cố định vào trục quay ở tâm của dĩa. Xét phép thử “quay dĩa tròn 1 lần”.
a) Liệt kê các kết quả thuận lợi cho biến cố A: “Chiếc kim chi vào hình quạt ghi số chia hết cho 3”.
b) Tính xác suất của biến cố A .
Tổ 1 của lớp 9 A có 12 học sinh, trong đó có 8 học sinh thích môn Toán và 7 học sinh thích môn Văn. Tính xác suất chọn ra 1 em học sinh bất kỳ vừa thích môn Văn, vừa thích môn Toán.
Lớp 9 A có 2 bạn nam hát hay là Khôi và Thiên; 2 bạn nữ hát hay là Phương và Dung. Cô chủ nhiệm lớp muốn chọn ra 2 bạn để hát song ca trong lễ bế giảng năm học.
a) Hãy liệt kê các cách chọn ngẫu nhiên 2 bạn để hát song ca.
b) Tính xác suất của mỗi biến cố sau:
A: “Trong 2 bạn được chọn có 1 bạn nam và một bạn nữ”
B: “Trong 2 bạn được chọn, có bạn Phương”
Tỉ lệ học sinh bị cận thị ở một trường trung học cơ sở là \(16\% \). Gặp ngẫu nhiên một học sinh, xác suất học sinh đó không bị cận thị là bao nhiêu?
Bạn An đến một hội chợ được tổ chức gần nhà trong dịp tết Nguyên Đán. Bạn tham gia trò chơi ném bi. Đích đến là một bảng có 25 ô như hình vẽ.
5 | 3 | 3 | 3 | 5 |
3 | \( - 2\) | \( - 1\) | \( - 2\) | 3 |
3 | \( - 1\) | 5 | \( - 1\) | 3 |
3 | \( - 2\) | \( - 1\) | \( - 2\) | 3 |
5 | 3 | 3 | 3 | 5 |
Cách tính điểm như sau:
* Ném ra ngoài bảng trừ 5 điểm.
* Ném vào một trong 25 ô điểm tính được ghi như hình bên.
* Nếu sau 10 lần ném mà:
- Đạt 50 điểm thì nhận được phần quà trị giá 500000 đồng.
- Đạt từ 30 điểm đến 49 điểm thì nhận được phần quà trị giá 300000 đồng.
- Đạt từ 15 điểm đến 29 điểm thì nhận được phần quà trị giá 50000 đồng.
- Dưới 15 điểm không có quà.
a) Trong 9 lần ném bi, bạn An ném được 5 lần vào ô điểm 5, một lần ra ngoài bảng, 2 lần vào ô điểm 3, một lần ô điểm -1 . Tính số điểm bạn An nhận được sau 9 lần ném.
b) Hỏi bạn An có cơ hội nhận phần quà trị giá 300000 không? Nếu có thì bạn An phải ném vào ô nào? Tính xác suất để bạn An nhận được phần quà đó.
Một hộp có 25 thẻ cùng loại , mỗi thẻ được ghi một trong các số \(1;2;3;4;5; \ldots \ldots ;25\); hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố sau:
a) “Số xuất hiện trên thẻ được rút ra là số chia hết cho 5”;
b) “Số xuất hiện trên thẻ được rút ra là số có hai chữ số”;
c) “Số xuất hiện trên thẻ được rút ra là số có hai chữ số và tổng các chữ số bằng 5”;
An gieo hai con xúc xắc cân đối và đồng chất.
a) Hãy xác định không gian mẫu của phép thử trên.
b) Tính xác suất của biến cố “Tổng số chấm trên hai con xúc xắc bằng 8”.
Một túi chứa 3 viên bi màu xanh và một số viên bi màu đỏ có cùng kích thước và khối lượng. Bạn An lấy ra ngẫu nhiên một viên bi. Biết rằng xác suất lấy ra viên bi màu xanh là 0,6. Hỏi trong túi có bao nhiêu viên bi màu đỏ?
Một hộp chứa 5 quả bóng màu đỏ và một số quả bóng màu trắng. Các quả bóng có khối lượng và kích thước như nhau. Lấy ngẫu nhiên một quả bóng từ hộp, xem màu rồi trả lại hộp. Biết xác suất biến cố: “Lấy ra được 1 quả bóng màu trắng” có xác suất là 0,75. Tính số quả bóng màu trắng có trong hộp.
Gieo một đồng tiền cân đối đồng chất liên tiếp cho đến khi lần đầu tiên xuất hiện mặt ngửa hoặc cả 6 lần xuất hiện mặt sấp thì dừng lại.
a) Mô tả tập A các kết quả có thể xảy ra của sự kiện.
b) Tính xác suất (khả năng xảy ra) của sự kiện:
A: “Số lần gieo không vượt quá ba”
B: “Số lần gieo là năm”
C: “Số lần gieo là sáu”
Một lớp gồm 50 học sinh trong đó có
- 30 học sinh giỏi tiếng Anh,
- 25 học sinh giỏi tiếng Pháp,
- 15 học sinh giỏi tiếng Trung,
- 12 học sinh giỏi tiếng Anh và tiếng Pháp,
- 7 học sinh giỏi tiếng Anh và tiếng Trung,
- 5 học sinh giỏi tiếng Pháp và tiếng Trung,
- 2 học sinh giỏi cả ba thứ tiếng trên.
Chọn ngẫu nhiên một học sinh trong lớp để kiểm tra năng lực ngoại ngữ của bạn ấy. Gọi \(A\) là biến cố chọn được học sinh chỉ giỏi tiếng Anh, \(n(A)\) là số học sinh chỉ giỏi tiếng Anh có trong lớp, xác suất (khả năng) xảy ra của biến cố \(A\) gọi là \(P(A)\) với \(P(A) = \frac{{n(A)}}{{50}}\). Tính \(P(A)\).
Mặt xuất hiện | 3 chấm | 5 chấm | 2 chấm | 6 chấm |
Số lần gieo | 14 | 12 | 16 | 8 |
Hãy tính xác suất của các biến cố:
a) A: “Gieo được mặt 5 chấm”.
b) B: “Gieo được mặt có số chấm chẵn”.
Một hộp chứa 10 thẻ được đánh số từ 1 đến 10, người ta rút ngẫu nhiên hai thẻ khác nhau. Tính xác suất để rút được hai thẻ mà tích hai số được đánh trên thẻ là số lẻ.
Gieo ngẫu nhiên 1 đồng tiền đồng chất và cân đối 2 lần. Tính xác suất của các biến cố sau:
- A: “Mặt ngửa xuất hiện đúng 1 lần”
- B: “Mặt ngửa xuất hiện ít nhất 1 lần”
- C: “Mặt ngửa xuất hiện 2 lần”
Bạn Cáo rủ bạn Cừu tham ra một trò chơi như sau: Cáo có một chiếc hộp trong đó có 100 mẩu giấy ghi các số có hai chữ số (từ 00 đến 99). Cáo lấy ra ngẫu nhiên một số bất kì, sau đó Cừu đoán một lần. Nếu Cừu đoán đúng sẽ được 70 nghìn đồng, còn nếu Cừu đoán sai chỉ mất một nghìn đồng. Theo bạn thì Cừu có nên chơi không? Vì sao?
Một lớp gồm 50 học sinh trong đó có 30 học sinh giỏi tiếng Anh, 25 học sinh giỏi tiếng Pháp, 15 học sinh giỏi tiếng Trung, 12 học sinh giỏi tiếng Anh và tiếng Pháp, 7 học sinh giổ tiếng Anh và tiếng Trung, 5 học sinh giỏi tiếng Pháp và tiếng Trung, 2 học sinh giỏi cả ba thứ tiếng trên. Chọn ngẫu nhiên một học sinh trong lớp để kiểm tra. Tính xác suất để:
a) Học sinh đó chỉ giỏ̉i tiếng Anh.
b) Học sinh đó giỏi hai trong ba ngoại ngữ trên.
Xúc xắc hay còn gọi là xí ngầu là một khối nhỏ hình lập phương được đánh dấu chấm tròn với số lượng từ một đến sáu cho cả sáu mặt. Hai viên xúc xắc hình lập phương được làm bằng gỗ có tổng diện tích toàn phần là \(23,52\;{\rm{c}}{{\rm{m}}^2}\).
a) Tính khối lượng của hai viên xúc xắc? Cho biết: khối lượng \(m = V.{\rm{ }}D\) , trong đó \(V\) là thể tích và khối lượng riêng của gỗ là \(D = 0,8gam/c{m^3}\).
b) Người ta gieo hai viên xúc xắc trên cùng một lần. Hỏi xác suất để xuất hiện hai mặt giống nhau là bao nhiêu phần trăm? Kết quả làm tròn đến chữ số thập phân thứ nhất.
Một cái hộp đựng 6 viên bi đỏ và 4 viên bi xanh. Lấy lần lượt 2 viên bi từ cái hộp đó. Tính xác suất để viên bi được lấy lần thứ 2 là bi xanh.
Việt làm một bài kiểm tra trắc nghiệm lựa chọn 4 đáp án gồm 10 câu. Mỗi câu trắc nghiệm chỉ có 1 đáp án đúng. Trong 10 câu trắc nghiệm có 6 câu trong đề cương nên Việt thấy quen thuộc và chọn đúng đáp án. Những câu còn lại Việt chọn ngẫu nhiên vì không biết đáp án. Tính xác suất để Việt được 8 điểm.
Bạn An tung một đồng xu cân đối và đồng chất 2 lần, tính xác suất của biến cố A: “tung được lần thứ nhất là mặt sấp”.
Lấy ngẫu nhiên một thẻ từ một hộp chứa 20 thẻ được đánh số từ 1 đến 20. Tìm xác suất để thẻ được lấy ghi số lẻ và chia hết cho 3.
Trong trò chơi bánh xe quay số. Bánh xe số có 20 nấc điểm: \(5;10;15;20; \ldots ;100\)với các vạch chia đều nhau và giả sử rằng khả năng chuyển từ nấc điểm đã có tới các nấc điểm còn lại là như nhau. Trong mỗi lượt chơi có hai người tham gia, mỗi người được quay một lần và điểm của người chơi là điểm quay được. Người nào có số điểm cao hơn sẽ thắng cuôc, hòa nhau sẽ chơi lại lượt khác. Nam và Bình cùng tham gia một lượt chơi. Nam chơi trước và được 80 điểm. Hãy tính xác suất thực nghiệm của sự kiện Bình thắng cuộc ở lượt chơi này.
Một hộp đựng 1 viên bi đỏ, 1 viên bi xanh, 2 viên bi vàng có cùng kích thước và khối lượng, bạn Nam lấy ra một cách ngẫu nhiên 2 viên bi từ hộp.
a) Có bao nhiêu kết quả có thể xảy ra?
b) Tính xác suất của các biến cố sau:
A: “Hai viên bi lấy ra cùng màu”
B: “Hai viên bi lấy ra có 1 viên màu đỏ”
C: “Hai viên bi lấy ra khác màu”
Một hộp chứa 5 quả bóng màu đỏ và một quả bóng màu trắng. Các quả bóng có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên một quả bóng từ hộp xem màu rồi trả lại hộp. Biết xác suất của biến cố lấy được “Quả bóng màu đỏ” là 0,25. Hỏi trong hộp có bao nhiêu quả bóng màu trắng.
Gieo hai con xúc xắc cân đối và đồng chất. Tính xác suất để tổng số chấm xuất hiện ở mặt trên cùng của hai con xúc xắc bằng 10.
Hộp thứ nhất đựng 1 quả bóng trắng, 1 quả bóng đỏ. Hộp thứ 2 đựng 1 quả bóng đỏ, 1 quả bóng vàng. Lấy ra ngẫu nhiên từ mỗi hộp 1 quả bóng.
a) Xác định số phần tử của không gian mẫu ?
b) Biết rằng các quả bóng có cùng kích thước và cùng khối lượng. Hãy tính xác suất của biến cố A: “Có đúng một quả bóng màu đỏ trong 2 quả bóng lấy ra”.
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số nguyên dương không vượt quá 5 , hai thẻ khác nhau thì ghi hai số khác nhau. Lấy ngẫu nhiên một chiếc thẻ từ trong hộp, ghi lại số của thẻ lấy ra và bỏ lại thẻ đó vào hộp.
a) Sau 40 lần lấy thẻ liên tiếp, hãy tính xác suất thực nghiệm của các biến cố sau “Thẻ lấy ra ghi số chẵn” và “Thẻ lấy ra ghi số lẻ”.
b) Tính xác suất của các biến cố “Thẻ lấy ra ghi số chã̃n” và “Thẻ lấy ra ghi số lẻ”.
Gieo 1 con xúc xắc đồng chất 2 lần. Tính xác suất tổng số chấm xuất hiện bằng 6.
Gieo ngẫu nhiên một con xúc xắc cân đối và đồng chất. Tính xác suất của biến cố: Xuất hiện mặt có số dấu chấm không lớn hơn 3.
Một hộp có 10 thẻ tròn với kích thước và khối lượng như nhau. Bạn An viết lên các thẻ đó tên 4 loại trái cây là: Táo, Hồng, Lê, Nho và tên 6 loài động vật là: Trâu, Bò, Gà, Vịt, Dê, Cừu, hai thẻ khác nhau thì viết hai tên khác nhau. Lấy ngẫu nhiên một thẻ trong hộp.
a) Viết tập hợp \(E\) gồm các kết quả có thể xảy ra đối với tên sinh vật được viết trên viên bi lấy ra.
b) Viết tập hợp gồm các kết quả có thể xảy ra đối với biến cố G: “Trên thẻ lấy ra viết tên một loài động vật”. Mỗi phần tử của tập hợp đó gọi là một kết quả thuận lợi cho biến cố G.
c) Tìm tỉ số của số các kết quả thuận lợi cho biến cố G và số phần tử của tập hợp \(E\).
Trong hộp có một số bút xanh, một số bút vàng và một số bút đỏ. Lấy ngẫu nhiên 1 bút từ hộp, xem màu gì rồi trả lại. Lặp lại hoạt động trên 40 lần ta được kết quả như sau:
Màu bút | Xanh | Vàng | Đỏ |
Số lần | 14 | 10 | 16 |
Tính xác suất của biến cố không lấy ra được bút màu vàng?
Một hộp có 25 thẻ cùng loại , mỗi thẻ được ghi một trong các số \(1;2;3;4;5; \ldots ..25\); hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố sau :
a) “Số xuất hiện trên thẻ được rút ra là số chia hết cho 5”;
b) “Số xuất hiện trên thẻ được rút ra là số có hai chữ số”;
c) “Số xuất hiện trên thẻ được rút ra là số có hai chữ số và tổng các chữ số bằng 5”;
Lớp 9A có 38 học sinh, trong đó có 18 nữ. Có 6 bạn nữ tham gia câu lạc bộ thể thao và 8 bạn nam không tham gia câu lạc bộ thể thao. Chọn ngẫu nhiên một học sinh trong lớp. Tính xác suất để học sinh đó là một bạn nam có tham gia câu lạc bộ thể thao.
Một hộp có 20 thẻ cùng loại, mỗi thẻ được ghi một trong các số \(1;2;3;4;5; \ldots ..;20\); hai thẻ (1đ) khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố sau:
a) “Số xuất hiện trên thẻ được rút ra là số có chữ số tận cùng là 2”.
b) “Số xuất hiện trên thẻ được rút ra là số có một chữ số”.
c) “Số xuất hiện trên thẻ được rút ra là số có hai chữ số với tích các chữ số bằng 4”.
Để chuẩn bị cho ngày Hội xuân được tổ chức hằng năm, khối 9 chịu trách nhiệm tổ chức một số gian hàng và trò chơi. Khối 9 của trường có 16 lớp nên ban tổ chức chuẩn bị 16 phiếu để các lớp bốc thăm. Các phiếu được đánh số thứ tự từ 1 đến 16 và trên đó có ghi một trong ba nhiệm vụ “tổ chức gian hàng ẩm thực”, “tổ chức gian hàng quà lưu niệm”, “tổ chức trò chơi dân gian”. Biết rằng trường dự định tổ chức 7 gian “ẩm thực” và số gian “trò chơi dân gian” nhiều gấp hai lần số gian “quà lưu niệm”. Lớp 9A1 được mời lên bốc thăm đầu tiên. Tính xác suất để lớp 9 A 1 bốc được phiếu “tổ chức trò chơi dân gian”.
Để hòa chung với không khí World Cup, ở một thành phố tổ chức giải bóng đá lứa tuổi THCS bao gồm 32 đội tham gia chia thành 8 bảng. Ở vòng bảng, 2 dội có thứ hạng cao nhất sẽ được đi tiếp vào vòng trong (vòng loại trực tiếp). Thắng được 3 điểm, hòa được 1 điểm, thua 0 điểm. Nếu hai đội cùng điểm sẽ so hiệu số bàn thắng - thua. Ở bảng A , đội D của bạn An nằm trong bảng hạt giống sau 2 lượt đấu số hạng như sau:
+ Đội \({\rm{A}}:4\) điểm + Đội \({\rm{B}}:2\) điểm \(\quad + \) Đội \({\rm{C}}:2\) điểm \(\quad \) + Đội \({\rm{D}}:1\) điểm
Ở lượt đấu diễn ra song song 2 trận \(A - C\) và \(B - D\). Các em hãy tính xác suất vào vòng trong của đội D biết rằng đội D luôn có hiệu số bàn thắng thấp nhất?
Xác suất = (số khả năng vào vòng trong): (số khả năng xảy ra). \(100\% \)
Gieo ngẫu nhiên một con xúc xắc cân đối và đồng chất hai lần.
a) Hãy mô tả không gian mẫu.
b) Xác định các biến cố sau :
A: “Tổng số chấm xuất hiện trong hai lần gieo không bé hơn 10”;
B: “Mặt 5 chấm xuất hiện ít nhất một lần”.
c) Tính \(P(A),P(B)\).
Bạn Nam có 3 chiếc ảnh giấy. Nam tung lần lượt từng chiếc ảnh lên để rơi trên bàn. Tính xác suất để sau 3 lần tung thì 3 chiếc ảnh có 2 chiếc sấp, 1 chiếc ngửa.
Xuân bỏ một số viên bi xanh và đỏ kích thước và khối lượng giống nhau vào túi. Mỗi lần lấy ra ngẫu nhiên một viên bi, xem màu của nó rồi trả lại túi. Lặp lại phép thử đó 100 lần, Xuân thấy có 40 lần mình lấy được bi đỏ. Biết rằng trong túi có 9 bi xanh, hãy ước lượng xem trong túi có bao nhiêu viên bi đỏ.
Tính xác suất của biến cố sau đây:
a) A: “Tổng số chấm trên hai mặt xuất hiện của hai quân xúc xắc \( \le 6\)”
b) B: “Có đúng một quân xúc xắc xuất hiện số chấm là số lẻ”
c) C: “Số chấm xuất hiện trên hai quân xúc xắc hơn kém nhau 2”
Gieo ngẫu nhiên xúc xắc 6 mặt cân đối một lần. Xét các biến cố sau:
A: “Số chấm xuất hiện trên con xúc xắc là số lẻ và chia hết cho 3”.
B: “Số chấm xuất hiện trên con xúc xắc là số lớn hơn 2”.
C: “Số chấm xuất hiện trên con xúc xắc là số tròn trăm”.
D: “Số chấm xuất hiện trên con xúc xắc là số chia cho 4 dư 1”.
a) Trong các biến cố trên, hãy chỉ ra biến cố nào là biến cố chắc chắn, biến cố nào là biến cố không thể.
b) Tính xác suất của biến cố ngẫu nhiên có trong các biến cố \(A,B,C,D\).
Để chuẩn bị cho buổi thi đua văn nghệ nhân ngày Nhà giáo Việt Nam 20/11, cô giáo đã chọn ra 10 học sinh gồm: 4 học sinh nữ là Hoa; Mai; Linh; Mi, 6 học sinh nam là Cuờng; Hung; Mỹ; Kiên ; Phúc; Hoàng. Chọn ngẫu nhiên một học sinh trong nhóm 10 học sinh tập múa trên.
a) Tìm số phần tử của tập hợp \(M\) gồm các kết quả xảy ra đối với tên học sinh được chọn ra.
b) Tính xác suất của mỗi biến cố sau :
- “Học sinh được chọn ra là học sinh nam”
- “Học sinh được chọn ra là học sinh nữ”
- “Học sinh được chọn ra là học sinh nam có tên bắt đầu bằng chữ \(H\)”
- “Học sinh được chọn ra là học sinh nũ có tên bắt đầu bằng chữ \(M\)”
Cho tập hợp \(K = \left\{ {1;6;2;7;3;9;0} \right\}\).
a) Có thể viết được bao nhiêu số có ba chữ số khác nhau từ các số trong tập hợp \(K\)?
b) Xác suất để số viết được là một số chẵn?
Một hộp chứa 4 tấm thẻ cùng loại được đánh số 1; 4; 7; 9. Bạn Khuê và bạn Hương lần lượt mỗi người lấy ra 1 tấm thẻ từ hộp. Tính xác suất của mỗi biến cố sau:
A: “Tích các số ghi trên 2 tấm thẻ là số lẻ”;
B: “Tổng các số ghi trên 2 tấm thẻ là số lẻ”;
C: “Số ghi trên tấm thẻ của bạn Khuê nhỏ hơn số ghi trên tấm thẻ của bạn Hương”.
Gieo hai con xúc xắc cân đối và đồng chất. Xét hai biến cố sau:
A: “Xuất hiện hai mặt có cùng số chấm”;
B: “Tổng số chấm trên hai con xúc xắc lớn hơn 8”.
Biến cố nào có khả năng xảy ra cao hơn?
Gieo đồng thời hai con xúc xắc cân đối, đồng chất I và II. Tính xác suất của các biến cố sau:
E: “Có đúng 1 con xúc xắc xuất hiện mặt 6 chấm”
F: “Có ít nhất một con xúc xắc xuất hiện mặt 6 chấm”
G: “Tích của hai số chấm xuất hiện trên hai con xúc xắc nhỏ hơn hoặc bằng 6”
Có hai túi đựng các tấm thẻ. Túi I đựng 4 tấm thẻ ghi các chữ cái TT, TH, HT và HH. Túi II đựng 2 tấm thẻ ghi các chữ cái T và H.
Từ mỗi túi rút ngẫu nhiên ra một tấm thẻ rồi ghép hai thẻ lại với nhau để được ba chữ cái, trong đó thẻ hai chữ cái đặt trước, chẳng hạn tấm thẻ TT ghép với tấm thẻ H được ba chữ cái TTH. Tính xác suất của các biến cố sau:
a) E: “Trong ba chữ cái, có hai chữ H và một chữ T”
b) F: “Trong ba chữ cái, có nhiều nhất hai chữ T”
Mỗi nhân viên của một công ty làm biệc ở một trong năm bộ phận của công ty đó là: Hành chính – Nhân sự; Truyền thông – Quảng cáo; Kinh doanh; Sản xuất; Dịch vụ.
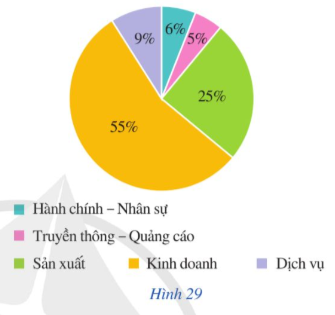
Biểu đồ hình quạt tròn trong Hình 29 thống kê tỉ lệ nhân viên thuộc mỗi bộ phận.
Chọn ngẫu nhiên một nhân viên của công ty. Tính xác suất của mỗi biến cố sau:
A: “Nhân viên được chọn thuộc bộ phận Kinh doanh”;
B: “Nhân viên được chọn không thuộc bộ phân Hành chính – Nhân sự hay Dịch vụ”.
Biểu đồ cột kép ở Hình 30 biểu diễn số lượng học sinh tham gia giải thi đấu thể thao của một trường trung học cơ sơ.
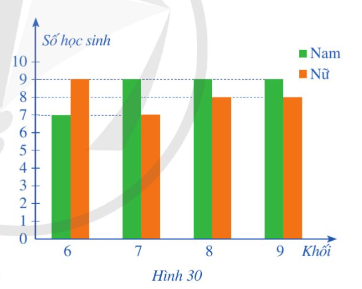
Chọn ngẫu nhiên một học sinh tham gia giải thi đấu thể thao của trường đó. Tính xác suất của mỗi biến cố sau:
A: “Học sinh được chọn là nam”;
B: “Học sinh được chọn thuộc khối 6”;
C: “Học sinh được là nữ và không thuộc khối 9”.








