Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án ( Đề 1)
21 câu hỏi
Điểm nào dưới đây thuộc đồ thị hàm số \(y = 2x - 4\)?
\(M\left( {0; - 4} \right).\)
\(N\left( {0;4} \right).\)
\(P\left( {4;0} \right).\)
\(Q\left( { - 4;0} \right).\)
Cho mặt phẳng tọa độ \(Oxy\) như hình vẽ dưới đây.
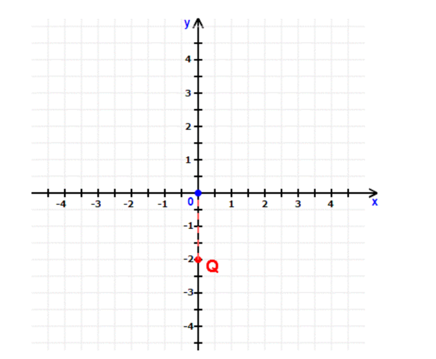
Tọa độ của điểm \(Q\) là
\(Q\left( {0; - 2} \right).\)
\(Q\left( { - 2;0} \right).\)
\(Q\left( {2;0} \right).\)
\(Q\left( {0;2} \right).\)
Cho đường thẳng \(y = ax + b\). Với giá trị \(a\) thỏa mãn điều kiện nào sau đây thì góc tạo bởi đường thẳng đo với trục \(Ox\) là góc nhọn?
\(a > 0.\)
\(a < 0.\)
\(a = 0.\)
\(a \ne 0.\)
Một xe ô tô chạy với vận tốc \(60{\rm{ km/h}}\). Hàm số biểu thị quãng đường \(S\left( t \right)\)\(\left( {{\rm{km}}} \right)\) mà ô tô đi được trong thời gian \(t{\rm{ }}\left( {\rm{h}} \right)\) là
\(S\left( t \right) = 60t.\)
\(S\left( t \right) = 60 + t.\)
\(S\left( t \right) = 60 - t.\)
\(S\left( t \right) = \frac{{60}}{t}.\)
Trong các phương trình sau, phương trình nào không phải là phương trình bậc nhất một ẩn?
\(0x + 2 = 0\).
\(2x + 1 = 0\).
\( - 2x = 0.\)
\(\frac{x}{2} + 3 = 0\).
Phương trình \(\frac{{2x}}{3} + \frac{1}{2} = 0\) có hạng tử tự do là:
\(\frac{2}{3}\).
\(\frac{1}{3}.\)
\(2\).
\(\frac{1}{2}\).
Chọn câu sai trong các câu sau:
Gọi số học sinh trong một lớp là \(x\) (học sinh) thì điều kiện cần là \(x \in {\mathbb{N}^*}.\)
Gọi thời gian làm bài tập của một học sinh là \(x\) (giờ) thì điều kiện cần là \(x > 0.\)
Gọi số sản phẩm của một công nhân làm được trong một ngày là \(x\) thì điều kiện cần là \(x < 0.\)
Gọi số tuổi của một công nhân làm trong một ngày là \(x\) thì điều kiện cần là \(x > 0.\)
Bạn An vào siêu thị mua bút và vở hết \(25\) nghìn đồng. Nếu gọi \(x\) là số tiền để mua vở thì số thiền mua bút (nghìn đồng) là
\(25 - x.\)
\(25 + x.\)
\(\frac{{25}}{x}.\)
\(25x.\)
Cho hình vẽ dưới đây:
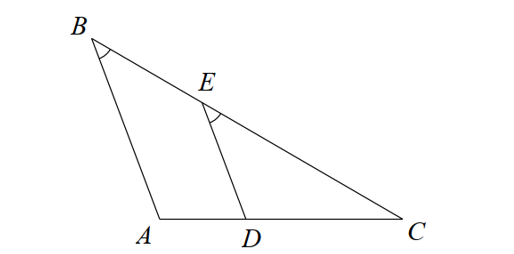
Hệ thức theo Định lí Thalès của hình trên là
\(\frac{{CE}}{{CB}} = \frac{{CD}}{{CA}}\).
\(\frac{{BE}}{{CB}} = \frac{{CA}}{{AD}}\).
\(\frac{{CE}}{{BE}} = \frac{{AD}}{{CD}}\).
\(\frac{{DE}}{{AB}} = \frac{{AC}}{{AD}}\).
Cho hình vẽ dưới đây:
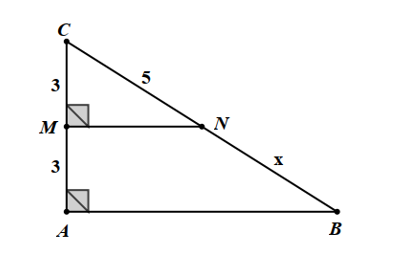
Độ dài \(x\) là
\(5.\)
\(3.\)
\(10.\)
\(6.\)
Cho các hình vẽ:
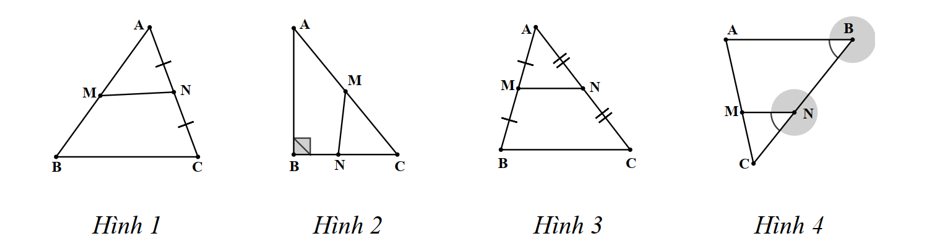
Đoạn thẳng \(MN\) là đường trung bình của tam giác \(ABC\) trong hình vẽ nào?
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Cho tam giác \(ABC\), \(AD\) là đường phân giác của \(\widehat {BAC}\)\(\left( {D \in BC} \right)\). Tỉ lệ thức nào sau đây đúng?
\(\frac{{AB}}{{BD}} = \frac{{AC}}{{BC}}.\)
\(\frac{{AD}}{{AC}} = \frac{{BD}}{{DC}}.\)
\(\frac{{DB}}{{AB}} = \frac{{DC}}{{AC}}\).
\(\frac{{DB}}{{DC}} = \frac{{BC}}{{AC}}\).
Năm nay tuổi bố gấp \(10\) lần tuổi Minh. Bố Minh tính rằng sau 24 năm nữa thì tuổi bố chỉ gấp \(2\) lần tuổi Minh. Gọi tuổi của Minh hiện nay là \(x\)\(\left( {x \in \mathbb{N}} \right)\).
a) Sau 24 năm nữa tuổi của Minh là \(x + 24\) (tuổi).
b) Sau 24 năm nữa tuổi của bố Minh là \(10x + 24\) (tuổi).
c) Sau 24 năm nữa thì tuổi bố chỉ gấp \(2\) lần tuổi Minh nên phương trình mô tả bài toán là:
\(10x + 24 = 2x + 24\).
d) Tuổi của bố Minh hiện tại là \(30\) tuổi.
Cho \(\Delta ABC\) có \(AD\) là trung tuyến, trọng tâm \(G\), đường thẳng đi qua \(G\) cắt các cạnh \(AB,\)\(AC\) lần lượt tại \(E,F\). Từ \(B,C\) kẻ các đường song song với \(EF\) cắt \(AD\) lần lượt tại \(M,N\).
a) \(\frac{{BE}}{{AE}} = \frac{{MG}}{{AG}}\).
b) \(\frac{{DN}}{{MD}} = \frac{{DB}}{{DC}}\).
c) \(\frac{{BE}}{{AE}} + \frac{{CF}}{{AF}} = 1\).
d) \(\frac{{AB}}{{AE}} + \frac{{CA}}{{AF}} = 3\).
Cho hàm số \(y = f\left( x \right) = \frac{{x - 3}}{{ - x + 1}}\). Tính giá trị của biểu thức \(A = f\left( { - 1} \right) + f\left( { - 3} \right) - 2f\left( 0 \right).\)
Cho hai đường thẳng \(y = 4x + m + 2\) và \(y = - 2x - 6 - 3m\) với \(m\) là tham số. Tìm giá trị của \(m\) để hai đồ thị của hàm số trên cắt nhau tại một điểm của trục tung.
Cho phương trình \(\left( {{m^2} - 3m + 2} \right)x = m - 2\) với \(m\) là tham số. Hỏi giá trị của \(m\) bằng bao nhiêu để phương trình có vô số nghiệm?
Tìm độ dài của \(x\) trong mỗi trường hợp sau: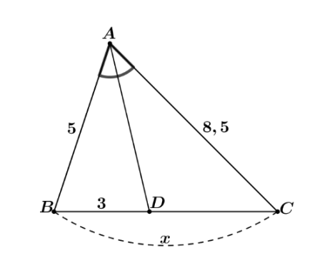
Cho hai đường thẳng \(\left( {{d_1}} \right):y = 2x - 1\) và \(\left( {{d_2}} \right):y = - x + 2\).
a) Chứng tỏ rằng hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cắt nhau. Xác định tọa độ giao điểm \(I\) của chúng và vẽ hai đường thẳng này trên cùng một hệ trục tọa độ.
b) Lập phương trình đường thẳng \(\left( {{d_3}} \right)\) đi qua \(I\) và song song với đường thẳng \(y = \frac{1}{2}x + 9.\)
Cho tam giác \(ABC\) vuông tại \(A\), biết \(AB = 21{\rm{ cm,}}\)\(AC = 28{\rm{ cm}}\), phân giác \(AD\) với \(D \in BC\).
a) Tính độ dài \(BC,BD,DC\).
b) Gọi \(E\) là hình chiếu của \(D\) trên \(AC\). Tính độ dài \(DE\) và \(EC\).
C) Gọi \(I\) là giao điểm của đường phân giác và \(G\) là trọng tâm tam giác \(ABC\). Chứng minh rằng \(IG\parallel AC.\)
Giải phương trình sau: \(\frac{{x + 1}}{{15}} + \frac{{x + 2}}{{14}} = \frac{{x + 3}}{{13}} + \frac{{x + 4}}{{12}}.\)