30 câu hỏi
Cho hàm số \[y = f(x)\] xác định trên \[\mathbb{R}\] và có đạo hàm \[y' = f'(x) = (x - 1){(x - 4)^2}{(5 - x)^3}.g(x)\], hàm số \[y = g(x)\] có đồ thị như hình vẽ. Hàm số \[y = f(x)\] có bao nhiêu điểm cực trị?
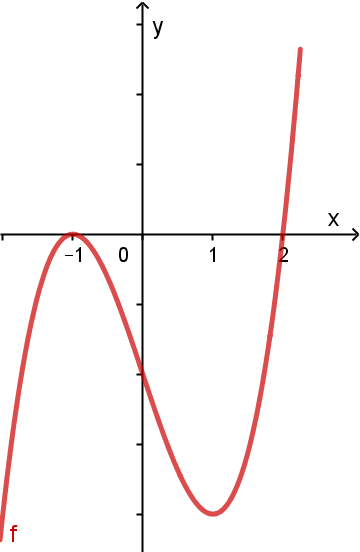
\(5\).
\(4\).
\(3\).
\(2\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
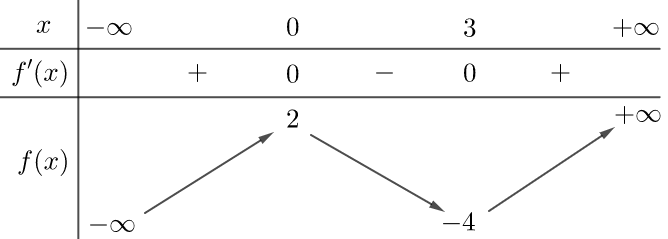
Giá trị cực tiểu của hàm số đã cho bằng
\(2\).
\(3\).
\(0\).
\( - 4\).
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau
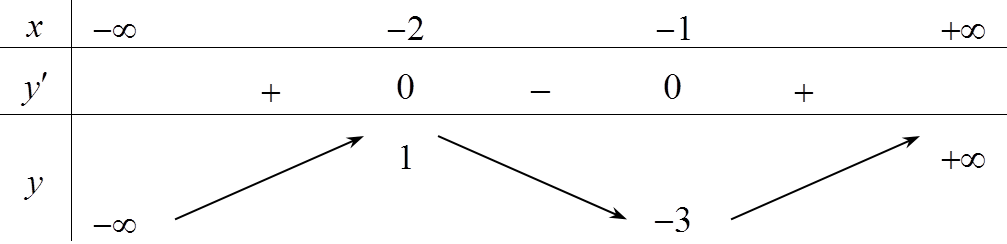
Hàm số đạt cực đại tại điểm
\[x = - 3\].
\[x = - 1\].
\[x = 1\].
\[x = - 2\].
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
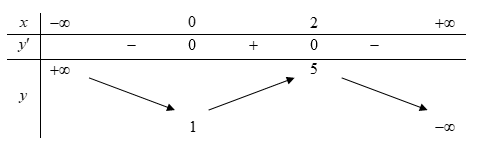
Hàm số đạt cực đại tại điểm
\(x = 1\)
\(x = 0\)
\(x = 5\)
\(x = 2\)
Hàm số \(y = f\left( x \right)\)có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
\( - 2\).
1.
0.
\( - 3\).
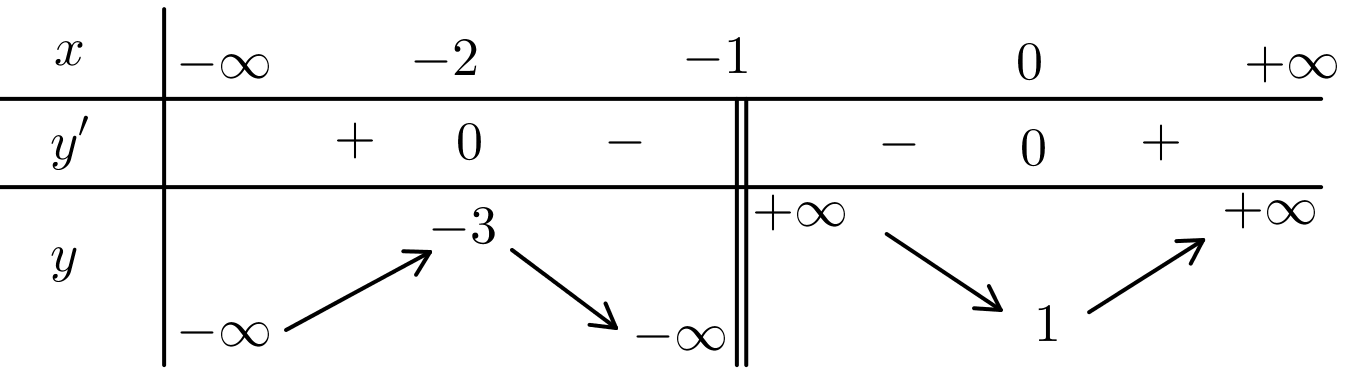
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
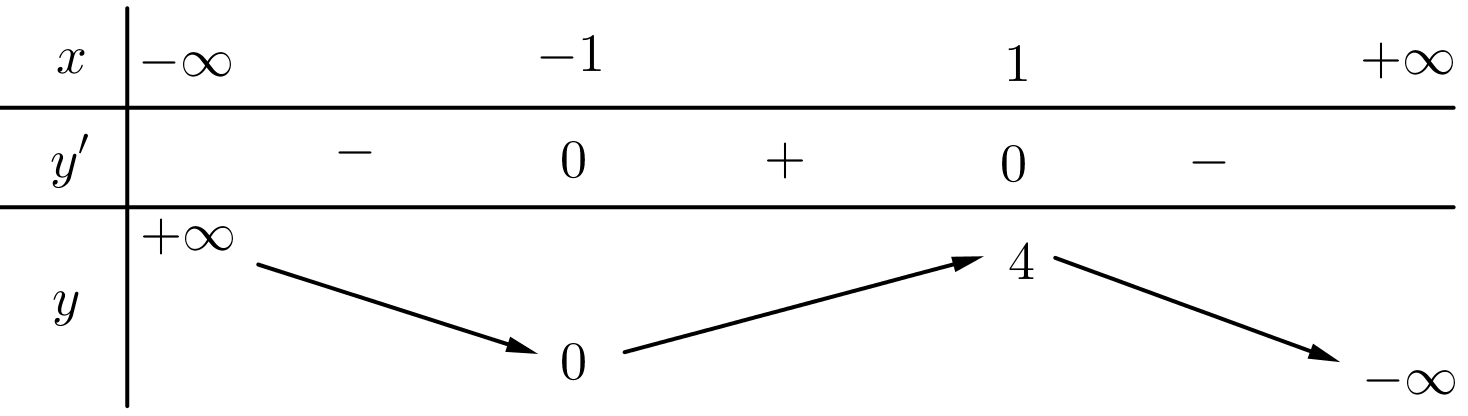
Giá trị cực đại của hàm số đã cho bằng
\( - 1\).
\(0\).
\(1\).
\(4\).
Cho hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\), bảng xét dấu của \(f'\left( x \right)\) như sau

Hàm số \(f\left( x \right)\) có bao nhiêu điểm cực trị?
3.
2.
1.
4.
Cho hàm số  , bảng xét dấu của
, bảng xét dấu của  như sau:
như sau:
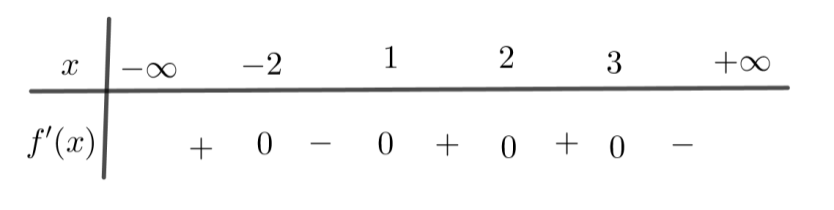
Số điểm cực đại của hàm số đã cho là
A. 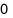 .
.
B. 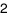 .
.
C. 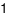 .
.
D.  .
.
Cho hàm số \(y = f\left( x \right)\)có bảng biến thiên như hình vẽ. Khẳng định nào sau đây là đúng?
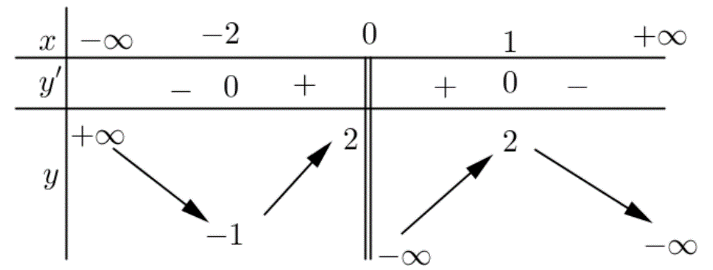
Hàm số không có giá trị cực tiểu.
Hàm số đạt cực đại tại \(x = 2\).
Giá trị cực đại của hàm số bằng \(1\).
Hàm số đạt cực tiểu tại \(x = - 2\).
Cho hàm số \(y = f\left( x \right)\)có bảng biến thiên sau
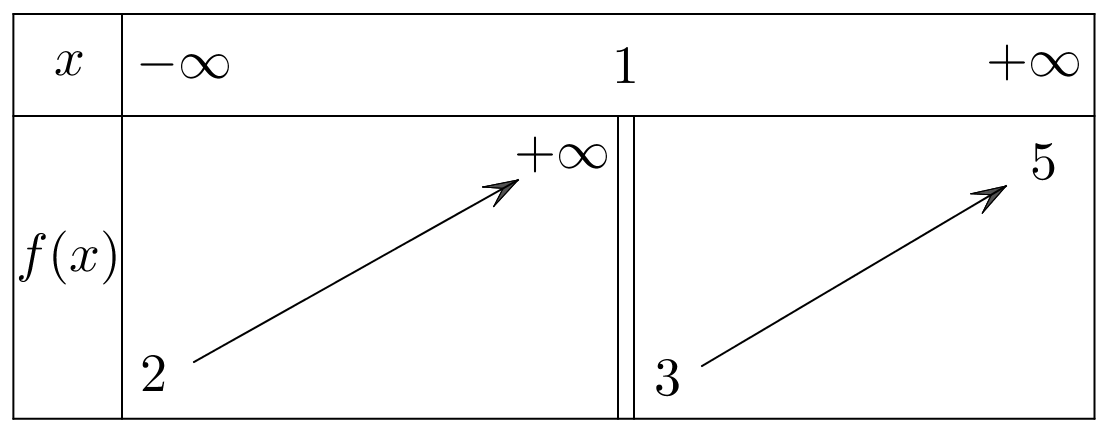
Hàm số đã cho có bao nhiêu điểm cực trị ?
\(1\).
\(2\).
\(3\).
\(0\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ bên. Khẳng định nào sau đây là đúng?
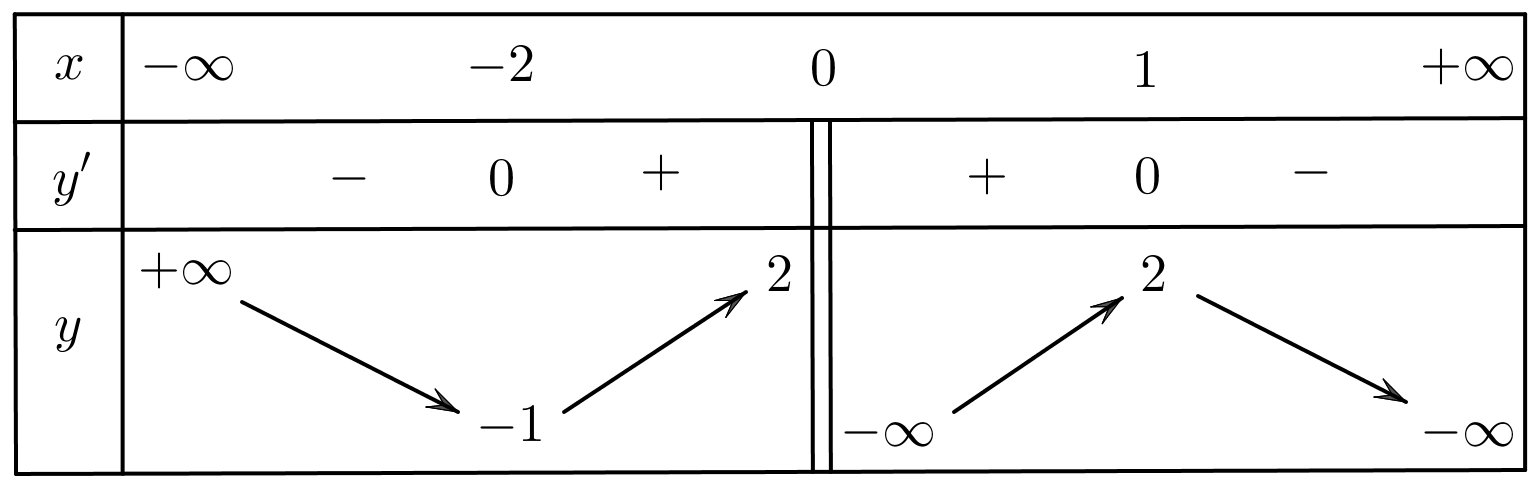
Hàm số \(f\left( x \right)\) đạt cực đại tại \(x = 2\).
Hàm số \(f\left( x \right)\) đạt cực tiểu tại \(x = - 1\).
Hàm số \(f\left( x \right)\) đạt cực tiểu tại \(x = - 2\).
Hàm số \(f\left( x \right)\) đạt cực đại tại \(x = - 2\).
Cho hàm số \(y = f(x)\) có bảng biến thiên như sau:
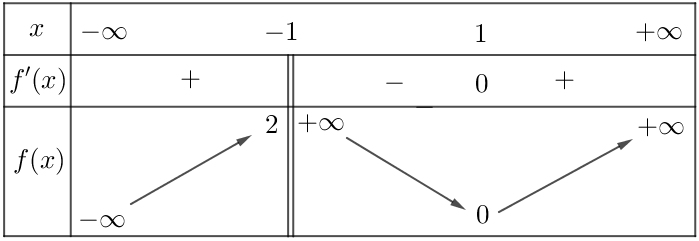
Khẳng định nào sau đây là đúng?
Giá trị cực đại của hàm số \(y = f(x)\) bằng 2.
Hàm số \(y = f(x)\) đạt cực tiểu tại \(x = 1\).
Hàm số \(y = f(x)\) đạt cực đại tại \(x = - 1.\).
Giá trị cực tiểu của hàm số \(y = f(x)\) bằng 1.
Cho hàm số \[f\left( x \right)\], bảng xét dấu của \[f'\left( x \right)\] như sau:

Số điểm cực trị của hàm số đã cho là
1.
3.
2.
4.
Cho hàm số \(f\left( x \right)\), bảng xét dấu \(f'\left( x \right)\) như sau:
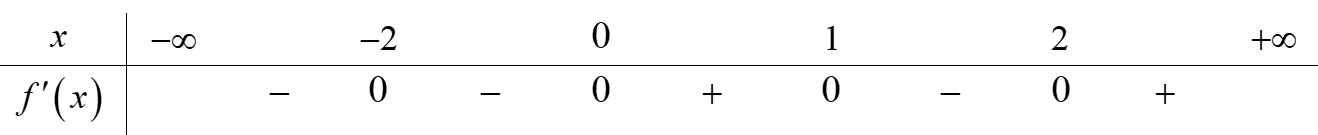
Số điểm cực tiểu của hàm số \(f\left( x \right)\)là
\(1\).
\(2\).
\(3\).
\(4\).
Cho hàm số \(f\left( x \right)\)có bảng xét dấu của \(f'\left( x \right)\)như sau:
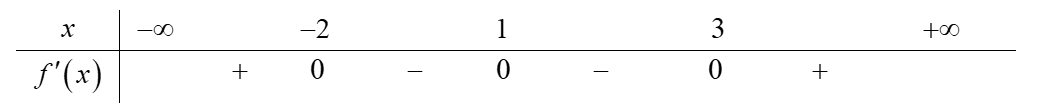
Số điểm cực trị của hàm số đã cho là
3.
0.
2.
1.
Cho hàm số \[y = f\left( x \right)\] có tập xác định \[D = \mathbb{R}\backslash \left\{ 0 \right\}\] và bảng xét dấu đạo hàm như sau

Số điểm cực trị của hàm số đã cho là
\(2\).
\(1\).
\(3\).
\(4\).
Cho hàm số \[f\left( x \right)\] liên tục trên \(\mathbb{R}\), bảng xét dấu của \(f'\left( x \right)\) như sau:
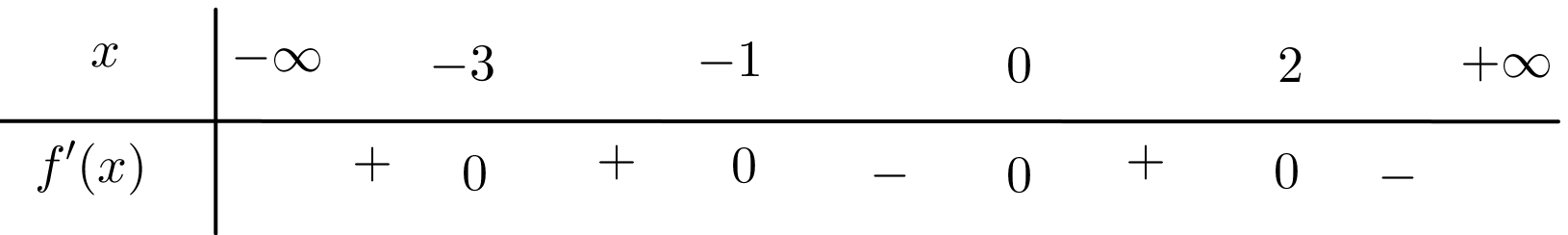
Tổng hoành độ các điểm cực đại của hàm số bằng
\[1\].
\[2\].
\[3\].
\[ - 2\].
Cho hàm số \[f\left( x \right)\] liên tục trên \(\mathbb{R}\), bảng xét dấu của \(f'\left( x \right)\) như sau:
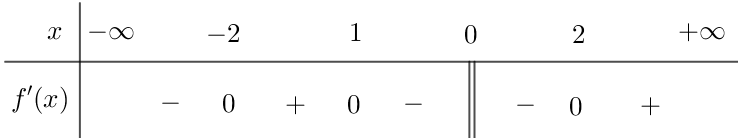
Hàm số có bao nhiêu điểm cực tiểu
\[1\].
\[2\].
\[3\].
\[4\].
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau:
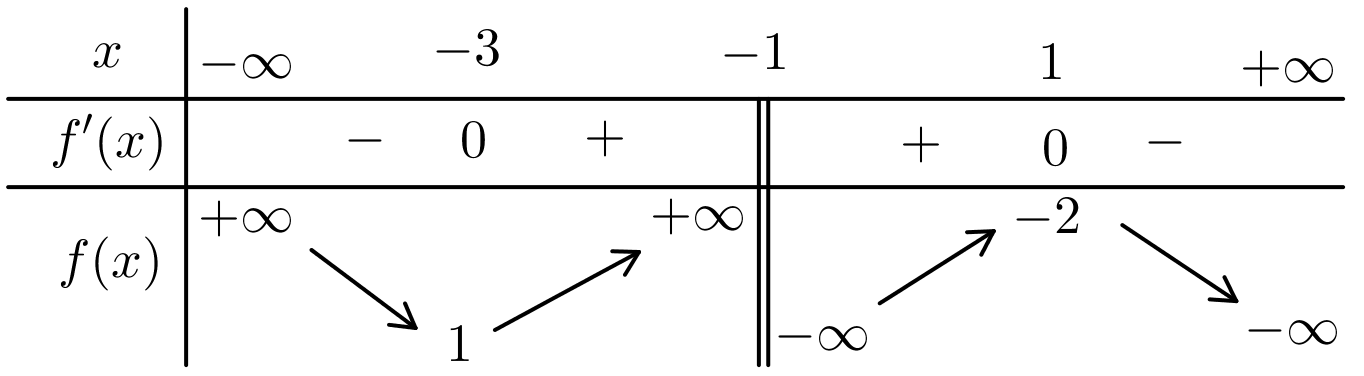
Giá trị cực đại của hàm số đã cho bằng
1.
\[ - 2\].
\[ - 3\].
\[ - 1\].
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu của đạo hàm như hình vẽ. Số điểm cực tiểu của hàm số đã cho là
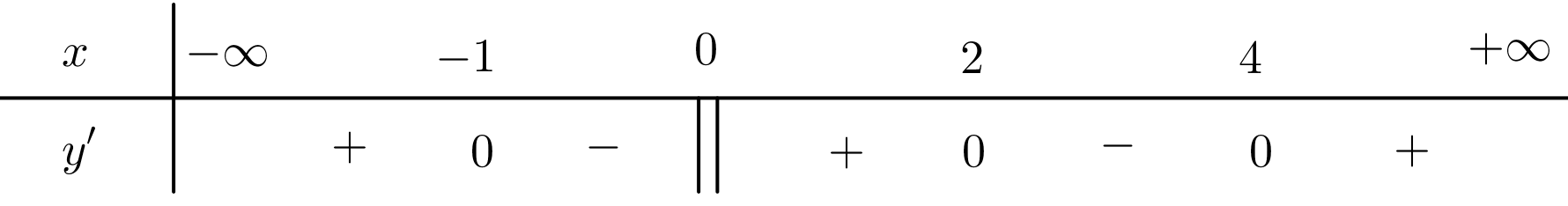
1.
3.
2.
4.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
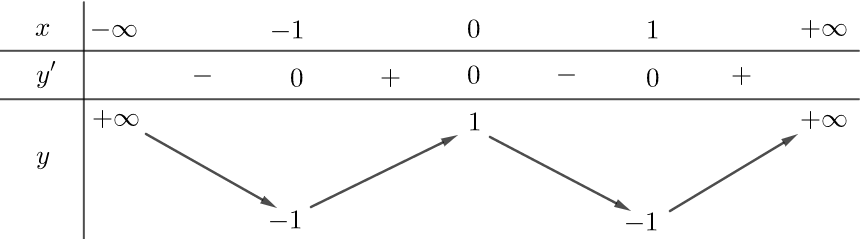
Số điểm cực trị của hàm số \(f\left( { - 2x} \right)\) là
\(5\).
\(3\).
\(6\).
\(4\).
Cho hàm số \(y = f\left( x \right)\)liên tục trên \[\mathbb{R}\] và có bảng xét dấu của \(f'\left( x \right)\)như sau:
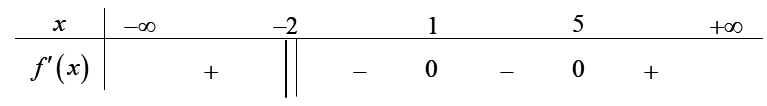
Tìm số cực trị của hàm số \(y = f\left( x \right)\).
3.
0.
2.
1.
Cho hàm số \(f\left( x \right)\)xác định trên \(\mathbb{R}\), bảng xét dấu của \(f'\left( x \right)\)như sau
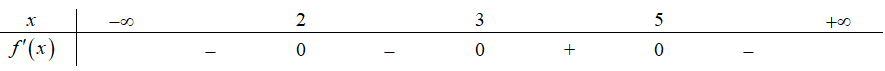
Hàm số \(f\left( x \right)\)có bao nhiêu điểm cực trị
3.
2.
1.
4.
Hàm số \(y = f\left( x \right)\)liên tục trên \(\mathbb{R}\)và có bảng xét dấu đạo hàm như sau. Hỏi hàm số \(y = f\left( x \right)\)có bao nhiêu điểm cực trị?

\(1\).
\(4\)
\(3\).
\(2\).
Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\)có bảng biến thiên như sau:
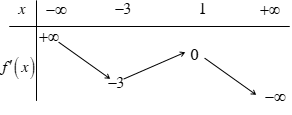
Số điểm cực trị của hàm số đã cho là:
\(3\).
\(0\).
\(2\).
\(1\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên:
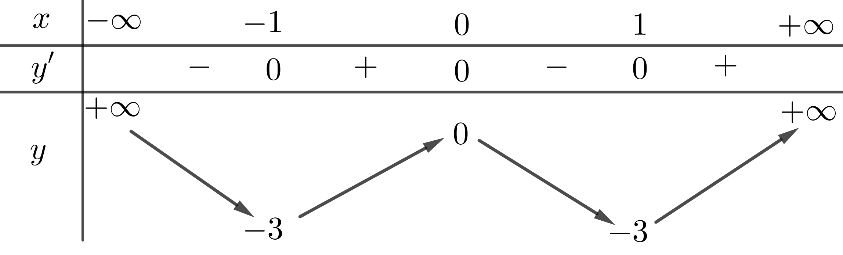
Hàm số \(g\left( x \right) = f\left( {2x - 1} \right)\) đạt cực đại tại
\(x = 0\).
\(x = \frac{1}{2}\).
\(x = 1\).
\(x = - 1\).
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = x\left( {x - 1} \right),\forall x \in \mathbb{R}\). Số điểm cực trị của hàm số đã cho là
\(2\).
\(0\).
\(3\).
\(1\).
Cho hàm số \[f\left( x \right)\] có đạo hàm \[f'\left( x \right) = {\left( {x + 1} \right)^2}{\left( {x + 2} \right)^3}\left( {2x - 3} \right)\]. Tìm số cực trị của hàm số \[f\left( x \right)\].
\(3\).
\(2\).
\(1\).
\(0\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {x^2}\left( {{x^2} - 4} \right)\), \(x \in \mathbb{R}\). Mệnh đề nào sau đây là đúng?
Hàm số đã cho có \(2\) điểm cực trị.
Hàm số đã cho đạt cực đại tại \(x = 2\).
Hàm số đã cho có \(3\) điểm cực trị.
Hàm số đã cho đạt cực tiểu tại \(x = - 2\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {x + 1} \right){\left( {x - 2} \right)^2}{\left( {x + 3} \right)^3}{\left( {x - 5} \right)^4}\). Hỏi hàm số \(y = f\left( x \right)\) có mấy điểm cực trị?
\(5\).
\(2\).
\(4\).
\(3\).
