30 câu hỏi
Gọi \[A\], \[B\] là hai điểm cực trị của đồ thị hàm số \(y = - \frac{1}{3}{x^3} + x - \frac{2}{3}\). Tọa độ trung điểm của \(AB\) là
\(\left( {0;\frac{{ - 2}}{3}} \right)\).
\(\left( {1;0} \right)\).
\(\left( {0;1} \right)\).
\(\left( { - \frac{1}{3};\frac{2}{3}} \right)\).
Đồ thị hàm số \[y = - {x^3} - 3{x^2} + 1\] có điểm cực đại là
\(x = 0\).
\(\left( { - 2;\, - 19} \right)\).
\(\left( {0;\,1} \right)\).
\(x = - 2\).
Cho hàm số \[y = {x^3} - 3{x^2} + 5\]có đồ thị \[\left( C \right)\]. Điểm cực tiểu của đồ thị \[\left( C \right)\] là
\[M\left( {1;{\rm{ }}2} \right)\].
\[M\left( {5;{\rm{ }}0} \right)\].
\[M\left( {2;{\rm{ 1}}} \right)\].
\[M\left( {0;{\rm{ 5}}} \right)\].
Biết đồ thị \(\left( C \right)\) của hàm số \(y = \frac{{{x^2} - 4x + 5}}{{x - 1}}\) có hai điểm cực trị. Đường thẳng đi qua hai điểm cực trị của đồ thị \(\left( C \right)\) cắt trục hoành tại điểm \(M\) có hoành độ \({x_M}\) bằng
\({x_M} = 2\).
\({x_M} = 1 - \sqrt 2 \).
\({x_M} = 1\).
\({x_M} = 1 + \sqrt 2 \).
Tính số điểm cực trị của hàm số \(y = {x^4} - 2{x^3} + 2x\)
\(3\).
\[0\].
\[1\].
\(2\).
Cho hàm số \(f\left( x \right) = {\left( {{x^2} - 1} \right)^3}\). Số điểm cực trị của hàm số \(f\left( x \right)\) là
\(5\).
\(2\).
\[3\].
\(1\).
Giá trị cực tiểu \({y_{CT}}\) của hàm số \(y = x + \frac{4}{x} - 3\) là
\({y_{CT}} = - 3\).
\({y_{CT}} = 1\).
\({y_{CT}} = - 1\).
\({y_{CT}} = 3\).
Điểm cực tiểu của hàm số \[y = x\sqrt {4 - {x^2}} \] là
\( - 2\sqrt 3 \).
\(2\).
\( - \sqrt 2 \).
\(\sqrt 2 \).
Biết đồ thị hàm số \[y = {x^3} - 3x + 1\]có hai điểm cực trị là \[A\]và \[B\]. Phương trình đường thẳng \[AB\] là
\[y = - 2x + 1\].
\[y = 2x - 1\].
\[y = x - 2\].
\[y = - x + 2\].
Hàm số \(y = {\left( {{x^3} - 3x} \right)^e}\) có bao nhiêu điểm cực trị?
A. 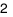 .
.
B. 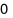 .
.
C. 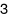 .
.
D. 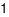 .
.
Cho hàm số \[y = a{x^3} + b{x^2} + cx + d\] có đồ thị như hình vẽ dưới
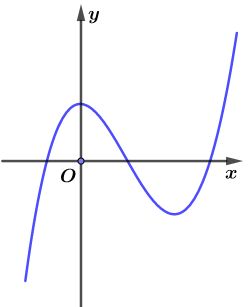
Hàm số đã cho có bao nhiêu điểm cực trị?
\(2\).
\(1\).
\(3\).
\(4\).
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình vẽ. Hàm số đạt cực tiểu tại các điểm

\(x = \pm \sqrt 2 \).
\(x = \pm 2\).
\(x = - 1\).
\(x = 3\).
Cho hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\)có đồ thị như hình vẽ bên dưới.
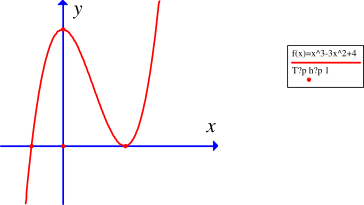
Mệnh đề nào sau đây sai?
Hàm số đạt cực tiểu tại \(x = 2\).
Hàm số đạt cực đại tại \(x = 4\).
Hàm số có hai điểm cực trị.
Hàm số đạt cực đại tại \(x = 0\).
Cho hàm số \(y = f\left( x \right)\)xác định, liên tục trên đoạn \(\left[ { - 2;2} \right]\)và có đồ thị là đường cong trong hình vẽ bên. Hàm số \(f\left( x \right)\)đạt cực tiểu tại điểm nào dưới đây?

\(x = - 1\).
\(x = 2\).
\(x = 1\).
\(x = - 2\).
Cho hàm số \(y = f(x)\) có đồ thị như hình bên. Hàm số có bao nhiêu điểm cực tiểu trên khoảng \(\left( {a;b} \right)\).
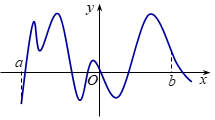
\(2\).
\(3\).
\(4\).
\(7\).
Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ { - \sqrt 3 ;\sqrt 3 } \right]\) và có đồ thị hàm số như hình vẽ sau
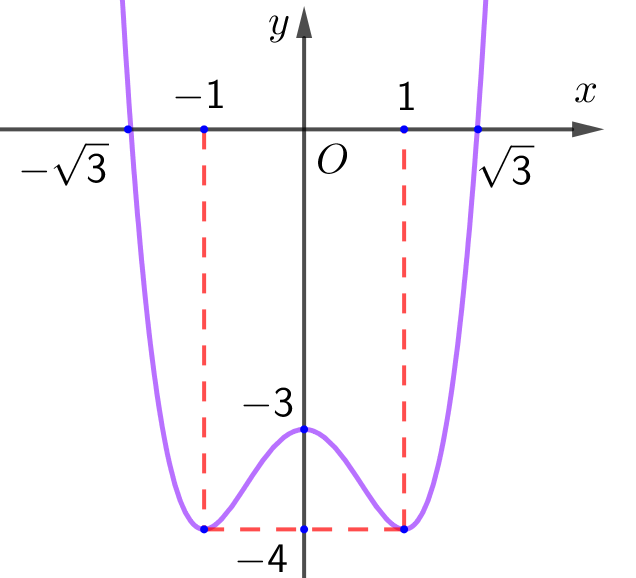
Điểm cực đại của đồ thị hàm số đã cho là
\(M\left( { - 1; - 4} \right)\).
\(N\left( {0; - 3} \right)\).
\(x = - 1\).
\(x = 0\).
Cho hàm số \(f\left( x \right)\) xác định, liên tục trên tập số thực \(\mathbb{R}\) và có đồ thị như hình bên. Hàm số \(y = f\left( x \right)\) đạt cực tiểu tại điểm nào dưới đây?
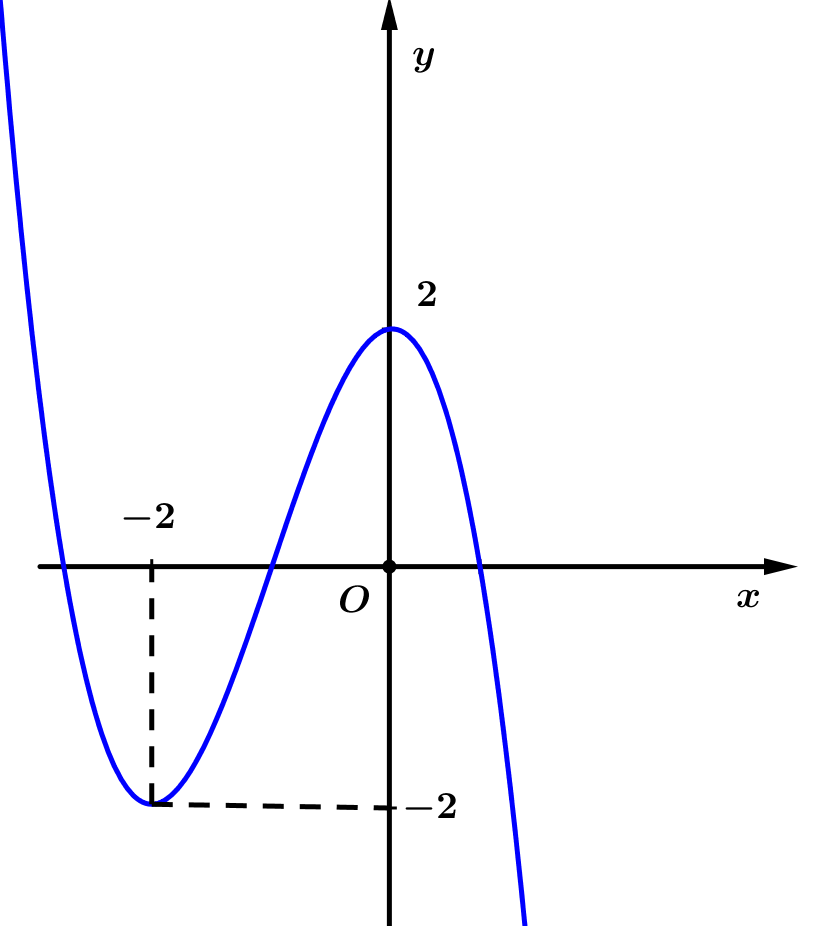
\(x = 1\).
\(x = 0\).
\(x = - 2\) và \(x = 0\).
\(x = - 2\).
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\;\)\(\left( {a,\;b,\;c,\;d \in \mathbb{R}} \right)\) có đồ thị như hình vẽ bên.
Số điểm cực trị của hàm số đã cho là
\(2\).
\(0\).
\(3\).
\(1\).
Cho hàm số \(f\left( x \right)\)liên tục trên đoạn \(\left[ { - 1;3} \right]\)và có đồ thị hàm số như hình vẽ bên:
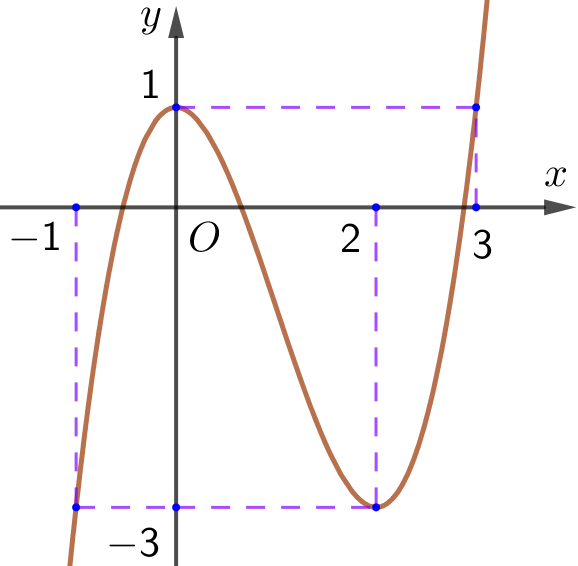
Hàm số đạt cực tiểu tại điểm
\(x = 2\).
\(x = 0\).
\(x = - 1\).
\(x = 3\).
Cho hàm số \(y = f(x)\) có đồ thị như hình vẽ. Hàm số \(f(x)\) có số điềm cực trị là
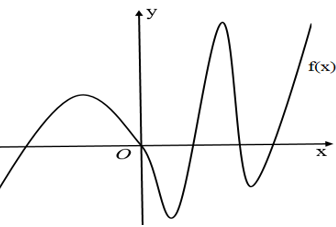
4.
3.
5.
6.
Cho hàm số \(y = f\left( x \right)\) có đạo hàm và liên tục trên \(\mathbb{R}\), có đồ thị như hình vẽ:
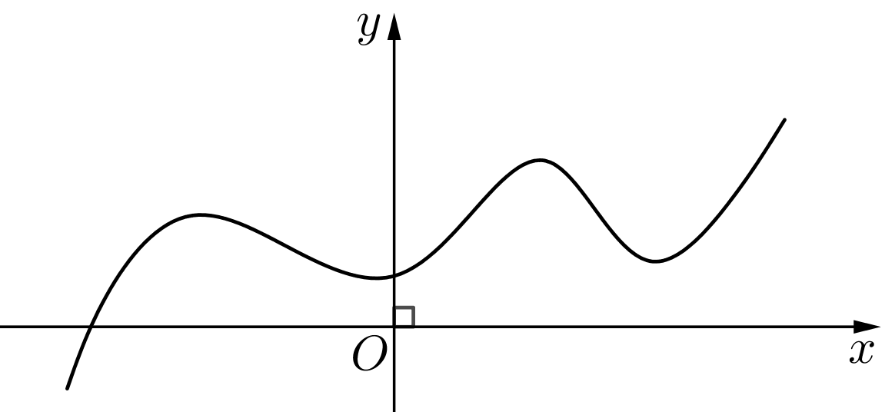
Số điểm cực trị của hàm số đã cho là
\(3\).
\(1\).
\(4\).
\(0\).
Cho hàm số \(f(x)\) xác định, liên tục trên \(\left[ { - 2;2} \right]\) và có đồ thị là đường cong trong hình vẽ bên. Hàm số \(f(x)\) đạt cực đại tại điểm nào dưới đây ?
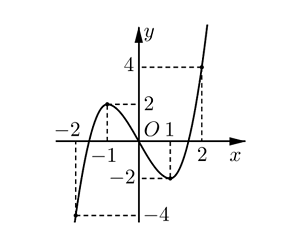
\(x = - 2\).
\(x = - 1\).
\(x = 1\).
\(x = 2\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Số điểm cực tiểu của hàm số là:

1.
\( - 2\).
\(4\).
0.
Cho hàm số \(y = f\left( x \right)\)có đồ thị như hình vẽ sau:
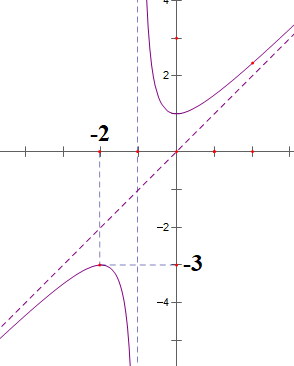
Giá trị cực tiểu của hàm số bằng
\(0\).
\( - 3\).
\( - 1\).
\(1\).
Cho hàm số \(y = f\left( x \right)\). Biết đồ thị của hàm số \( y = f'(x) \) như hình bên.
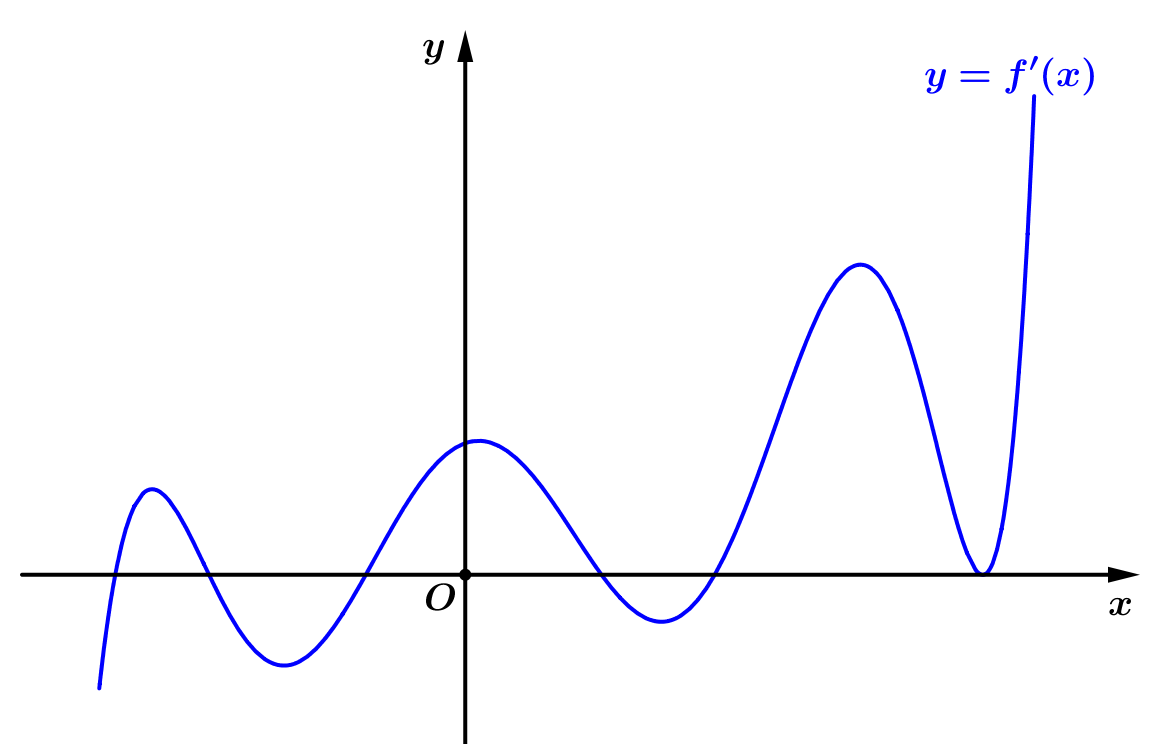
Tìm số cực tiểu của hàm số \(y = f\left( x \right)\)
\(5\).
\(4\).
\(3\).
\(2\).
Cho hàm số \[y = \,f\left( x \right)\] xác định trên đoạn \[\left[ {a\,;\,b\,} \right]\] có đồ thị hàm số \[y = \,f'\left( x \right)\] như hình vẽ
![Cho hàm số y = f(x) xác định trên đoạn [a;b] có đồ thị hàm số y = f'(x) như hình vẽSố điểm cực trị của hàm số y = f(x) (ảnh 1)](https://video.vietjack.com/upload2/images/1753358049/1753358115-image20.png)
Số điểm cực trị của hàm số \[y = \,f\left( x \right)\] trên đoạn \[\left[ {a\,;\,b\,} \right]\] là
4.
2.
3.
1.
Cho hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\) và có đồ thị của hàm số \(f'\left( x \right)\) như hình vẽ. Hàm số \(f\left( x \right)\) có mấy điểm cực trị?
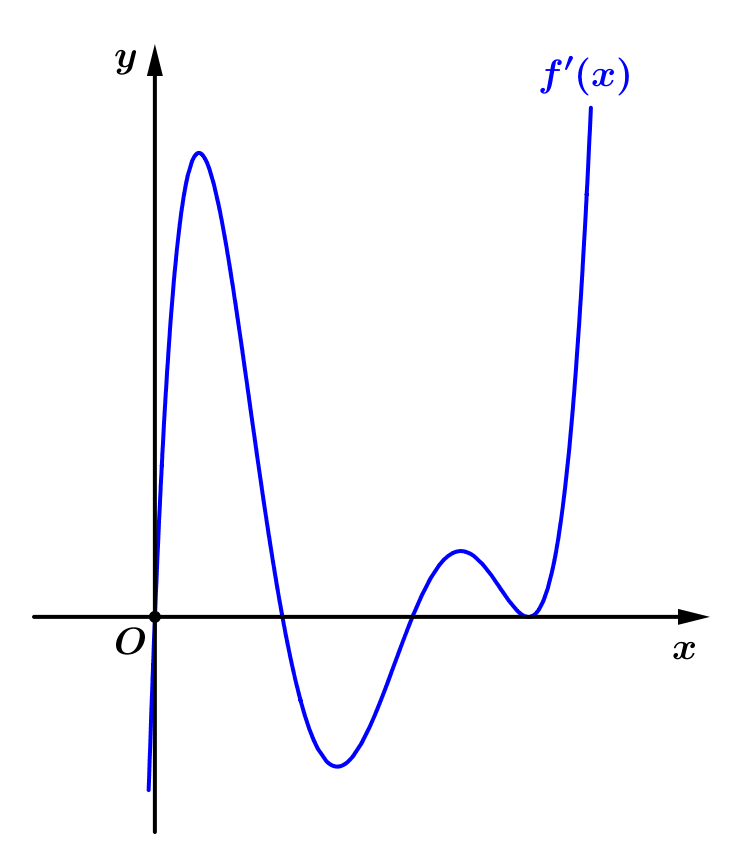
\(4\).
\(1\).
\(2\).
\(3\).
Cho hàm số \[y = f(x)\] có đạo hàm \[f'(x)\] trên \[\mathbb{R}\]. Đồ thị của hàm số \[y = f(x)\] như hình vẽ
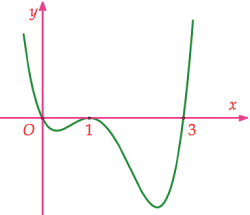
Đồ thị hàm số \[y = {\left( {f(x)} \right)^2}\] có bao nhiêu điểm cực đại, cực tiểu?
\(2\) điểm cực đại, \(3\) điểm cực tiểu.
\(2\) điểm cực tiểu, \(3\) điểm cực đại.
\(2\) điểm cực đại, \(2\) điểm cực tiểu.
\(1\) điểm cực đại, \(3\) điểm cực tiểu.
Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số \(y = f\left( x \right)\) là
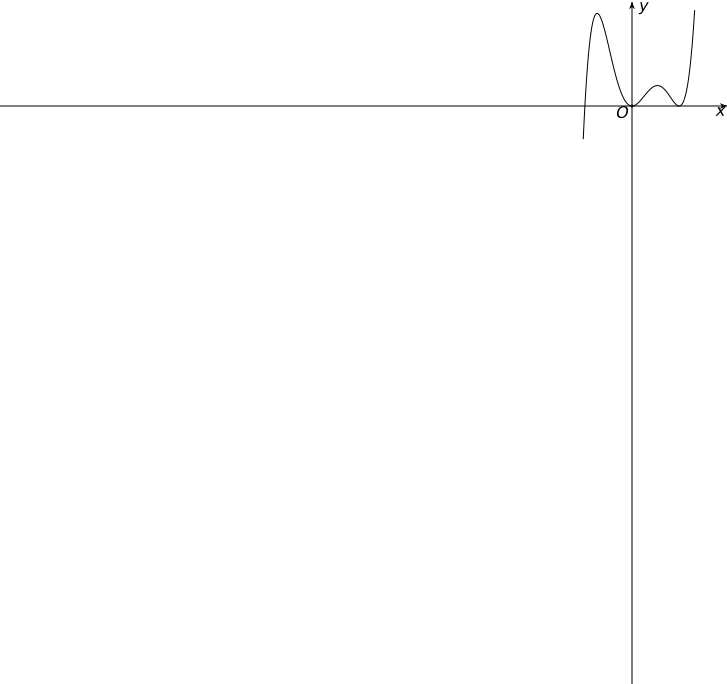
3.
4.
1.
2.
Cho hàm số \[y = f\left( x \right)\]xác định và liên tục trên \[\mathbb{R}\]và hàm số \[y = f'\left( x \right)\]có đồ thị như hình vẽ dưới đây
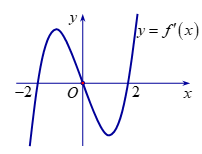
Khẳng định nào sau đây là đúng?
\(f\left( x \right)\)đạt cực đại tại \[x = 1\].
\(f\left( x \right)\)đạt cực đại tại \[x = 0\].
\(f\left( x \right)\)đạt cực đại tại \[x = - 1\].
\(f\left( x \right)\)đạt cực đại tại \[x = \pm 2\].
