30 câu hỏi
Tọa độ điểm cực đại của đồ thị hàm số \(y\, = \,{x^4}\, - \,2{x^2}\, + \,1\) là
\(\left( { - 1\,;\,0} \right)\).
\(\left( {1\,;\,0} \right)\).
\(\left( { - 1\,;\,0} \right)\) và \(\left( {1\,;\,0} \right)\).
\(\left( {0\,;\,1} \right)\).
Số điểm cực trị của đồ thị hàm số \(y = - {x^4} - 1\) là
\(2\).
\(0\).
\(1\).
\(3\).
Giá trị cực đại của hàm số \(y = {x^3} - 3x + 2\) bằng
\(0\).
\(1\).
\(4\).
\( - 1\).
Cho hàm số \(y = {x^3} - 3{x^2} + 1\). Độ dài đoạn thẳng nối hai điểm cực trị của đồ thị hàm số đã cho là
\(2\sqrt 5 \).
\(5\).
\(8\).
\(6\).
Tìm số điểm cực đại của đồ thị hàm số sau 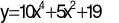
A. 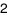 .
.
B. 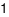 .
.
C. 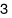 .
.
D. 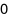 .
.
Hàm số \(y = {x^3} - 3{x^2} + 2x + 2019\)có bao nhiêu điểm cực trị
\(1\).
\(2\).
\(0\).
\(3\).
Giá trị cực tiểu của hàm số \(y = f\left( x \right) = - \frac{1}{3}{x^3} + x - 1\) là
\( - \frac{1}{3}\).
\( - 1\).
\( - \frac{5}{3}\).
\(1\).
Hàm số \(y = 2{x^3} - {x^2} + 5\) có điểm cực đại là
\(x = 5\).
\(x = 3\).
\(x = 0\).
\(x = \frac{1}{3}\).
Hàm số \(y = {x^3} - 3x + 2\) đạt cực đại tại điểm
\(x = 1\).
\(x = - 1\).
\(x = 0\).
\(x = 2\).
Hàm số \(y = \frac{{2x + 3}}{{x + 1}}\) có bao nhiêu điểm cực trị ?
\(3\).
\(0\).
\(1\).
\(2\).
Cho hàm số \(y = \frac{1}{3}{x^3} - {x^2} + \frac{1}{3}\). Giá trị cực tiểu của hàm số bằng
\( - 1\).
\(2\).
\(\frac{1}{3}\).
\(0\).
Số điểm cực trị của hàm số \(y = - \frac{4}{3}{x^3} - 2{x^2} - x - 3\) là
\(0\).
\(2\).
\(1\).
\(3\).
Gọi \({x_1}\)là điểm cực đại, \({x_2}\)là điểm cực tiểu của hàm số \(y = - {x^3} + 3x + 2\). Tính \({x_1} + 2{x_2}\).
\(2\).
\(1\).
\( - 1\).
\(0\).
Hàm số \[y = - {x^3} + 1\] có bao nhiêu điểm cực trị?
\(1\,.\)
\[0\,.\]
\[3\,.\].
\[2\,.\]
Hàm số \(y = {x^3} - 12x + 3\) đạt cực đại tại điểm
\(x = 19\).
\(x = - 2\).
\(x = 2\).
\(x = - 13\).
Hàm số \(y = {x^4} - 2{x^2} - 3\)có bao nhiêu điểm cực trị?
\(2\).
\(1\).
\(0\).
\(3\).
Hàm số \(y = {x^3} - 3{x^2} + 2\) đạt cực tiểu tại
\(x = - 2\).
\(x = 2\).
\(x = 0\).
\(x = 1\).
Cho hàm số \(f\left( x \right) = {x^4} - 8{x^3} + 1\). Chọn mệnh đề đúng.
Nhận điểm \(x = 6\)làm điểm cực đại.
Nhận điểm \(x = 6\)làm điểm cực tiểu.
Nhận điểm \(x = 0\)làm điểm cực đại.
Nhận điểm \(x = 0\)làm điểm cực tiểu.
Số điểm cực trị của hàm số \(y = \frac{{5x - 1}}{{x + 2}}\) là
1.
2.
0.
3.
Có bao nhiêu điểm cực trị của hàm số \(y = \frac{1}{x}\)?
\(3\).
\(2\).
\(0\).
\(1\).
Điểm cực đại của đồ thị hàm số \[y = - {x^3} + 6{x^2} - 9x + 4\] là:
\[\left( {1;0} \right)\].
\[\left( {3;4} \right)\].
\[\left( { - 1;0} \right)\].
\[\left( {2;2} \right)\].
Điểm cực đại của đồ thị hàm số \(y = {x^3} - 12x + 20\) là
\(\left( { - 2;0} \right)\).
\(\left( {2; - 4} \right)\).
\(\left( {2;36} \right)\).
\(\left( { - 2;36} \right)\).
Hàm số nào sau đây không có cực trị:
\(y = {x^2} - 3x\).
\(y = \frac{{3x + 1}}{{2x - 1}}\).
\(y = {x^3} - 3x + 1\).
\(y = {x^4} + 2x\).
Hàm số \(y = {x^3} - 3{x^2} + 2\)đạt cực tiểu tại:
\(x = - 2\).
\(x = 2\).
\(x = 0\).
\(x = 1\).
Hàm số nào trong 4 hàm số được liệt kê dưới đây không có cực trị?
\(y = {x^4} + 2{x^2} - 1\).
\(y = {x^2} - 1\).
\(y = {x^3} + 3{x^2} - 21\).
\(y = {x^3} + x + 1\).
Hàm số nào sau đây có cực trị?
\(y = \sqrt {x - 1} \) .
\(y = {x^2} - 2x + 3\).
\(y = {x^3} + 8x + 9\) .
\(y = \frac{{2x - 1}}{{3x + 1}}\) .
Hàm số \(y = {x^3} - 3x + 2\) đạt cực đại đại tại điểm.
\(x = - 1\).
\(x = 0\).
\(x = 1\).
\(x = - 2\).
Cho hàm số \[y = {x^3} - 3{x^2} - 9x + 1\]có đồ thị \(\left( C \right)\). Gọi \(A\left( {{x_1};{y_1}} \right)\) và \(B\left( {{x_2};{y_2}} \right)\)lần lượt là điểm cực đại và cực tiểu của đồ thị hàm số \(\left( C \right)\). Tính tổng \(S = {x_1} + {x_2}\)
\(S = - 3\).
\(S = - 2\).
\(S = 2\).
\(S = 3\).
Biết đồ thị \(\left( C \right)\) của hàm số \(y = \frac{{{x^2} - 2x + 3}}{{x - 1}}\) có hai điểm cực trị. Đường thẳng đi qua hai điểm cực trị của đồ thị \(\left( C \right)\) cắt trục hoành tại điểm \(M\) có hoành độ \({x_M}\) bằng:
\({x_M} = 1 - \sqrt 2 \).
\({x_M} = - 2\).
\({x_M} = 1\).
\({x_M} = 1 + \sqrt 2 \).
Giá trị cực đại của hàm số \(y = \frac{{{x^2} + x + 1}}{{x + 1}}\)là
\( - 2\).
\( - 3\).
\(1\).
\(0\).
