29 câu hỏi
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = x{\left( {x - 2} \right)^3}{\left( {x - 3} \right)^{2020}}\). Số điểm cực trị của hàm số \(y = f\left( x \right)\) là
\(3\).
\(1\).
\(4\).
\(2\).
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {x^{2021}}{\left( {x - 1} \right)^2}{\left( {x + 2} \right)^3},\forall x \in \mathbb{R}\). Số điểm cực trị của hàm số đã cho là
\(3\).
\(2\).
\(6\).
\(1\).
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = x\left( {x - 1} \right){\left( {x + 2} \right)^3}\), \(\forall x \in \mathbb{R}\). Số điểm cực trị của hàm số đã cho là
\(3\).
\(2\).
\(5\).
\(1\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\), có đạo hàm \(f'\left( x \right) = x{\left( {x - 1} \right)^2}{\left( {x + 1} \right)^2}\). Hàm số đã cho có bao nhiêu điểm cực trị?
Có đúng \(3\) điểm cực trị.
Không có điểm cực trị.
Có đúng \(1\) điểm cực trị.
Có đúng \(2\) điểm cực trị.
Cho hàm số \(y = f\left( x \right)\) liên tục và có đạo hàm \(f'\left( x \right) = {\left( {2x - 1} \right)^4}\left( {x + 2} \right)\left( {3 - 3x} \right)\), số điểm cực trị của hàm số là
\(1\).
\(2\).
\(3\).
\(0\).
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {x - 1} \right)\left( {{x^2} - 3x + 2} \right),{\rm{ }}\forall x \in \mathbb{R}\). Số điểm cực trị của hàm số \(f\left( x \right)\) là
\(1\).
\(2\).
\(0\).
\(3\).
Cho hàm số \(f\left( x \right)\) có \(f'\left( x \right) = {x^{2017}}{\left( {x - 1} \right)^{2018}}{\left( {x + 1} \right)^{2019}}\), hỏi hàm số đã cho có bao nhiêu cực trị?
\(0\).
\(1\).
\(2\).
\(3\).
Cho hàm số \(y = f\left( x \right)\)có đạo hàm \(f'\left( x \right) = x\left( {x - 1} \right){\left( {{x^2} + x - 2} \right)^3},\,\,\forall x \in \mathbb{R}\). Số điểm cực trị của hàm số đã cho là:
\(3\).
\(2\).
\(5\).
\(1\).
Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\) và có đạo hàm là \(f'(x) = {x^2}({x^2} - 4)({x^2} - 3x + 2)(x - 3)\). Hàm số có bao nhiêu điểm cực đại ?
3.
0.
2.
1.
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = x{\left( {x + 2} \right)^2}\left( {{2^x} - 4} \right),\forall x \in \mathbb{R}\). Số điểm cực trị của hàm số đã cho là
\(3\).
\(1\).
\(2\).
\(0\).
Tọa độ điểm cực đại của đồ thị hàm số \[y = {2^{\frac{x}{{4{x^2} + 1}}}}\] là
\[\left( { - \frac{1}{2}\,;\,\sqrt[4]{2}} \right)\].
\[\left( { - \frac{1}{2}\,;\, - \sqrt[4]{2}} \right)\].
\[\left( {\frac{1}{2}\,;\,\sqrt[4]{2}} \right)\].
\[\left( { - \frac{1}{2}\,;\,\frac{1}{{\sqrt[4]{2}}}} \right)\].
Nếu hàm số \(y = f\left( x \right)\)thỏa mãn \(f'\left( x \right) = {\left( {x - 1} \right)^3}\left( {{2^x} - 2} \right){\log _2}x\), \(\forall x > 0\)thì
Trên khoảng \(\left( {0; + \infty } \right)\)hàm số \(y = f\left( x \right)\)không có điểm cực trị nào.
Trên khoảng \(\left( {0; + \infty } \right)\)hàm số \(y = f\left( x \right)\)có điểm cực tiểu là \(x = 1\).
Trên khoảng \(\left( {0; + \infty } \right)\)hàm số \(y = f\left( x \right)\)có điểm cực đại là \(x = 1\).
Trên khoảng \(\left( {0; + \infty } \right)\)hàm số \(y = f\left( x \right)\)có nhiều hơn một điểm cực trị.
Cho hàm số \(y = \ln \left( {2{x^2} - {x^4}} \right)\). Mệnh đề nào sau đây đúng?
Hàm số đạt cực tiểu tại \(x = 1\).
Hàm số đạt cực tiểu tại \(x = - 1\).
Hàm số có hai cực trị.
Hàm số có ba cực trị.
Cho hàm số \(y = {x^2}.{{\rm{e}}^{ - x}}\). Khẳng định nào sau đây là đúng?
Hàm số không có điểm cực trị.
Hàm số chỉ có điểm cực tiểu, không có điểm cực đại.
Hàm số đạt cực đại tại \(x = 0\)và đạt cực tiểu tại \(x = 2\).
Hàm số đạt cực tiểu tại \(x = 0\)và đạt cực đại tại \(x = 2\).
Điểm cực đại của hàm số \(y = \left( {2x + 1} \right){{\mathop{\rm e}\nolimits} ^{1 - x}}\) là
\(x = - 1\).
\(x = \frac{1}{2}\).
\(x = 1\).
\(x = \frac{3}{2}\).
Cho hàm số \(y = x - \ln \left( {1 + x} \right)\). Mệnh đề nào sau đây đúng?
Hàm số đồng biến trên khoảng \(\left( { - 1;\,0} \right)\).
Hàm số đạt cực đại tại \(x = 0\).
Hàm số đồng biến trên khoảng \(\left( { - 1;\, + \infty } \right)\).
Hàm số đạt cực tiểu tại \(x = 0\).
Cho hàm số \(y = \ln \left( {2x - {x^2}} \right)\). Mệnh đề nào sau đây đúng?
Hàm số đạt cực tiểu tại \(x = 1\).
Hàm số đạt cực đại tại \(x = 1\).
Hàm số có hai cực trị.
Hàm số không có cực trị.
Hàm số \(f\left( x \right) = x{{\rm{e}}^{ - x}}\) đạt cực trị tại điểm
\(x = e\).
\(x = {e^2}\).
\(x = 1\).
\(x = 2\).
Hàm số \(y = {x^2}\ln x\) đạt cực trị tại điểm
\(x = \sqrt {\rm{e}} \).
\(x = 0\); \(x = \frac{1}{{\sqrt {\rm{e}} }}\).
\(x = 0\).
\(x = \frac{1}{{\sqrt {\rm{e}} }}\).
Giá trị cực tiểu của hàm số \(y = {e^x}\left( {{x^2} - 3} \right)\) là:
\(\frac{6}{e}\).
\(\frac{6}{{{e^3}}}\).
\( - 3e\).
\( - 2e\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \) \[\left( {\ln x + 1} \right)\left( {{e^x} - 2019} \right)\left( {x + 1} \right)\] trên khoảng \(\left( {0; + \infty } \right)\). Hỏi hàm số \(y = f\left( x \right)\) có bao nhiêu điểm cực trị?
\(2\).
\(3\).
\(0\).
\(1\).
Hàm số \(y = \ln \left( {{x^3} - 3{x^2} + 1} \right)\)có bao nhiêu điểm cực trị?
\(2\).
\(3\).
\(0\).
\(1\).
Số điểm cực trị của hàm \(y = x{e^x} - {e^x} - \frac{{{x^2}}}{2} + 2\) là
\(1\).
\(3\).
\(0\).
\(2\).
Cho hàm số \(y = {x^2}\ln x\). Mệnh đề nào sau đây là đúng?
Hàm số đạt cực tiểu tại \(x = \sqrt e \).
Hàm số đạt cực tiểu tại \(x = \frac{1}{{\sqrt e }}\).
Hàm số đạt cực đại tại \(x = \sqrt e \).
Hàm số đạt cực đại tại \(x = \frac{1}{{\sqrt e }}\).
Cho hàm số \(y = f\left( x \right)\). Đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ dưới đây
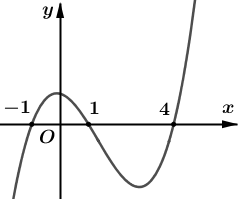
Số điểm cực trị của hàm số \(g\left( x \right) = {e^{2f\left( x \right) + 1}} + {5^{f\left( x \right)}}\) là
\(1\).
\(2\).
\(3\).
\(4\).
Cho hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ bên:
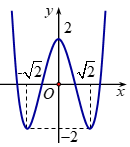
Tìm số điểm cực trị của hàm số \(y = {3^{f\left( x \right)}} + {2^{f\left( x \right)}}\).
\(2\).
\(3\).
\(5\).
\(4\).
Cho hàm số bậc năm \(y = f(x)\) liên tục trên \(\mathbb{R}\) và có đồ thị hàm số \(y = f'(x)\) như trong hình vẽ bên.
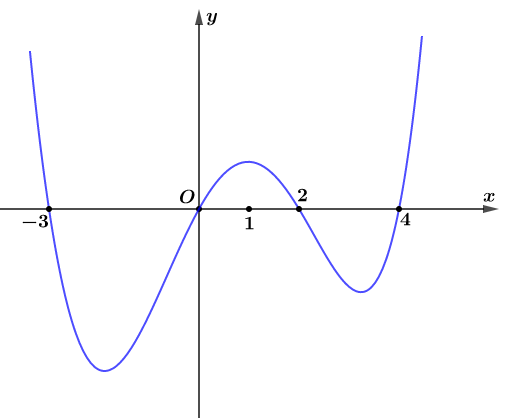
Tìm số điểm cực đại của hàm số \(y = {e^{f(x)}}.{\pi ^{{f^3}(x)}}\).
\(1\).
\(0\).
\(2\).
\(3\).
Cho hàm số \[f\left( x \right)\] có đồ thị như hình dưới đây
Hàm số \[g\left( x \right) = \ln \left( {f\left( x \right)} \right)\] có bao nhiêu điểm cực trị ?
\[0\].
\[1\].
\[2\].
\[3\].
Cho hàm số \[y = f\left( x \right)\]. Biết hàm số \[y = f'\left( x \right)\] có đồ thị như hình vẽ bên dưới. Số điểm cực trị của hàm số \[y = {2021^{f\left( x \right)}} + {2020^{f\left( x \right)}}\] là
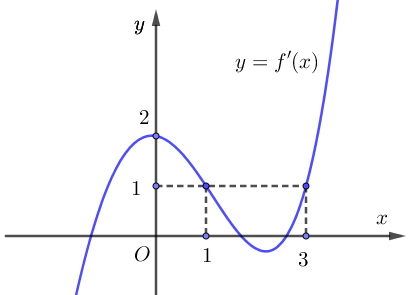
\[2.\]
\[5\].
\[3\].
\[4\].
