186 câu hỏi
Cho hàm số 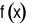 đồng biến trên tập số thực
đồng biến trên tập số thực  , mệnh đề nào sau đây là đúng?
, mệnh đề nào sau đây là đúng?
C. Với mọi 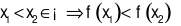 .
.
Với mọi 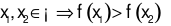 .
.
B.
Với mọi 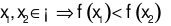 .
.
Với mọi 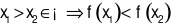 .
.
Cho hàm số \(f\left( x \right)\)đồng biến trên tập số thực \(\mathbb{R}\), mệnh đề nào sau đây là đúng?
Với mọi \({x_1},{x_2} \in \mathbb{R} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\).
Với mọi \({x_1},{x_2} \in \mathbb{R} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
>
Với mọi \({x_1} < {x_2} \in \mathbb{R} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
>
Với mọi \({x_1} > {x_2} \in \mathbb{R} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
>
Cho hàm số \(f\left( x \right)\)đồng biến trên tập số thực \(\mathbb{R}\), mệnh đề nào sau đây là đúng?
Với mọi \({x_1},{x_2} \in \mathbb{R} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\).
Với mọi \({x_1},{x_2} \in \mathbb{R} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
Với mọi \({x_1} < {x_2} \in \mathbb{R} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
Với mọi \({x_1} > {x_2} \in \mathbb{R} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
Cho hàm số 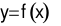 có đạo hàm trên
có đạo hàm trên  thỏa mãn
thỏa mãn 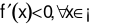 . Khẳng định nào sau đây là đúng?
. Khẳng định nào sau đây là đúng?
C.  .
.
B.
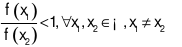 .
.
D.
 .
.
Cho hàm số \(y = f\left( x \right)\)có đạo hàm trên \(\mathbb{R}\)thỏa mãn \(f'\left( x \right) < 0,\;\forall x \in \mathbb{R}\). Khẳng định nào sau đây là đúng?
>
\(\frac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} > 0,\;\forall {x_1},{x_2} \in \mathbb{R},{x_1} \ne {x_2}\).
\(\frac{{f\left( {{x_1}} \right)}}{{f\left( {{x_2}} \right)}} < 1,\;\forall {x_1},{x_2} \in \mathbb{R},{x_1} \ne {x_2}\).
>
\(\frac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} < 0,\;\forall {x_1},{x_2} \in \mathbb{R},{x_1} \ne {x_2}\).
>
\(f\left( {{x_1}} \right) < f\left( {{x_2}} \right),\;\forall {x_1},{x_2} \in \mathbb{R},{x_1} \ne {x_2}\).
>
Cho hàm số \(y = f\left( x \right)\)có đạo hàm trên \(\mathbb{R}\) thỏa mãn \(f'\left( x \right) < 0,\;\forall x \in \mathbb{R}\). Khẳng định nào sau đây là đúng?
\(\frac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} > 0,\;\forall {x_1},{x_2} \in \mathbb{R},{x_1} \ne {x_2}\).
\(\frac{{f\left( {{x_1}} \right)}}{{f\left( {{x_2}} \right)}} < 1,\;\forall {x_1},{x_2} \in \mathbb{R},{x_1} \ne {x_2}\).
\(\frac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} < 0,\;\forall {x_1},{x_2} \in \mathbb{R},{x_1} \ne {x_2}\).
\(f\left( {{x_1}} \right) < f\left( {{x_2}} \right),\;\forall {x_1},{x_2} \in \mathbb{R},{x_1} \ne {x_2}\).
Cho 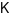 là một khoảng, nửa khoảng hoặc một đoạn. Hàm số
là một khoảng, nửa khoảng hoặc một đoạn. Hàm số 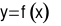 liên tục và xác định trên
liên tục và xác định trên 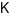 . Mệnh đề nào không đúng?
. Mệnh đề nào không đúng?
B. Nếu 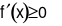 ,
, 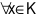 thì hàm số
thì hàm số 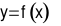 đồng biến trên
đồng biến trên 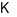 .
.
Nếu hàm số 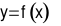 đồng biến trên
đồng biến trên 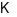 thì
thì 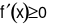 ,
, 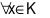 .
.
Nếu hàm số 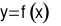 là hàm số hằng trên
là hàm số hằng trên 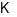 thì
thì 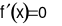 ,
, 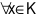 .
.
Nếu 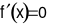 ,
, 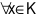 thì hàm số
thì hàm số 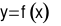 không đổi trên
không đổi trên 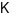 .
.
Cho \(K\) là một khoảng, nửa khoảng hoặc một đoạn. Hàm số \(y = f\left( x \right)\) liên tục và xác định trên \(K\). Mệnh đề nào không đúng?
Nếu hàm số \(y = f\left( x \right)\) đồng biến trên \(K\) thì \(f'\left( x \right) \ge 0\), \(\forall x \in K\).
Nếu \(f'\left( x \right) \ge 0\), \(\forall x \in K\) thì hàm số \(y = f\left( x \right)\) đồng biến trên \(K\).
Nếu hàm số \(y = f\left( x \right)\) là hàm số hằng trên \(K\) thì \(f'\left( x \right) = 0\), \(\forall x \in K\).
Nếu \(f'\left( x \right) = 0\), \(\forall x \in K\) thì hàm số \(y = f\left( x \right)\) không đổi trên \(K\).
Cho \(K\) là một khoảng, nửa khoảng hoặc một đoạn. Hàm số \(y = f\left( x \right)\) liên tục và xác định trên \(K\). Mệnh đề nào không đúng?
Nếu hàm số \(y = f\left( x \right)\) đồng biến trên \(K\) thì \(f'\left( x \right) \ge 0\), \(\forall x \in K\).
Nếu \(f'\left( x \right) \ge 0\), \(\forall x \in K\) thì hàm số \(y = f\left( x \right)\) đồng biến trên \(K\).
Nếu hàm số \(y = f\left( x \right)\) là hàm số hằng trên \(K\) thì \(f'\left( x \right) = 0\), \(\forall x \in K\).
Nếu \(f'\left( x \right) = 0\), \(\forall x \in K\) thì hàm số \(y = f\left( x \right)\) không đổi trên \(K\).
Cho hàm số 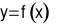 liên tục trên
liên tục trên  và có đồ thị như hình vẽ bên dưới. Hàm số nghịch biến trên khoảng nào dưới đây?
và có đồ thị như hình vẽ bên dưới. Hàm số nghịch biến trên khoảng nào dưới đây?
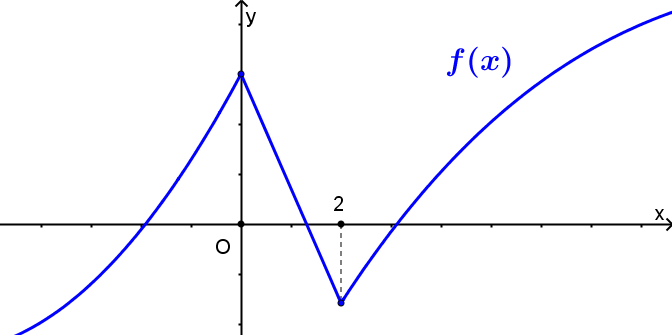
B.
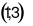 .
.
C. 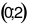 .
.
D.
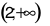 .
.
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên dưới. Hàm số nghịch biến trên khoảng nào dưới đây?
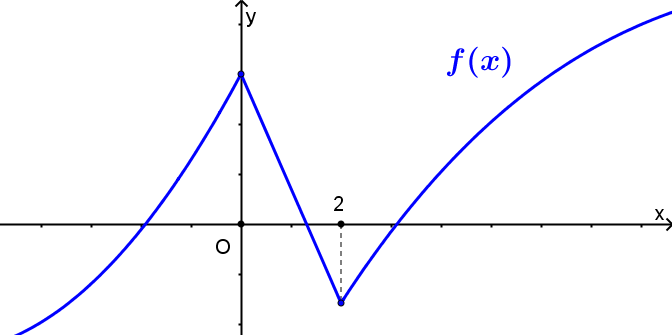
\(\left( { - \infty ;0} \right)\).
\(\left( {1;3} \right)\).
\(\left( {0;2} \right)\).
\(\left( {2; + \infty } \right)\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên dưới. Hàm số nghịch biến trên khoảng nào dưới đây?
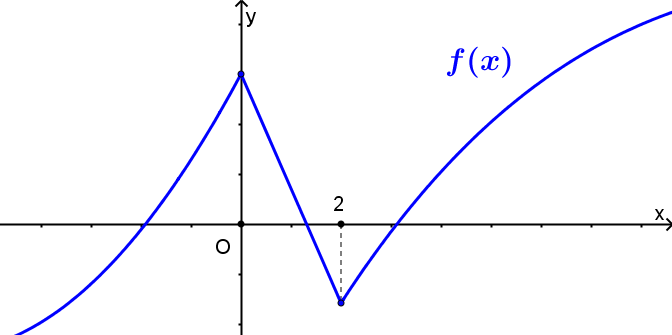
\(\left( { - \infty ;0} \right)\).
\(\left( {1;3} \right)\).
\(\left( {0;2} \right)\).
\(\left( {2; + \infty } \right)\).
Hàm số 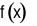 đồng biến trên khoảng
đồng biến trên khoảng 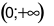 , khẳng định nào sau đây đúng?
, khẳng định nào sau đây đúng?
B.
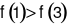 .
.
C.
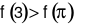 .
.
D. 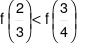 .
.
Hàm số \(f\left( x \right)\) đồng biến trên khoảng \(\left( {0\,;\, + \infty } \right)\), khẳng định nào sau đây đúng?
\(f\left( 2 \right) > f\left( { - 1} \right)\).
\(f\left( 1 \right) > f\left( 3 \right)\).
\(f\left( 3 \right) > f\left( \pi \right)\).
\(f\left( {\frac{2}{3}} \right) < f\left( {\frac{3}{4}} \right)\).
>
Hàm số \(f\left( x \right)\) đồng biến trên khoảng \(\left( {0\,;\, + \infty } \right)\), khẳng định nào sau đây đúng?
\(f\left( 2 \right) > f\left( { - 1} \right)\).
\(f\left( 1 \right) > f\left( 3 \right)\).
\(f\left( 3 \right) > f\left( \pi \right)\).
\(f\left( {\frac{2}{3}} \right) < f\left( {\frac{3}{4}} \right)\).
Cho hàm số 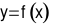 có đạo hàm trên khoảng
có đạo hàm trên khoảng 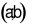 . Mệnh đề nào sau đây đúng.
. Mệnh đề nào sau đây đúng.
A. Nếu  thì hàm số đồng biến trên khoảng
thì hàm số đồng biến trên khoảng 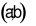 .
.
Nếu  thì hàm số đồng biến trên khoảng
thì hàm số đồng biến trên khoảng 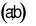 .
.
Nếu  thì hàm số đồng biến trên khoảng
thì hàm số đồng biến trên khoảng 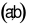 .
.
Nếu  thì hàm số đồng biến trên khoảng
thì hàm số đồng biến trên khoảng 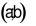 .
.
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên khoảng \(\left( {a{\kern 1pt} ;{\kern 1pt} b} \right)\). Mệnh đề nào sau đây đúng.
Nếu \(f'\left( x \right) > 0,\forall x \in \left( {a;b} \right)\) thì hàm số đồng biến trên khoảng \(\left( {a{\kern 1pt} ;{\kern 1pt} b} \right)\).
Nếu \(f'\left( x \right) < 0,\forall x \in \left( {a;b} \right)\) thì hàm số đồng biến trên khoảng \(\left( {a{\kern 1pt} ;{\kern 1pt} b} \right)\).
>
Nếu \(f\left( x \right) < 0,\forall x \in \left( {a;b} \right)\) thì hàm số đồng biến trên khoảng \(\left( {a{\kern 1pt} ;{\kern 1pt} b} \right)\).
>
Nếu \(f\left( x \right) > 0,\forall x \in \left( {a;b} \right)\) thì hàm số đồng biến trên khoảng \(\left( {a{\kern 1pt} ;{\kern 1pt} b} \right)\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên khoảng \(\left( {a{\kern 1pt} ;{\kern 1pt} b} \right)\). Mệnh đề nào sau đây đúng.
Nếu \(f'\left( x \right) > 0,\forall x \in \left( {a;b} \right)\) thì hàm số đồng biến trên khoảng \(\left( {a{\kern 1pt} ;{\kern 1pt} b} \right)\).
Nếu \(f'\left( x \right) < 0,\forall x \in \left( {a;b} \right)\) thì hàm số đồng biến trên khoảng \(\left( {a{\kern 1pt} ;{\kern 1pt} b} \right)\).
Nếu \(f\left( x \right) < 0,\forall x \in \left( {a;b} \right)\) thì hàm số đồng biến trên khoảng \(\left( {a{\kern 1pt} ;{\kern 1pt} b} \right)\).
Nếu \(f\left( x \right) > 0,\forall x \in \left( {a;b} \right)\) thì hàm số đồng biến trên khoảng \(\left( {a{\kern 1pt} ;{\kern 1pt} b} \right)\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và \(y = f'\left( x \right) < 0,\forall x \in \left( { - 3;5} \right)\). Khẳng định nào sau đây đúng?
\(f\left( { - 2} \right) = f\left( 2 \right)\).
\(f\left( { - 3} \right) > f\left( 5 \right)\).
\(f\left( { - 3} \right) < f\left( 5 \right)\).
\(f\left( 0 \right) < f\left( 5 \right)\).
Cho hàm số \[f(x)\]nghịch biến trên \[R\]. Hàm số nào sau đây có thể không nghịch biến trên R?
\(f(x) + 2020\).
\(f(x) - 2019\).
\(f(x) - {x^2}\).
\(f(x) - x\).
Đường cong ở hình bên là đồ thị của hàm số \(y = \frac{{ax + b}}{{cx + d}}\) với \[a\], \[b\], \[c\], \[d\] là các số thực
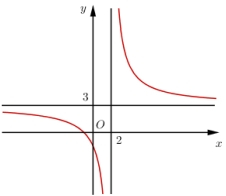
Mệnh đề nào dưới đây đúng?
\(y' > 0\), \(\forall x \ne 2\).
\(y' > 0\), \(\forall x \ne 3\).
\(y' < 0\), \(\forall x \ne 2\).
\(y' < 0\), \(\forall x \ne 3\).
Cho hàm số \(f\left( x \right) = \frac{{x - 1}}{{x - 3}}.\) Khẳng định nào sau đây là đúng?
Hàm số nghịch biến trên từng khoảng xác định.
Hàm số nghịch biến trên \(\mathbb{R}.\)
Hàm số đồng biến trên từng khoảng xác định.
Hàm số đồng biến trên \(\mathbb{R}.\)
Cho hàm số \(y = - \frac{1}{3}{x^3} + \frac{1}{2}{x^2} + 6x - 1\). Mệnh đề nào dưới đây đúng?
Hàm số đồng biến trên khoảng \(\left( { - 2;\,3} \right)\).
Hàm số đồng biến trên khoảng \(\left( {3;\, + \infty } \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - 2;\,3} \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - \infty ;\,0} \right)\).
Khoảng đồng biến của hàm số \(y = {x^4} + 4x - 6\) là
\(\left( { - 1;\; + \infty } \right)\).
\(\left( { - \infty ;\; - 9} \right)\).
\(\left( { - 9;\; + \infty } \right)\).
\(\left( { - \infty ;\; - 1} \right)\).
Hàm số nào dưới đây đồng biến trên khoảng \(\left( { - \infty ; + \infty } \right)\)?
\(y = \frac{{x + 1}}{{x + 3}}\).
\(y = {x^3} + x\).
\(y = \frac{{x - 1}}{{x - 2}}\).
\(y = - {x^3} - 3x\).
Trong các hàm số sau hàm nào đồng biến trên \(\mathbb{R}\)?
\(y = {x^4} + {x^2} - 1\).
\(y = \frac{{x + 1}}{{x + 3}}\).
\(y = {x^2} + 1\).
\(y = {x^3} + x\).
Cho hàm số \(y = \frac{{x + 1}}{{x - 1}}.\) Khẳng định nào sau đây là đúng?
Hàm số đã cho nghịch biến trên khoảng \(\left( { - \infty ;1} \right)\).
Hàm số đã cho đồng biến trên khoảng \(\left( { - \infty ;1} \right)\) và khoảng \(\left( {1; + \infty } \right)\).
Hàm số đã cho đồng biến trên khoảng \(\left( {0; + \infty } \right)\).
Hàm số đã cho nghịch biến trên tập \(\mathbb{R}\backslash \left\{ 1 \right\}\).
Cho hàm số \(y = {x^4} - 8{x^2} + 2019\). Mệnh đề nào sau đây sai:
Hàm số nghịch biến trên khoảng \(\left( { - \infty \,;\,2} \right)\).
Hàm số nghịch biến trên khoảng \(\left( {0\,;\,2} \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - \infty \,;\, - 2} \right)\).
Hàm số đồng biến trên khoảng \(\left( {2\,;\, + \infty } \right)\).
Các khoảng đồng biến của hàm số \(y = {x^4} + 2{x^2} - 3\) là
\(\left( { - 1;0} \right)\) và \(\left( {1; + \infty } \right)\).
\(\left( { - \infty ; - 1} \right)\) và \(\left( {0;1} \right)\).
\(\left( {0; + \infty } \right)\).
\(\left( { - \infty ;0} \right)\).
Trong các hàm số sau, hàm số nào đồng biến trên \[\mathbb{R}\]?
\(y = {x^3} - x\).
\(y = {x^2} + 1\).
\(y = {x^4} + 2{x^2}\).
\(y = {x^3} + x\).
Hàm số \(y = - {x^4} + 2{x^2} + 1\) đồng biến trên khoảng nào dưới đây?
\(\left( { - \infty \,;\,0} \right)\).
\(\left( {0\,;\, + \infty } \right)\).
\(\left( {1\,;\, + \infty } \right)\).
\(\left( { - \infty \,;\, - 1} \right)\).
Kết luận nào sau đây về tính đơn điệu của hàm số \(y = \frac{{2x + 1}}{{x - 1}}\) là đúng?
Hàm số nghịch biến trên \(\mathbb{R}\backslash \left\{ 1 \right\}\).
Hàm số đồng biến trên \(\mathbb{R}\backslash \left\{ 1 \right\}\).
Hàm số nghịch biến trên \(\left( { - \infty ;\,1} \right)\) và \(\left( {1;\, + \infty } \right)\).
Hàm số đồng biến trên \(\left( { - \infty ;\,1} \right)\) và \(\left( {1;\, + \infty } \right)\).
Tìm khoảng đồng biến của hàm số \(y = - {x^3} + 6{x^2} - 9x + 4\).
\((2; + \infty )\).
\((1;3)\).
\((0;3)\).
\(( - \infty ;0)\).
Cho hàm số \(f\left( x \right) = \frac{{3x + 1}}{{ - x + 1}}\). Trong các mệnh đề sau mệnh đề nào đúng ?
\(f\left( x \right)\) nghịch biến trên \(\mathbb{R}\).
\(f\left( x \right)\) đồng biến trên \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\).
\(f\left( x \right)\) nghịch biến trên \(\left( { - \infty ; - 1} \right) \cup \left( {1; + \infty } \right)\).
\(f\left( x \right)\) đồng biến trên \(\mathbb{R}\).
Hàm số \(y = {x^3} - 3{x^2} - 9x + 7\) đồng biến trên khoảng nào sau đây?
\(\left( {1\,; + \infty } \right).\)
\(\left( { - 5\,; - 2} \right).\)
\(\left( { - \infty \,;1} \right).\)
\(\left( { - 1\,;3} \right).\)
Khoảng nghịch biến của hàm số \[y = {x^3} + 3{x^2} + 4\] là
\[\left( { - \infty ; - 2} \right)\] và \[\left( {0; + \infty } \right)\].
\[\left( { - \infty ;0} \right)\].
\[\left( {2; + \infty } \right)\].
\[\left( { - 2;0} \right)\].
Cho hàm số \(y = \frac{{x + 3}}{{x + 2}}\). Khẳng định nào sau đây là đúng.
Hàm số đồng biến trên \(\mathbb{R}\).
Hàm số đồng biến trên\(\left( { - \infty ; - 2} \right)\) và \(\left( { - 2; + \infty } \right)\).
Hàm số nghịch biến trên \(\mathbb{R}{\rm{\backslash }}\left\{ { - 2} \right\}\).
Hàm số nghịch biến trên \(\left( { - \infty ; - 2} \right)\)và \(\left( { - 2; + \infty } \right)\).
Cho hàm số \[y = - {x^3} + 3{x^2} + 9x - 1\]. Mệnh đề nào sau đây đúng?
Hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ;\, - 1} \right)\), \(\left( {3;\, + \infty } \right)\); nghịch biến trên \(\left( { - 1;\,3} \right)\).
Hàm số đồng biến trên \(\left( { - 1;\,3} \right)\), nghịch biến trên \(\left( { - \infty ;\, - 1} \right) \cup \left( {3;\, + \infty } \right)\).
Hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ;\, - 3} \right)\), \(\left( {1;\, + \infty } \right)\); nghịch biến trên \(\left( { - 3;\,1} \right)\).
Hàm số đồng biến trên \(\left( { - 1;\,3} \right)\), nghịch biến trên mỗi khoảng \(\left( { - \infty ;\, - 1} \right)\), \(\left( {3;\, + \infty } \right)\).
Cho hàm số \(y = \frac{{ - x + 2}}{{x - 1}}\). Khẳng định nào sau đây đúng?
Hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\).
Hàm số nghịch biến trên mỗi khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\).
Hàm số đồng biến trên \(\mathbb{R}\backslash \left\{ 1 \right\}\).
Hàm số đồng biến với mọi \(x \ne 1\).
Hàm số nào sau đây đồng biến trên ?
\[y = {x^2} + 1\].
\(y = \frac{x}{{x + 1}}\).
\(y = x + 1\).
\(y = {x^4} + 1\).
Tìm khoảng đồng biến của hàm số \(y = - {x^3} + 3{x^2} - 1\).
\(\left( {0;2} \right)\).
\(\left( {0;3} \right)\).
\(\left( { - 1;3} \right)\).
\(\left( { - 2;0} \right)\).
Cho hàm số \(y = {x^4} - 8{x^2} + 2019\). Mệnh đề nào sau đây sai?
Hàm số nghịch biến trên khoảng \(\left( { - \infty \,;\,2} \right)\).
Hàm số nghịch biến trên khoảng \(\left( {0\,;\,2} \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - \infty \,;\, - 2} \right)\).
Hàm số đồng biến trên khoảng \(\left( {2\,;\, + \infty } \right)\).
Cho hàm số \(y = \frac{{x - 1}}{x}\). Mệnh đề nào sau đây là đúng?
Hàm số đã cho chỉ đồng biến trên \(\left( {0; + \infty } \right)\).
Hàm số đã cho chỉ đồng biến trên \(\left( { - \infty ;0} \right)\).
Hàm số đã cho đồng biến trên \(\mathbb{R}\backslash \left\{ 0 \right\}\).
Hàm số đã cho đồng biến trên mỗi khoảng xác định.
Hàm số \(f\left( x \right) = - {x^3} + 3{x^2} + 9x + 1\) đồng biến trong khoảng nào sau đây?
\(\left( {3; + \infty } \right)\)
\(\left( { - 1; + \infty } \right)\)
\(\left( { - 1;3} \right)\).
\(\left( { - \infty ;3} \right)\).
Cho hàm số \[y = \frac{{x - 2}}{{x + 3}}\]. Tìm khẳng định đúng:
Hàm số xác định trên \[\mathbb{R}\backslash \left\{ 3 \right\}\].
Hàm số đồng biến trên \[\mathbb{R}\backslash \left\{ { - 3} \right\}\].
Hàm số nghịch biến trên mỗi khoảng xác định.
Hàm số đồng biến trên mỗi khoảng xác định.
Hàm số nào sau đây đồng biến trên \(\mathbb{R}\)?
\(y = {x^4} - {x^3} + 2x\).
\(y = \sin x\).
\(y = \frac{{x - 1}}{{x + 1}}\).
\(y = x\sqrt {{x^2} + 1} \).
Cho hàm số \(y = {x^3} + 3x + 2\). Mệnh đề nào dưới đây là đúng ?
Hàm số đồng biến trên khoảng \(\left( { - \infty ; + \infty } \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - \infty ; + \infty } \right)\).
Hàm số đồng biến trên khoảng \(\left( { - \infty ;0} \right)\) và nghịch biến trên khoảng \(\left( {0; + \infty } \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\).
Cho hàm số \(y = {x^3} -6{x^2} + 12x + 1\). Khẳng định nào sau đây là đúng?
Hàm số đồng biến trên \(\mathbb{R}\).
Hàm số nghịch biến \(\mathbb{R}\).
Hàm số đồng biến trên khoảng \(\left( { - \infty ;2} \right)\) và nghịch biến trên khoảng \(\left( {2; + \infty } \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - \infty ;2} \right)\) và đồng biến trên khoảng \(\left( {2; + \infty } \right)\).
Hàm số \(y = {x^4} + 2{x^2} - 1\)đồng biến trên khoảng nào sau đây?
\(( - 1\,;\,1)\).
\((0\,;\, + \infty )\).
\(\mathbb{R}\).
\(( - \infty \,;\,0)\).
Trong các hàm số sau, hàm số nào luôn đồng biến trên \(\mathbb{R}\) ?
\(y = {x^3} - {x^2} + x + 4\).
\(y = \frac{{2x - 5}}{{x + 2}}\).
\(y = {x^4} + 3{x^2} - 4\).
\[y = {x^2} - 2x - 2\].
Tìm khoảng đồng biến của hàm số: \(y = {x^4} - 6{x^2} + 8x + 1\).
\(\left( { - \infty ;1} \right)\).
\(\left( { - 2; + \infty } \right)\).
\(\left( { - \infty ; + \infty } \right)\).
\(\left( { - \infty ;2} \right)\).
Cho hàm số \[y = \frac{{x - 2}}{{x + 3}}\]. Mệnh đề nào sau đây đúng?
Hàm số nghịch biến trên khoảng \(\left( { - \infty ; + {\infty ^{}}} \right)\).
Hàm số nghịch biến trên từng khoảng xác định.
Hàm số đồng biến trên từng khoảng xác định.
Hàm số đồng biến trên khoảng \(\left( { - \infty ; + {\infty ^{}}} \right)\).
Cho hàm số \(y = \frac{{2x + 1}}{{x + 1}}\). Mệnh đề đúng là
Hàm số nghịch biến trên các khoảng \(\left( { - \infty \,;\, - 1} \right)\) và \(\left( { - 1\,;\, + \infty } \right)\)
Hàm số nghịch biến trên \(\left( -\infty;\, -1 \right) \cup \left( -1;\, +\infty \right)\).
Hàm số đồng biến trên tập \(\mathbb{R}\).
Hàm số đồng biến trên các khoảng \(\left( { - \infty \,;\, - 1} \right)\) và \(\left( { - 1\,;\, + \infty } \right)\).
Hàm số \[y = - {x^3} + 3x - 4\]đồng biến trên khoảng nào dưới đây?
\[\left( { - \infty ; - 1} \right)\].
\[\left( { - \infty ; - 1} \right)\]và \[\left( {1; + \infty } \right)\].
\[\left( {1; + \infty } \right)\].
\[\left( { - 1;1} \right)\].
Trong các hàm số sau, hàm số nào luôn nghịch biến trên \(\mathbb{R}\)?
\(y = - x + 4\).
\(y = - {x^3} + 3{x^2}\).
\[y = \frac{{2x + 3}}{{x + 1}}\].
\[y = {x^4} - 3{x^2} - 1\].
Trong các hàm số sau, hàm số nào đồng biến trên tập xác định của nó?
\(y = \frac{{2x - 1}}{{x + 2}}\).
\(y = {x^3} + 4x + 1\).
\(y = {x^2} + 1\).
\(y = {x^4} + 2{x^2} + 1\).
Hàm số \[y = {x^4} - 2\] nghịch biến trên khoảng nào?
\[\left( { - \infty ;\frac{1}{2}} \right)\].
\[\left( { - \infty ;0} \right)\].
\[\left( {\frac{1}{2}; + \infty } \right)\].
\[\left( {0; + \infty } \right).\]
Cho hàm số \(y = {x^3} + 3x + 2\). Mệnh đề nào dưới đây là đúng?
Hàm số đồng biến trên khoảng \(\left( { - \infty ; + \infty } \right)\)
Hàm số nghịch biến trên khoảng \(\left( { - \infty ; + \infty } \right)\)
Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\)
Hàm số đồng biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\)
Cho hàm số \(y = \frac{{x + 1}}{{1 - x}}\). Phát biểu nào sau đây đúng?
Hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ;\,1} \right)\) và \(\left( { - 1; + \infty } \right)\).
Hàm số đồng biến trên \(\left( { - \infty ;\,1} \right) \cup \left( {1; + \infty } \right)\).
Hàm số đồng biến trên khoảng \(\left( { - \infty ;\,1} \right)\).
Hàm số đồng biến trên khoảng \(\left( { - 1; + \infty } \right)\).
Cho hàm số \[y = - {x^3} - 3{x^2} + 4\]. Mệnh đề nào dưới đây đúng ?
Hàm số đồng biến trên khoảng \[\left( { - \infty ;\, - 2} \right)\].
Hàm số nghịch biến trên khoảng \[\left( { - 2;\,0} \right)\].
Hàm số đồng biến trên khoảng \[\left( {0;\, + \infty } \right)\].
Hàm số đồng biến trên khoảng \[\left( { - 2;\,0} \right)\].
Cho hàm số \(y = {x^3} + 3{x^2} - 9x + 15\). Khẳng định nào sau đây là sai?
Hàm số đồng biến trên \(( - 9; - 5)\)
Hàm số nghịch biến trên khoảng \(( - 3;1)\).
Hàm số đồng biến trên khoảng \((5; + \infty )\).
Hàm số đồng biến trên \(\mathbb{R}\).
Hàm số \[y = {x^3} - 3x{}^2 + 10\] nghịch biến trên khoảng nào sau đây?
\(\left( {0; + \infty } \right)\).
\(\left( { - \infty ;2} \right)\).
\(\left( { - \infty ;0} \right);\,\,\left( {2; + \infty } \right)\).
\(\left( {0;2} \right)\).
Tìm khoảng đồng biến của hàm số \(y = - {x^3} + 3{x^2} - 1\).
\(\left( {0;2} \right)\).
\(\left( {0;3} \right)\).
\(\left( { - 1;3} \right)\).
\(\left( { - 2;0} \right)\).
Hàm số \(y = {x^3} - 3x + 5\) đồng biến trong khoảng nào dưới đây?
\(\left( { - 1; + \infty } \right)\).
\(\left( { - \infty ; - 1} \right) \cup \left( {1; + \infty } \right)\).
\(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\).
\(\left( { - \infty ;1} \right)\).
Hàm số \[y = {x^3} - 3x\] nghịch biến trên khoảng nào?
\[\left( { - \infty ;\; - 1} \right)\].
\[\left( { - \infty ;\; + \infty } \right)\].
\[\left( { - 1;\;1} \right)\].
\[\left( {1;\; + \infty } \right)\].
Trong các hàm số sau, hàm số đồng biến trên \(\mathbb{R}\)?
\(y = \frac{{2x - 1}}{{x + 3}}\).
\(y = {x^2} + 2x - 1\).
\(y = 3x + 2\).
\(y = {x^4} - 2{x^2}\).
Cho hàm số \(y = \frac{{2x - 1}}{{x + 1}}\). Kết luận nào sau đây đúng?
Hàm số đồng biến trên \(\mathbb{R}\).
Hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ; - 1} \right);\left( { - 1; + \infty } \right)\).
Hàm số nghịch biến trên \(\mathbb{R}\).
Hàm số nghịch biến trên mỗi khoảng \(\left( { - \infty ; - 1} \right);\left( { - 1; + \infty } \right)\).
Hàm số \(y = \frac{{2x - 1}}{{x + 1}}\) đồng biến trên khoảng nào dưới đây?
\(\left( {1;4} \right)\).
\(\left( { - 2; + \infty } \right)\).
\(\left( { - \infty ;0} \right)\).
\(\left( { - \infty ; + \infty } \right)\).
Hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} - 1\)đồng biến trên miền nào dưới đây?
\(\left( {0;4} \right).\)
\(\left( {1; + \infty } \right).\)
\(\left( { - \infty ;0} \right).\)
\(\left( { - \infty ;0} \right) \cup \left( {2; + \infty } \right).\)
Cho hàm số . Mệnh đề nào dưới đây đúng?
Hàm số đồng biến trên khoảng .
Hàm số nghịch biến trên khoảng .
Hàm số đồng biến trên khoảng .
Hàm số đồng biến trên .
Cho các hàm số \(y = \frac{{x + 1}}{{x + 2}}\), \(y = \tan x\), \(y = {x^3} + {x^2} + 4x - 2017\). Số hàm số đồng biến trên (\mathbb{R}\)là
0.
3.
1.
2.
Trong các hàm số sau, hàm số nào đồng biến trên tập xác định của nó?
\(y = \frac{{2x - 1}}{{x + 2}}\).
\(y = {x^3} + 4x + 1\).
\(y = {x^2} + 1\).
\(y = \frac{{{x^2} + 2x + 3}}{{x - 1}}\).
Hàm số nào sau đây đồng biến trên khoảng \(\left( { - \infty ; + \infty } \right)\)?
\(y = \frac{{x - 1}}{{x + 3}}\).
\(y = - {x^3} - 3x\).
\(y = \frac{{{x^2} - x - 1}}{{x - 2}}\).
\(y = {x^3} + x\).
Hàm số \(y = \frac{x}{{{x^2} + 1}}\) đồng biến trên khoảng
\(\left( { - 1;1} \right)\).
\(\left( {0; + \infty } \right)\).
\(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\).
\(\left( { - \infty ; + \infty } \right)\).
Hàm số nào dưới đây đồng biến trên \(\mathbb{R}\)?
\(y = \sqrt {x + 1} \).
\(y = {x^3} + x - 2\).
\(y = \frac{{ - {x^2} + 2x + 3}}{{x + 4}}\).
\(y = \frac{{x - 1}}{{x + 1}}\).
Hàm số nào sau đây nghịch biến trên \(\mathbb{R}\)?
\(y = \frac{{2x - 1}}{{x + 2021}}\).
\(y = {x^4} - 2{x^2} - 2021\).
\(y = - {x^3} + {x^2} - x\).
\(y = {x^3} + 2x + 2021\).
Hàm số nào sau đây đồng biến trên \[\mathbb{R}\]?
\[y = 2x - \cos 2x - 5\].
\[y = \frac{{2x - 1}}{{x + 1}}\].
\[y = {x^2} - 2x\].
\[y = \sqrt x \].
Hàm số \(f\left( x \right) = {\left( {{x^2} + 3x + 2} \right)^2}\) nghịch biến trong khoảng nào dưới đây?
\[\left( { - \frac{3}{2}; - 1} \right)\].
\[\left( { - 2; - 1} \right)\].
\[\left( { - 2; - \frac{3}{2}} \right)\].
\[\left( { - 1;1} \right)\].
Hàm số \(y = \sqrt {x - {x^2}} \) nghịch biến trên khoảng
\((\frac{1}{2};\,1)\).
\((0;\,\frac{1}{2})\).
\(( - \infty ;\,0)\).
\((1;\, + \infty )\).
Hàm số \(f\left( x \right)\) có \(f'\left( x \right) = \left( {x - 1} \right)\left( {x - 2} \right),\forall x \in \mathbb{R}\) nghịch biến trên khoảng nào dưới đây?
\(\left( { - 2; - 1} \right)\).
\(\left( {1;2} \right)\).
\(\left( {2; + \infty } \right)\).
\(\left( { - \infty ; - 1} \right)\).
Cho hàm số \[y = f\left( x \right)\] có đạo hàm \[f'\left( x \right) = {x^2} + 1\], \[\forall x \in \mathbb{R}\]. Mệnh đề nào dưới đây đúng?
Hàm số nghịch biến trên khoảng \[\left( { - \infty ;0} \right)\]
Hàm số nghịch biến trên khoảng \[\left( {1; + \infty } \right)\]
Hàm số nghịch biến trên khoảng \[\left( { - 1;1} \right)\]
Hàm số đồng biến trên khoảng \[\left( { - \infty ; + \infty } \right)\]
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = {\left( {x + 1} \right)^2}{\left( {x - 1} \right)^3}\left( {2 - x} \right)\). Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
\(\left( {1;2} \right)\).
\(\left( { - \infty ; - 1} \right)\).
\(\left( { - 1;1} \right)\).
\(\left( {2; + \infty } \right)\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {x^2} + 1\). Khẳng định nào sau đây đúng ?
Hàm số đồng biến trên \(\left( { - \infty ; + \infty } \right)\).
Hàm số nghịch biến trên \(\left( { - \infty ;1} \right)\).
Hàm số nghịch biến trên \(\left( { - \infty ; + \infty } \right)\).
Hàm số nghịch biến trên \(\left( { - 1;1} \right)\).
Cho hàm số \(y = f\left( x \right)\)có đạo hàm \(f'\left( x \right) = x{\left( {x - 2} \right)^3}\), với mọi \(x \in \mathbb{R}\). Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
\(\left( {1;\,\,3} \right)\).
\(\left( { - 1;\,\,0} \right)\).
\(\left( {0;\,\,1} \right)\).
\(\left( { - 2;\,\,0} \right)\).
Cho hàm số \[y = f\left( x \right)\] có đạp hàm \[f'\left( x \right) = {x^2} + 1\], \[\forall x \in \mathbb{R}\]. Mệnh đề nào dưới đây đúng ?
Hàm số nghịch biến trên khoảng \[\left( { - \infty ;0} \right)\].
Hàm số nghịch biến trên khoảng \[\left( {1; + \infty } \right)\].
Hàm số nghịch biến trên khoảng \[\left( { - 1;1} \right)\].
Hàm số đồng biến trên khoảng \[\left( { - \infty ; + \infty } \right)\].
Cho hàm số \(y = f\left( x \right)\)có \(f'\left( x \right) = \left( {x + 2} \right)\left( {x + 1} \right)\left( {{x^2} - 1} \right)\). Hàm số \(y = f\left( x \right)\)đồng biến trên khoảng nào sau đây?
\(\left( { - 1;1} \right)\).
\(\left( {0; + \infty } \right)\).
\(\left( { - \infty ; - 2} \right)\).
\(\left( { - 2; - 1} \right)\).
Cho hàm số \(y = f\left( x \right)\)liên tục trên \(\mathbb{R}\)và có đạo hàm \(f'\left( x \right) = {\left( {x + 1} \right)^2}{\left( {x - 1} \right)^3}\left( {2 - x} \right)\). Hàm số \(y = f\left( x \right)\)đồng biến trên khoảng nào dưới đây?
\(\left( {1\,;\,2} \right)\).
\(\left( { - \infty \,;\, - 1} \right)\).
\[\left( { - 1\,;\,1} \right)\].
\(\left( {2\,;\, + \infty } \right)\).
Cho hàm số \[y = f\left( x \right)\] có đạo hàm \[f'\left( x \right) = {\left( {x + 1} \right)^2}\left( {2 - x} \right)\left( {x + 3} \right)\]. Mệnh đề nào dưới đây đúng?
Hàm số nghịch biến trên khoảng \[\left( { - 3;2} \right)\].
Hàm số nghịch biến trên các khoảng \[\left( { - 3; - 1} \right)\] và \[\left( {2; + \infty } \right)\].
Hàm số đồng biến trên các khoảng \[\left( { - \infty ; - 3} \right)\] và \[\left( {2; + \infty } \right)\].
Hàm số đồng biến trên khoảng \[\left( { - 3;2} \right)\].
Cho hàm số \(y = f\left( x \right)\) có \(f'\left( x \right) = {x^2} - 4x\) với mọi \(x\) là số thực. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
\(\left( {2; + \infty } \right)\).
\(\left( { - 1;0} \right)\).
\(\left( {0;4} \right)\).
\(\left( { - 2;1} \right)\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = {\left( {x + 1} \right)^2}{\left( {x - 1} \right)^3}\left( {2 - x} \right)\). Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
\(\left( { - \infty ;\, - 1} \right)\).
\(\left( { - 1;\,1} \right)\).
\(\left( {2;\, + \infty } \right)\).
\(\left( {1;\,2} \right)\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên tập \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = \left( {x - 1} \right){\left( {x + 1} \right)^2}\left( {x - 3} \right)\). Tìm các khoảng đồng biến của hàm số \(f\left( x \right)\).
\(\left( { - \infty ;1} \right)\) và \(\left( {3; + \infty } \right)\).
\(\left( { - 1;1} \right)\) và \(\left( {3; + \infty } \right)\).
\(\left( {1;3} \right)\).
\(\mathbb{R}\).
Cho hàm số \(f\left( x \right)\)có đạo hàm là \(f'\left( x \right) = x{\left( {x + 1} \right)^2}\). Hàm số đồng biến trên khoảng nào dưới đây?
\(\left( { - 1; + \infty } \right)\).
\(\left( { - 1;0} \right)\).
\(\left( { - \infty ; - 1} \right)\).
\(\left( {0; + \infty } \right)\).
Cho hàm số \(y = f\left( x \right)\)có đạo hàm \(y = f'\left( x \right) = x\left( {x - 2} \right),\,\forall x \in \mathbb{R}\). Hàm số \(y = f\left( x \right)\)nghịch biến trên khoảng nào dưới đây?
\(\left( {2; + \infty } \right)\).
\(\left( {0; + \infty } \right)\).
\(\left( { - \infty ;0} \right)\).
\(\left( {0;2} \right)\).
Cho \(f'\left( x \right) = x{\left( {1 - x} \right)^2}{\left( {x - 2} \right)^3}\). Hàm số \(y = f(x)\) nghịch biến trên khoảng nào sau đây?
\(\left( {1;2} \right)\).
\(\left( {1; + \infty } \right)\).
\(\left( { - \infty ;0} \right)\).
\(\left( { - 1;1} \right)\).
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = {\left( {x + 1} \right)^2}{\left( {x - 1} \right)^3}\left( {2 - x} \right)\). Hàm số \(y = f\left( x \right)\)đồng biến trên khoảng nào dưới đây?
\[\left( { - 1;1} \right)\].
\[\left( {2; + \infty } \right)\].
\[\left( {1;2} \right)\].
\[\left( { - \infty ; - 1} \right)\].
Cho hàm số \[y = f\left( x \right)\] có đạo hàm \[f'\left( x \right) = {\left( {x + 1} \right)^2}\left( {2 - x} \right)\left( {x + 3} \right)\]. Mệnh đề nào dưới đây đúng?
Hàm số nghịch biến trên khoảng \[\left( { - 3;2} \right)\].
Hàm số nghịch biến trên các khoảng \[\left( { - 3; - 1} \right)\] và \[\left( {2; + \infty } \right)\].
Hàm số đồng biến trên các khoảng \[\left( { - \infty ; - 3} \right)\] và \[\left( {2; + \infty } \right)\].
Hàm số đồng biến trên khoảng \[\left( { - 3;2} \right)\].
Cho hàm số \(y = f\left( x \right)\)có đồ thị như hình bên
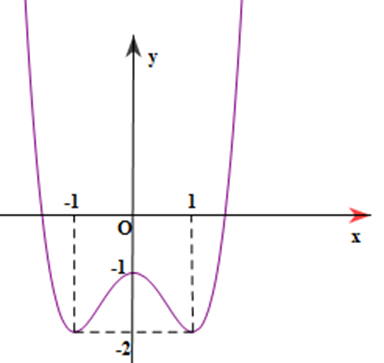
Hàm số đã cho đồng biền trên khoảng nào dưới đây?
\[\left( {0;1} \right)\].
\[\left( { - \infty ; - 1} \right)\].
\[\left( { - 1;1} \right)\].
\[\left( { - 1;0} \right)\].
Cho hàm số \(y = f\left( x \right)\)có đồ thị như hình vẽ
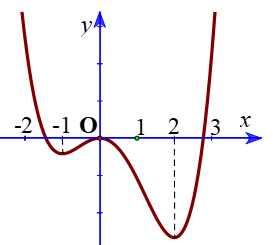
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
\(\left( { - 2; - 1} \right)\).
\(\left( {0;1} \right)\).
\(\left( {1;2} \right)\).
\(\left( { - 1;0} \right)\).
Cho hàm số \[y = f(x)\] có đồ thị như hình vẽ.
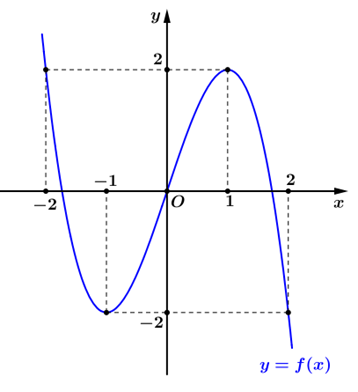
Hàm số \[y = f(x)\] đồng biến trong khoảng nào trong các khoảng sau đây?
\(( - \infty ;2)\).
\(( - 1;1)\).
\((0;2)\).
\((1; + \infty )\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào trong các khoảng dưới đây?
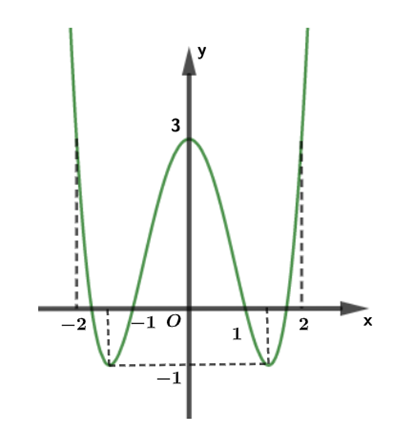
\(\left( {0;1} \right).\)
\(\left( { - 2; - 1} \right).\)
\(\left( { - 1;0} \right).\)
\(\left( { - 1;3} \right).\)
Cho hàm số \[f\left( x \right)\]liên tục trên \[\mathbb{R}\]và có đồ thị như hình vẽ dưới đây, hàm số \[f\left( x \right)\]đồng biến trên khoảng nào?
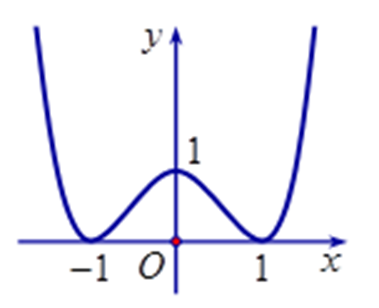
\[\left( { - \infty ;0} \right)\].
\[\left( { - \infty ; - 1} \right)\].
\(\left( {1; + \infty } \right)\).
\(\left( { - 1;1} \right)\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
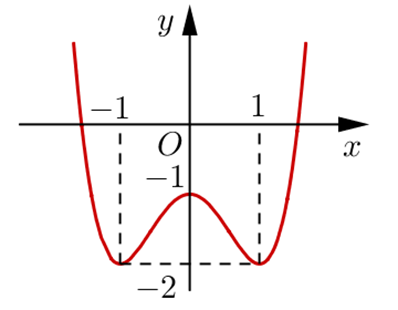
\(\left( {0;1} \right)\).
\(\left( {1; + \infty } \right)\).
\(\left( { - 1;1} \right)\).
\(\left( { - 1;0} \right)\).
Đường cong trong hình vẽ bên là đồ thị của hàm số có dạng \(y = a{x^3} + b{x^2} + cx + d\,\,\left( {a \ne 0} \right)\).
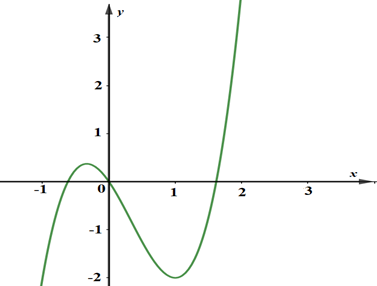
Hàm số nghịch biến trong khoảng nào dưới đây?
\(\left( { - \infty ;\,\, - 2} \right)\).
\(\left( {1;\,\,2} \right)\).
\(\left( {0;\,\,\frac{1}{2}} \right)\).
\(\left( {0;\,\,3} \right)\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên dưới. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
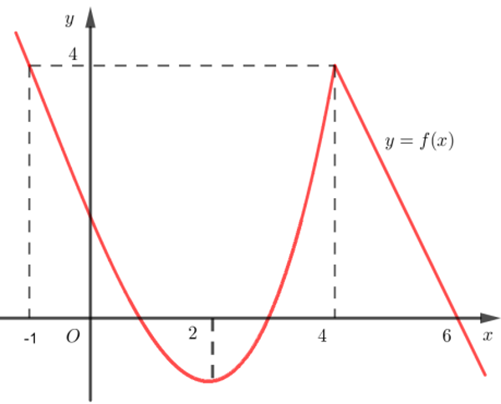
\[(2;6)\].
\[(0;4)\].
\[(3;4)\].
\[( - 1;4)\].
Cho hàm số \[y = f\left( x \right)\] có đồ thị như sau
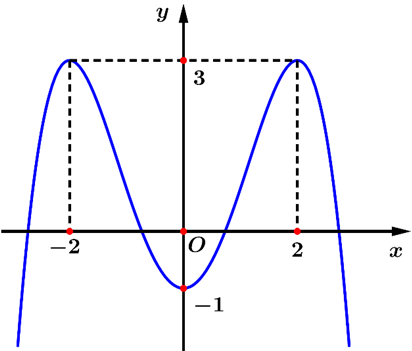
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
\[\left( {0; + \infty } \right)\].
\[\left( { - \infty ; - 2} \right)\].
\[\left( { - 2;0} \right)\].
\[\left( { - 2;2} \right)\].
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên dưới. Hàm số \(y = f\left( x \right)\)đồng biến trên khoảng nào sau đây?
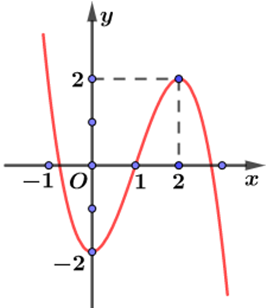
\(\left( {2; + \infty } \right)\).
\(\left( {0;2} \right)\).
\(\left( { - 2;2} \right)\).
\(\left( { - \infty ;0} \right)\).
Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị trong hình bên:
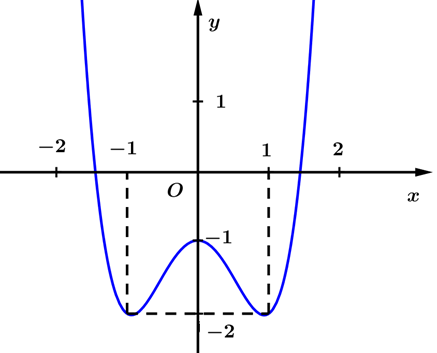
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
\(\left( { - 1;1} \right)\).
\(\left( {0;1} \right)\).
\(\left( {1; + \infty } \right)\).
\(\left( { - 1; + \infty } \right)\).
Cho hàm số \[y = f(x)\] có đồ thị như hình vẽ.
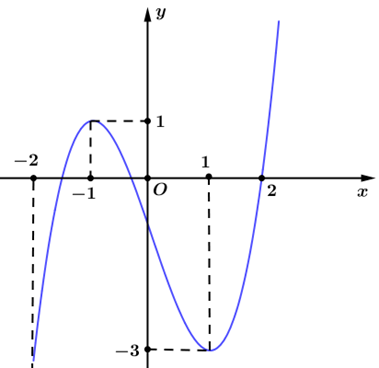
Hàm số \[y = f(x)\] đồng biến trên khoảng nào dưới đây?
\(( - 1;1)\).
\((0;2)\).
\(( - 2; - 1)\).
\(( - 2;1)\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình. Hàm số đã cho đồng biến trên khoảng nào?
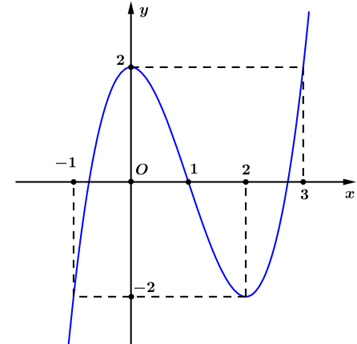
\(\left( {0;1} \right)\).
\(\left( { - \infty ;1} \right)\).
\(\left( { - 1;1} \right)\).
\(\left( { - 1;0} \right)\).
Cho hàm số bậc ba có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng?
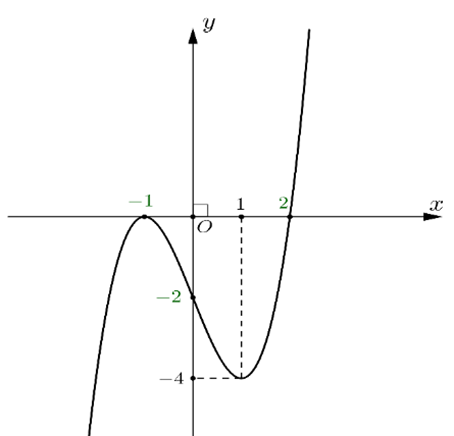
Hàm số nghịch biến trên \(\left( {1; + \infty } \right)\).
Hàm số đồng biến trên \(\left( {1; + \infty } \right)\).
Hàm số nghịch biến trên \(\left( { - \infty ; - 1} \right)\).
Hàm số đồng biến trên \(\left( { - 1;1} \right)\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
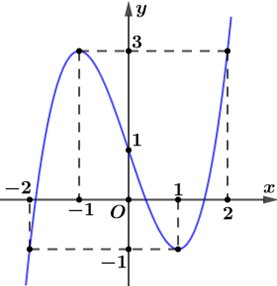
\[\left( { - 1\,;\, + \infty } \right).\]
\[\left( { - 1\,;\,1} \right).\]
\[\left( { - \infty \,;\,1} \right).\]
\[\left( { - \infty \,;\, - 1} \right).\]
Cho hàm số\[f(x)\] có đồ thị như hình bên, hàm số đồng biến trên khoảng nào trong các phương án dưới đây?
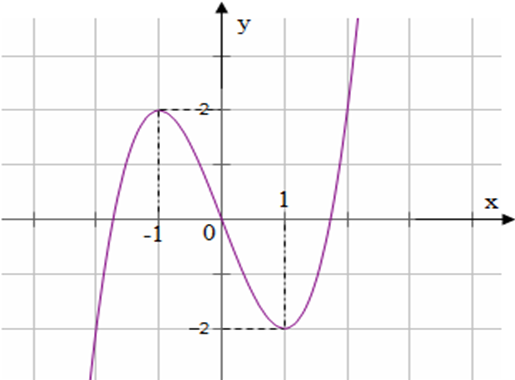
\[\left( { - \infty ;\, - 1} \right)\]và \[\left( {1; + \infty } \right).\]
\[\left( { - 1;\,1} \right)\].
\[\left( { - \infty ;\,2} \right)\].
\[\left( { - 2;\,2} \right)\].
Hàm số \[y = f\left( x \right)\]có đồ thị như hình vẽ.
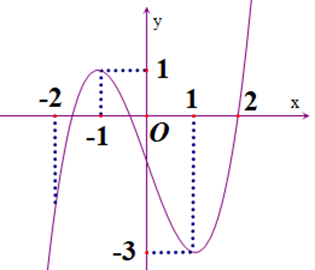
Hàm số \[y = f\left( x \right)\]đồng biến trên khoảng nào dưới đây?
\[\left( { - 1;1} \right)\].
\[\left( {0;2} \right)\].
\[\left( { - 2; - 1} \right)\].
\[\left( { - 2;1} \right)\].
Cho hàm số \(y = f\left( x \right)\)có đồ thị như hình vẽ. Hàm số \(y = f\left( x \right)\)đồng biến trên khoảng nào dưới đây?
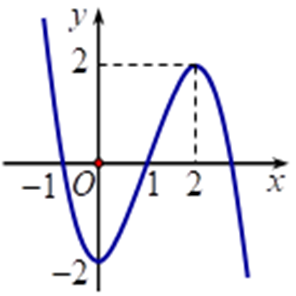
\(\left( {2; + \infty } \right)\).
\(\left( { - 2;2} \right)\).
\(\left( { - \infty ;0} \right)\).
\(\left( {0;2} \right)\).
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình bên, mệnh đề nào sau đây đúng?
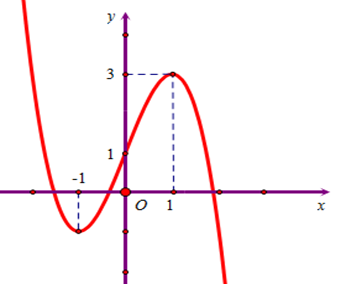
Hàm số nghịch biến trên khoảng \[\left( { - \infty ;0} \right)\].
Hàm số đồng biến trên khoảng \[\left( { - 1;1} \right)\].
Hàm số đồng biến trên khoảng \[\left( { - 1;3} \right)\].
Hàm số nghịch biến trên khoảng \[\left( {0; + \infty } \right)\].
Cho hàm số \[f\left( x \right)\] có đạo hàm liên tục trên \[\mathbb{R}\] và có đồ thị của hàm \[y = f'\left( x \right)\] như hình vẽ. Mệnh đề nào dưới đây sai?
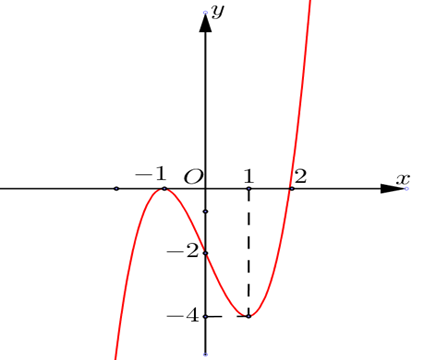
Hàm số \[f\left( x \right)\] nghịch biến trên \(\left( { - 1;0} \right)\).
Hàm số \[f\left( x \right)\] đồng biến trên \(\left( {1; + \infty } \right)\).
Hàm số\[f\left( x \right)\] nghịch biến trên \(\left( { - \infty ;2} \right)\).
Hàm số \[f\left( x \right)\] đồng biến trên \(\left( {2; + \infty } \right)\).
Cho hàm số \(f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) là hàm số \(f'\left( x \right)\). Biết đồ thị hàm số \(f'\left( x \right)\) được cho như hình vẽ. Hàm số \(f\left( x \right)\) nghịch biến trên khoảng
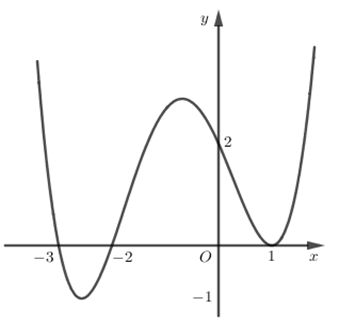
\(\left( {0\,;\,1} \right)\).
\(\left( { - \infty \,;\, - 3} \right)\).
\(\left( { - \infty \,;\, - 1} \right)\).
\(\left( { - 3\,;\, - 2} \right)\).
Cho hàm số \[y = f(x)\]. Hàm số \[y = f'(x)\] có đồ thị như hình bên. Hàm số \[y = f(x)\] đồng biến trên khoảng
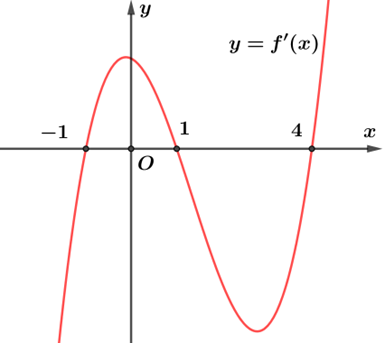
\(( - 1;1)\).
\((1;4)\).
\(( - \infty ; - 1)\).
\((2; + \infty )\).
Cho hàm số \(y = f\left( x \right)\)có đồ thị \(f'\left( x \right)\)là đường cong như hình vẽ bên. Tìm khẳng định đúng.
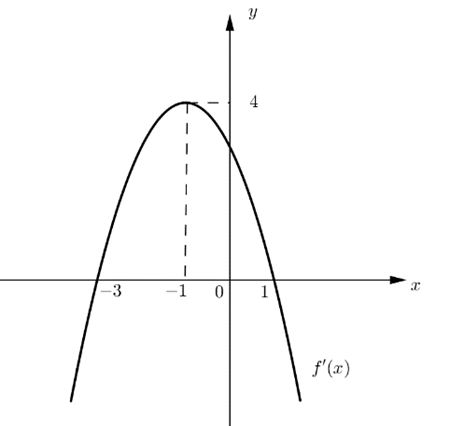
\(f\left( x \right)\)đồng biến trên \(\left( { - 2;\,0} \right)\).
\(f\left( x \right)\)nghịch biến trên \(\left( {0;\, + \infty } \right)\).
\(f\left( x \right)\)đồng biến trên \(\left( { - \infty ;\,3} \right)\).
\(f\left( x \right)\)nghịch biến trên \(\left( { - 3;\, - 2} \right)\).
Cho hàm bậc ba \(y = f\left( x \right)\) có đồ thị đạo hàm \(y = f'\left( x \right)\) như hình bên dưới. Hàm số đã cho nghịch biến trên khoảng
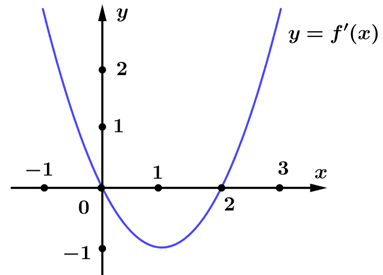
\(\left( {1\,\,;\,\,2} \right)\).
\(\left( { - 1\,\,;\,\,0} \right)\).
\(\left( {3\,\,;\,\,4} \right)\).
\(\left( {2\,\,;\,\,3} \right)\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ bên. Khẳng định nào sau đây đúng về hàm số \(y = f\left( x \right)\)?
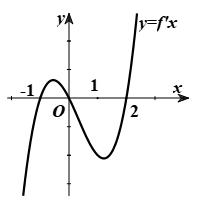
Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 1} \right)\).
Hàm số đồng biến trên khoảng \(\left( { - 1;0} \right)\).
Hàm số đồng biến trên khoảng \(\left( {1;2} \right)\).
Hàm số nghịch biến trên khoảng \(\left( {0; + \infty } \right)\).
Cho hàm số \[y = f(x)\] có đạo hàm trên \[\mathbb{R}\] và đồ thị của hàm số \[y = f'(x)\] như hình vẽ. Hàm số \[y = f(x)\] đồng biến trên khoảng nào sau đây.
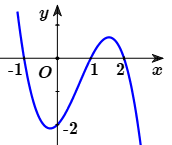
\[(0;1)\].
\[(2; + \infty )\].
\[(1;2)\].
\[( - 1;2)\].
Cho hàm số \(y = f\left( x \right)\) có đồ thị \(y = f'\left( x \right)\) là parabol như hình vẽ.
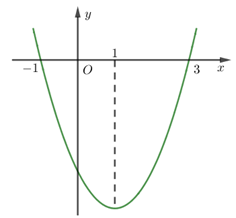
Khẳng định nào sau đây là đúng?
Hàm số đồng biến trên \(\left( {1; + \infty } \right)\).
Hàm số đồng biến trên \(\left( { - \infty ; - 1} \right)\) và \(\left( {3; + \infty } \right)\).
Hàm số nghịch biến trên \(\left( { - \infty ;1} \right)\).
Hàm số đồng biến trên \(\left( { - 1;3} \right)\).
Cho hàm bậc ba \(y = f\left( x \right)\) có đồ thị đạo hàm \(y = f'\left( x \right)\) như hình sau:
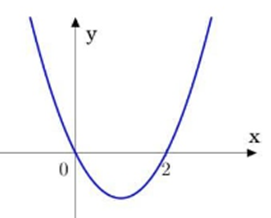
Hàm số đã cho nghịch biến trên khoảng
\(\left( { - 1;0} \right)\) .
\(\left( {2;3} \right)\).
\(\left( {3;4} \right)\).
\(\left( {1;2} \right)\).
Cho hàm số \[y = f(x)\]. Hàm số \[y = f'(x)\] có đồ thị như hình bên. Hàm số \[y = f(x)\] đồng biến trên khoảng
![Cho hàm số y = f(x). Hàm số y = f'(x) có đồ thị như hình bên. Hàm số \[y = f(x)\] đồng biến trên khoảng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/07/blobid29-1753118813.png)
\(( - 1;1)\).
\((1;4)\).
\(( - \infty ; - 1)\).
\((2; + \infty )\).
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có đồ thị hàm số \[f'\left( x \right)\] là đường cong trong hình bên. Mệnh đề nào dưới đây đúng?
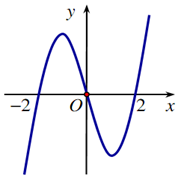
Hàm số \(f\left( x \right)\) nghịch biến trên khoảng\[\left( { - 1;1} \right).\]
Hàm số \(f\left( x \right)\) đồng biến trên khoảng \[\left( {1;{\rm{ }}2} \right).\]
Hàm số \(f\left( x \right)\) đồng biến trên khoảng \[\left( { - 2;1} \right).\]
Hàm số \(f\left( x \right)\) nghịch biến trên khoảng \[\left( {0;{\rm{ }}2} \right).\]
Đường cong ở hình bên là đồ thị của hàm số \(y = \frac{{ax + b}}{{cx + d}}\) với \(a,b,c,d\) là các số thực. Mệnh đề nào dưới đây đúng?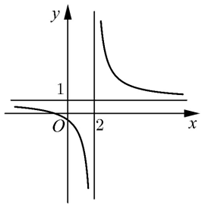
\(y' < 0,\forall x \ne 1\)
\(y' < 0,\forall x \ne 2\)
\(y' > 0,\forall \ne 2\)
\(y' > 0,\forall x \ne 1\)
Hàm số \(f(x)\)có đạo hàm trên \(\mathbb{R}\)là hàm số \(f'(x)\). Biết đồ thị hàm số \(f'(x)\) được cho như hình vẽ. Hàm số \(f(x)\) nghịch biến trên khoảng

\[\left( {\frac{1}{3};1} \right)\].
\[\left( {0; + \infty } \right)\].
\[\left( { - \infty ;\frac{1}{3}} \right)\].
\[\left( { - \infty ;0} \right)\].
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\), đạo hàm \(f'\left( x \right)\) có đồ thị như hình vẽ dưới đây
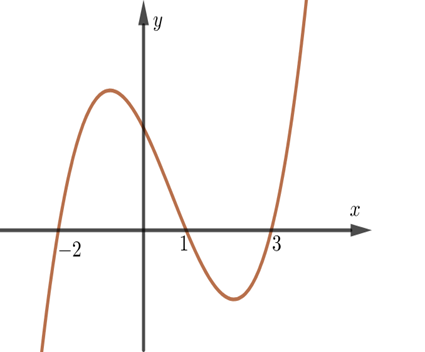
Hãy Chọn khẳng định đúng?
Hàm số đồng biến trên khoảng \(\left( { - 3\,;\, - 2} \right)\).
Hàm số đồng biến trên khoảng \(\left( { - 1\,;\,2} \right)\).
Hàm số nghịch biến trên khoảng \(\left( {1\,;\,3} \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - 1\,;\,1} \right)\).
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(R\) và có đạo hàm \(f'\left( x \right)\). Biết rằng \(f'\left( x \right)\) có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng?
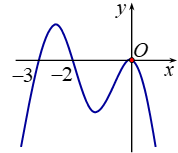
Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( { - 2;0} \right)\).
Hàm số \(y = f\left( x \right)\) NB trên khoảng \(\left( {0; + \infty } \right)\).
Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( { - \,\infty ;3} \right)\).
Hàm số \(y = f\left( x \right)\) NB trên khoảng \(\left( { - 3; - 2} \right)\).
Đường cong ở hình bên là đồ thị của hàm số \(y = \frac{{ax + b}}{{cx + d}}\) với \(a,b,c,d\) là các số thực. Mệnh đề nào dưới đây đúng?
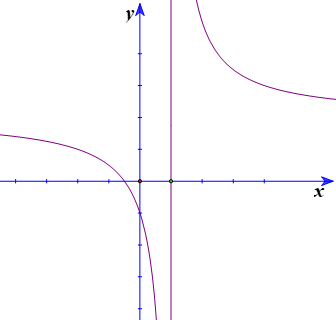
\(y' < 0,\forall x \in \mathbb{R}\).
\(y' > 0,\forall x \ne 1\).
\(y' < 0,\forall x \ne 1\).
\(y' > 0,\forall x \in \mathbb{R}\).
Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\)có đồ thị như hình vẽ:
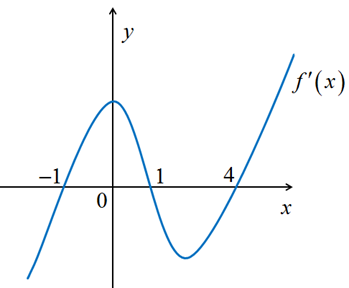
Hàm số \(y = f\left( {1 - {x^2}} \right)\)nghịch biến trên khoảng
\[\left( {0;1} \right)\].
\[\left( {0;2} \right)\].
\[\left( { - \infty ;0} \right)\].
\[\left( {1; + \infty } \right)\].
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ bên dưới.
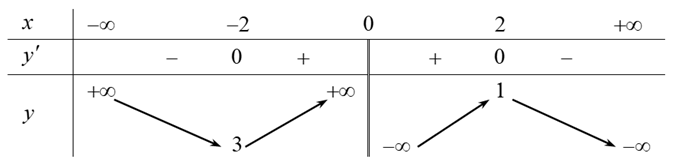
Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
\(\left( { - 2;\,2} \right)\).
\(\left( {0;\,2} \right)\).
\(\left( {3;\, + \infty } \right)\).
\(\left( { - \infty ;\,1} \right)\).
Cho hàm số \(y = f(x)\)có bảng biến thiên như sau:
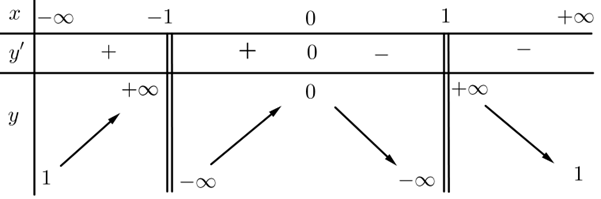
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
\(( - 1;1)\).
\(( - \infty ;0)\).
\(( - 1;0)\).
\((1; + \infty )\).
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
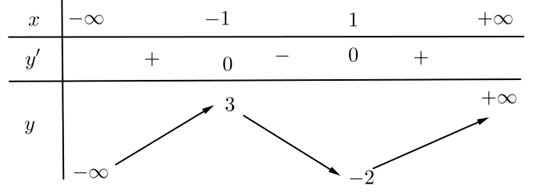
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
\(\left( { - 1;1} \right)\).
\(\left( { - \infty ; - 2} \right)\).
\(\left( { - 2; + \infty } \right)\).
\(\left( { - \infty ;3} \right)\).
Cho hàm số \[y = f\left( x \right)\] xác định và liên tục trên khoảng \[\left( { - \infty ; + \infty } \right),\] có bảng biến thiên như hình sau:
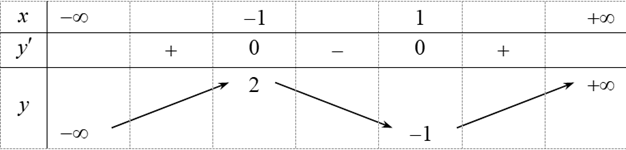
Mệnh đề nào sau đây đúng ?
Hàm số nghịch biến trên khoảng \[\left( {1; + \infty } \right)\].
Hàm số đồng biến trên khoảng \[\left( { - \infty ; - 2} \right)\].
Hàm số nghịch biến trên khoảng \[\left( { - \infty ;1} \right)\].
Hàm số đồng biến trên khoảng \[\left( { - 1; + \infty } \right)\].
Cho hàm số \(y = f\left( x \right)\)có bảng biến thiên sau. Tìm mệnh đề đúng.
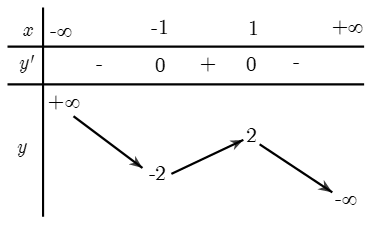
Hàm số \(y = f\left( x \right)\)NB trên khoảng \(\left( { - \infty ;1} \right)\).
Hàm số \(y = f\left( x \right)\)ĐB trên khoảng \(\left( { - 1;1} \right)\).
Hàm số \(y = f\left( x \right)\)ĐB trên khoảng \(\left( { - 2;2} \right)\).
Hàm số \(y = f\left( x \right)\)NB trên khoảng \(\left( { - 1; + \infty } \right)\).
Cho hàm số \[y = f\left( x \right)\] xác định và liên tục trên khoảng \[\left( { - \infty ; + \infty } \right),\] có bảng biến thiên như hình sau:
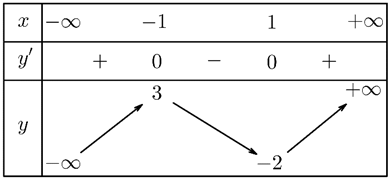
Mệnh đề nào sau đây đúng?
Hàm số nghịch biến trên khoảng \[\left( {1; + \infty } \right)\].
Hàm số đồng biến trên khoảng \[\left( { - \infty ; - 2} \right)\].
Hàm số nghịch biến trên khoảng \[\left( { - \infty ;1} \right)\].
Hàm số đồng biến trên khoảng \[\left( { - 1; + \infty } \right)\].
Cho hàm số \[y = f\left( x \right)\]có bảng biến thiên như sau:
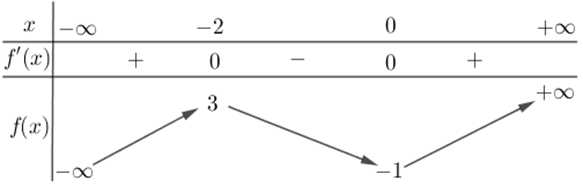
Hàm số đã cho đồng biến trên khoảng nào sau đây?
\[\left( { - 2;0} \right)\].
\[\left( { - \infty ;3} \right)\].
\[\left( { - 1; + \infty } \right)\].
\[\left( { - \infty ; - 2} \right)\].
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ dưới đây. Mệnh đề nào sau đây đúng?
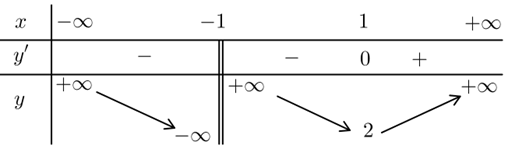
Hàm số nghịch biến trên khoảng \(\left( { - \infty \,;\,1} \right)\).
Hàm số đồng biến trên khoảng \(\left( { - 1\,;\, + \infty } \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - \infty \,;\, - 1} \right) \cup \left( { - 1\,;\,1} \right)\).
Hàm số nghịch biến trên các khoảng \(\left( { - \infty \,;\, - 1} \right)\) và \(\left( { - 1;1} \right)\).
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau:
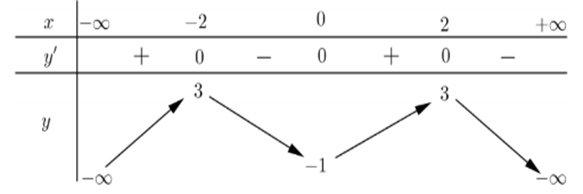
Hàm số \[y = f\left( x \right)\]nghịch biến trên khoảng nào dưới đây?
\[\left( { - 2;0} \right)\]
\[\left( { - \infty ; - 2} \right)\]
\[\left( {0;2} \right)\]
\[\left( {0; + \infty } \right)\]
Cho hàm số \(y = f(x)\) có bảng biến thiên như sau
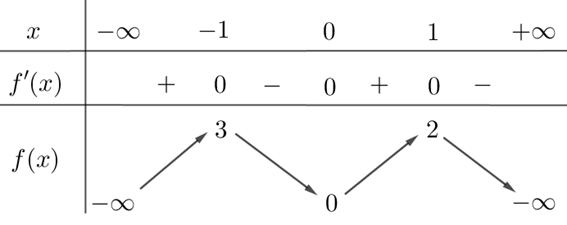
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
\(\left( { - \infty ; - 1} \right)\).
\(\left( {1; + \infty } \right)\).
\(\left( { - \infty ;3} \right)\).
\(\left( {0;2} \right)\).
Cho hàm số \(y = f\left( x \right)\)có đồ thị như như hình vẽ bên dưới. Hàm số \(y = f\left( x \right)\)nghịch biến trên khoảng nào dưới đây?
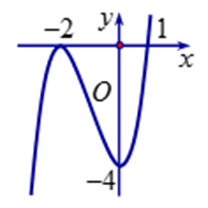
\(\left( { - 1;\,0} \right)\).
\(\left( {1;\, + \infty } \right)\).
\(\left( { - \infty ;\, - 2} \right)\).
\(\left( { - 2;\,1} \right)\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
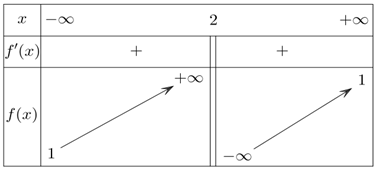
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
\(\left( {1\,;\, + \infty } \right)\).
\(\left( {0\,;\,3} \right)\).
\(\left( { - \infty \,; + \infty } \right)\).
\(\left( {2\,;\, + \infty } \right)\).
Cho hàm số \(AE \bot SD\)có bảng biến thiên như hình vẽ bên. Hàm số \(y = f\left( x \right)\) nghịch biến trên khoảng nào trong các khoảng sau đây?
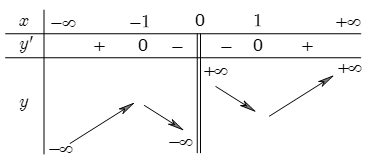
\(\left( { - 1;\,\,0} \right)\).
\(\left( { - 1;\,\,1} \right)\).
\(\left( { - \infty ;\,\, - 1} \right)\).
\[8a + d\].
Cho hàm số \(y = f\left( x \right)\) liên tục trên R và có bảng xét dấu đạo hàm như hình bên. Hàm số \(y = f\left( x \right)\) nghịch biến trên khoảng nào sau đây?

\(\left( { - 2;1} \right)\).
\(\left( {1;3} \right)\).
\(\left( { - \infty ; - 2} \right)\).
\(\left( {3; + \infty } \right)\).
Cho hàm số \[y = f\left( x \right)\] có bảng xét dấu của đạo hàm như sau

Hàm số \[y = - f\left( x \right)\] đồng biến trên khoảng nào dưới đây?
\[\left( {2;3} \right)\].
\[\left( {4; + \infty } \right)\].
\[\left( { - 2; - 1} \right)\].
\[\left( { - 1;3} \right)\].
Cho hàm số \(y = f\left( x \right)\) xác định \(\mathbb{R}\backslash \left\{ 0 \right\}\), liên tục trên từng khoảng xác định và có bảng biến thiên như hình vẽ:

Khẳng định nào sau đây là đúng?
Hàm số nghịch biến trên \(\left( {0;1} \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - 1;1} \right)\).
Hàm số đồng biến trên khoảng \(\left( { - 1;0} \right)\).
Hàm số đồng biến trên \(\left( { - 1; + \infty } \right)\).
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau:
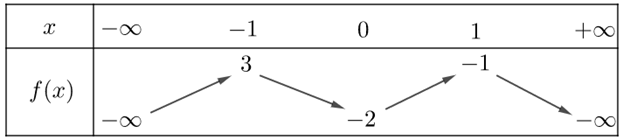
Hàm số \[g\left( x \right) = f\left( {2x + 7} \right)\] nghịch biến trên khoảng nào dưới đây?
\[\left( { - 5; - 4} \right)\].
\[\left( { - 3;0} \right)\].
\[\left( { - 4; - 3} \right)\].
\[\left( { - \infty ; - 5} \right)\].
Cho hàm số \(f(x)\), bảng xét dấu của \(f'(x)\) như sau:
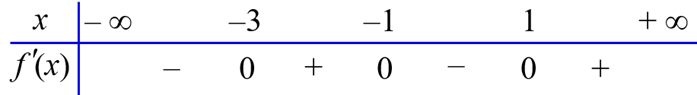
Hàm số \(y = f(1 - 2x)\) nghịch biến trên khoảng nào dưới đây?
\(\left( {1;3} \right)\).
\(\left( {3; + \infty } \right)\).
\(\left( { - 2;0} \right)\).
\(\left( {0;1} \right)\).
Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\,\left( {a \ne 0} \right)\) có bảng biến thiên như sau

Hàm số \(y = f\left( {3x - 4} \right)\) nghịch biến trong khoảng nào?
\(\left( {0;2} \right)\).
\(\left( {\frac{4}{3};2} \right)\).
\(\left( { - 4;2} \right)\).
\(\left( { - \infty ;0} \right)\).
Cho hàm số \(f\left( x \right)\) có bảng xét dấu của đạo hàm như sau:

Hàm số \(y = f\left( { - 3x} \right)\) nghịch biến trên khoảng nào dưới đây?
\(\left( {1;3} \right)\).
\(\left( { - \frac{1}{3};0} \right)\).
\(\left( { - \frac{2}{3}; - \frac{1}{3}} \right)\).
\(\left( { - \frac{4}{3}; - 1} \right)\).
Cho hàm số \(f\left( x \right)\) có bảng xét dấu đạo hàm như sau

Hàm số \(y = f\left( {1 - 2x} \right)\)đồng biến trên khoảng nào dưới đây ?
\(\left( { - \frac{3}{2}\,;\, - 1} \right)\).
\(\left( { - \infty ; - 1} \right)\).
\(\left( { - 1\,;\,0} \right)\).
\(\left( { - \infty ;\, - 2} \right)\).
Cho hàm số\(y = f\left( x \right)\)có đạo hàm liên tục trên \(\mathbb{R}\), dấu của đạo hàm được cho bởi bảng:
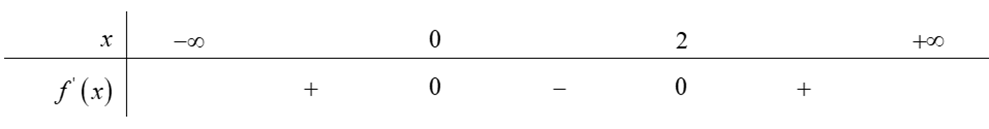
Hàm số \(y = f\left( {2x - 2} \right)\) nghịch biến trong khoảng nào?
\(\left( { - \infty ;1} \right)\).
\(\left( {1;2} \right)\).
\(\left( { - 1;1} \right)\).
\(\left( {2; + \infty } \right)\).
Cho hàm số . Hàm số có đồ thị như hình vẽ.
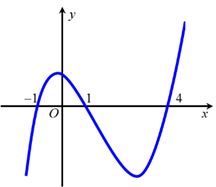
Hàm số đồng biến trên khoảng nào sau đây?
.
.
.
.
Cho hàm số \(y = f\left( x \right)\) có đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ
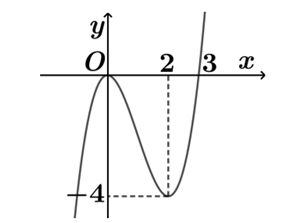
Hàm số \(g\left( x \right) = f\left( {{{\rm{e}}^x} - 2} \right) - 2020\) nghịch biến trên khoảng nào dưới đây?
\(\left( { - 1;\frac{3}{2}} \right)\).
\(\left( { - 1;2} \right)\).
\(\left( {0; + \infty } \right)\).
\(\left( {\frac{3}{2};2} \right)\).
Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\)có đồ thị như hình vẽ.
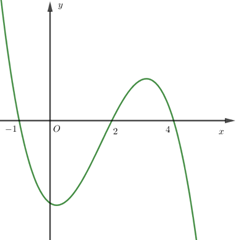
Hàm số \(y = f\left( {10 - {2^x}} \right)\)đồng biến trên khoảng
\(\left( { - \infty ;\,2} \right)\).
\(\left( {2;4} \right)\).
\(\left( {{{\log }_2}6;\,4} \right)\).
\(\left( {{{\log }_2}11;\, + \infty } \right)\).
Cho hàm số \[y = f\left( x \right)\]. Đồ thị hàm số \[y = f'\left( x \right)\] như hình bên. Hàm số \[g\left( x \right) = {\left( {\frac{1}{2}} \right)^{f\left( {1 - 2x} \right)}}\] nghịch biến trên khoảng nào trong các khoảng sau?
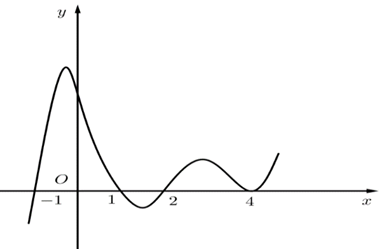
\[\left( {0;1} \right)\].
\[\left( { - \infty ;0} \right)\].
\[\left( { - 1;0} \right)\].
\[\left( {1; + \infty } \right)\].
Hàm số nào dưới đây đồng biến trên tập xác định của nó?
\(y = {\left( {\sqrt 2 } \right)^x}\).
\(y = {\left( {0,5} \right)^x}\).
\(y = {\left( {\frac{{\rm{e}}}{\pi }} \right)^x}\).
\(y = {\left( {\frac{2}{3}} \right)^x}\).
Hàm số nào sau đây nghịch biến trên \[( - \infty ; + \infty )\]?
\[y = {\left( {\frac{3}{\pi }} \right)^{ - x}}\].
\[y = {\left( {1,5} \right)^x}\].
\[y = {\left( {\frac{2}{e}} \right)^x}\].
\[y = {\left( {\sqrt 3 + 1} \right)^x}\].
Hàm số nào dưới đây nghịch biến trên tập xác định của nó?
\[y = {\left( {\frac{{\rm{e}}}{2}} \right)^x}\].
\[y = {\left( {\frac{1}{{\sqrt 6 - \sqrt 5 }}} \right)^x}\].
\[y = {\left( {\frac{4}{{\sqrt 3 + 2}}} \right)^x}\].
\[y = {\left( {\frac{{\pi + 3}}{{2\pi }}} \right)^x}\].
Trong các hàm số sau. Hàm số nào đồng biến trên \(\mathbb{R}\)?
\(y = {\left( {0,9} \right)^x}\).
\(y = {\pi ^x}\).
\(y = {\left( {\frac{2}{\pi }} \right)^x}\).
\(y = {\left( {\frac{1}{3}} \right)^x}\).
Trong các hàm số sau hàm số nào đồng biến trên tập xác định của nó ?
\(y = {\log _{\frac{2}{5}}}x\).
\(y = {\left( {\frac{\pi }{4}} \right)^x}\).
\(y = {\log _{\frac{1}{3}}}\left( {\frac{1}{x}} \right)\).
\(y = {e^{ - x}}\).
Hàm số nào dưới đây đồng biến trên tập xác định của nó?
\(y = {\left( {0,5} \right)^x}\).
\(y = {\left( {\sqrt 2 } \right)^x}\).
\(y = {\left( {\frac{2}{3}} \right)^x}\).
\(y = {\left( {\frac{e}{\pi }} \right)^x}\).
Hàm số nào sau đây đồng biến trên khoảng \(\left( { - \infty ; + \infty } \right)\)?
\(y = {\left( {\frac{e}{4}} \right)^x}\).
\(y = {\left( {\frac{2}{3}} \right)^x}\).
\(y = {\left( {\frac{\pi }{3}} \right)^x}\).
\(y = {\left( {\frac{3}{4}} \right)^x}\).
Hàm số \(y = {\log _{\frac{e}{3}}}\left( {x - 1} \right)\)nghịch biến trên khoảng nào dưới đây?
\(\left( {1; + \infty } \right)\).
\(\left[ {1; + \infty } \right)\).
\(\left( {0; + \infty } \right)\).
\(\mathbb{R}\).
Trong các hàm số sau, hàm số nào nghịch biến trên \[\left( {0; + \infty } \right)\]?
\(y = {\log _{\frac{2}{3}}}x.\)
\(y = {\log _{2020}}x.\)
\(y = {\log _\pi }x\).
\(y = \ln x\).
Hàm số nào sau đây luôn nghịch biến trên \[\mathbb{R}\]?
\(y = - {x^4} + 4{x^2} - 4\).
\(y = - {x^3} - 2x + 3\).
\(y = \frac{{x + 2}}{{x - 1}}\).
\(y = {\log _{\frac{1}{3}}}x\).
Hàm số nào sau đây đồng biến trên tập xác định của nó?
\(y = {\left( {\frac{1}{3}} \right)^x}\).
\(y = {{\rm{e}}^{ - x}}\).
\(y = {\log _{\frac{1}{5}}}x\).
\(y = \ln x\).
Hàm số nào sau đây nghịch biến trên khoảng xác định của nó?
\(y = {\log _{\frac{1}{3}}}x\).
\(y = {\log _{\sqrt 3 }}x\).
\(y = {\log _{\sqrt 2 }}x\).
\(y = {\log _2}x\).
Hàm số nào dưới đây nghịch biến trên tập xác định của nó?
\(y = {\log _2}x\).
\(y = {\log _{\sqrt 3 }}x\).
\(y = {\log _{\frac{e}{\pi }}}x\).
\(y = {\log _\pi }x\).
Trong các hàm số sau hàm số nào đồng biến trên \(\mathbb{R}\).
\(y = {\log _3}x\).
\(y = {\log _{\frac{1}{5}}}x\).
\(y = {\left( {\frac{e}{3}} \right)^x}\).
\(y = {\left( {\frac{2}{3}} \right)^{ - x}}\).
Cho hàm số \(y = {\log _2}\left( {2{x^2} - x - 1} \right)\). Hãy chọn phát biểu đúng.
Hàm số nghịch biến trên \(\left( { - \infty ; - \frac{1}{2}} \right)\), đồng biến trên \(\left( {1; + \infty } \right)\).
Hàm số đồng biến trên \(\left( { - \infty ; - \frac{1}{2}} \right)\) và \(\left( {1; + \infty } \right)\).
Hàm số nghịch biến trên \(\left( { - \infty ; - \frac{1}{2}} \right)\) và \(\left( {1; + \infty } \right)\).
Hàm số đồng biến trên \(\left( { - \infty ; - \frac{1}{2}} \right)\), nghịch biến trên \(\left( {1; + \infty } \right)\).
Cho hàm số \(y = \left( {{x^2} - 3} \right){e^x}\). Chọn mệnh đề đúng trong các mệnh đề sau
Hàm số đồng biến trên khoảng \[\left( { - \infty ;1} \right)\].
Hàm số nghịch biến trên khoảng \[\left( { - 3;1} \right)\].
Hàm số nghịch biến trên khoảng \[\left( {1; + \infty } \right)\].
Hàm số đồng biến trên khoảng \[\left( { - 1;3} \right)\].
Hàm số \(y = {\log _2}\left( {{x^2} - 2x} \right)\) đồng biến trên
\(\left( {1; + \infty } \right)\).
\(\left( {2; + \infty } \right)\).
\(\left( { - 1;1} \right)\).
\(\left( {0; + \infty } \right)\).
Hàm số \(y = {x^2}{{\rm{e}}^{2x}}\) nghịch biến trên khoảng nào?
\(\left( { - \infty ;0} \right)\).
\(\left( { - 2;0} \right)\).
\(\left( {1; + \infty } \right)\).
\(\left( { - 1;0} \right)\).
Hàm số \(y = {\log _{\frac{1}{3}}}\left( {{x^2} - 2x - 3} \right)\) nghịch biến trên khoảng nào trong các khoảng sau đây?
\(\left( { - \infty ;1} \right)\).
\(\left( { - \infty ; - 1} \right)\).
\(\left( {1; + \infty } \right)\).
\(\left( {3; + \infty } \right)\).
Cho hàm số \(y = {e^{2x}} - x\). Chọn khẳng định đúng.
Hàm số đồng biến trên khoảng \(\left( { - \ln \sqrt 2 ; + \infty } \right)\).
Hàm số đồng biến trên khoảng \(\left( { - \infty ; - \ln 2} \right)\).
Hàm số đồng biến trên khoảng \[\left( { - \infty ; - \ln \sqrt 2 } \right)\].
Hàm số đồng biến trên khoảng \(\left( { - \ln 2; + \infty } \right)\).
Hàm số \(y = {\log _{0,5}}\left( { - {x^2} + 4x} \right)\) đồng biến trên khoảng
\(\left( {2\,;\,4} \right)\).
\(\left( {0\,;\,4} \right)\).
\(\left( {2\,;\, + \infty } \right)\).
\(\left( {0\,;\,2} \right)\).
Hàm số \(y = x\ln x\) đồng biến trên khoảng nào sau đây?
\(\left( {\frac{1}{e}; + \infty } \right).\)
\(\left( {0;\frac{1}{e}} \right).\)
\(\left( {0; + \infty } \right).\)
\(\left( { - \frac{1}{e}; + \infty } \right).\)
Hàm số \(y = {x^2}{e^x}\) nghịch biến trên khoảng nào?
\(\left( { - 2;\,0} \right)\) .
\(\left( { - \infty ;\, - 2} \right)\) .
\(\left( { - \infty ;\,1} \right)\) .
\(\left( {1;\, + \infty } \right)\) .
Cho hàm số \[y = {\left( {0,5} \right)^{{x^2} - 8x}}\]. Hàm số đã cho nghịch biến trên khoảng
\[\left( {0;\,4} \right)\].
\[\left( {0;\,8} \right)\].
\[\left( {9;10} \right)\].
\[\left( { - \infty ;\,0} \right)\].
Hàm số \[y = {2^{{x^2} - 4x}}\]đồng biến trên khoảng
\(\left( { - \infty ;2} \right)\).
\(\left( {3;5} \right)\).
\(\left( {0; + \infty } \right)\).
\(\left( { - \infty ;3} \right)\).
Hàm số \(y = \ln \left( {{x^2} - 2x - 3} \right)\) đồng biến trên khoảng nào?
\(\left( { - \infty \,;\, - 1} \right)\).
\(\left( { - 1\,;\,3} \right)\).
\(\left( {1\,;\, + \infty } \right)\).
\(\left( {3\,;\, + \infty } \right)\).
Cho hàm số \(y = {\left( {\frac{3}{\pi }} \right)^{{x^2} + 2x + 3}}\). Tìm khẳng định đúng.
Hàm số luôn đồng biến trên \(\mathbb{R}\).
Hàm số luôn nghịch biến trên \(\mathbb{R}\).
Hàm số luôn nghịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\).
Hàm số luôn đồng biến trên khoảng \(\left( { - \infty ; - 1} \right)\).
Hàm số \(y = {x^2}{e^x}\) nghịch biến trên khoảng nào?
\(\left( { - 2;0} \right)\).
\(\left( { - \infty ; - 2} \right)\).
\(\left( { - \infty ;1} \right)\).
\(\left( {1; + \infty } \right)\).
