20 câu hỏi
I. Nhận biết
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Hàm số đã cho đồng biến trên khoảng nào?
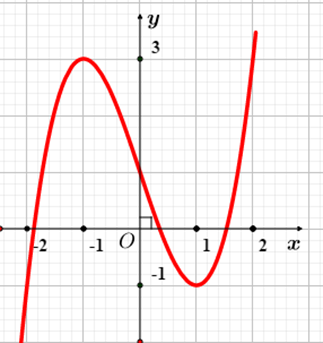
\(\left( { - 2\,;2} \right)\).
\(\left( {0\,;\,2} \right)\).
\(\left( { - 1\,;\,1} \right)\).
\(\left( {1\,;\,2} \right)\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
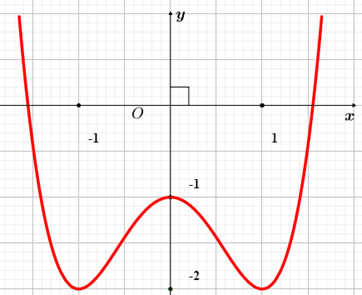
(0; 1).
(−∞; 1).
(−1; 1).
(−1; 0).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ sau
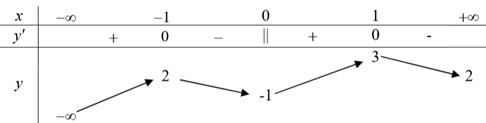
Mệnh đề nào dưới đây đúng?
Hàm số đồng biến trên khoảng \(\left( { - 1;\,3} \right)\).
Hàm số đồng biến trên khoảng \(\left( { - \infty ;\,2} \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - 2;\,1} \right)\).
Hàm số nghịch biến trên khoảng \(\left( {1;\,2} \right)\).
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và có đồ thị là đường cong như hình vẽ. Hàm số đạt cực đại tại điểm nào dưới đây?
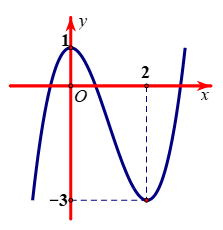
\(x = - 3\).
\(x = 1\).
\(x = 0\).
\(x = 2\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau
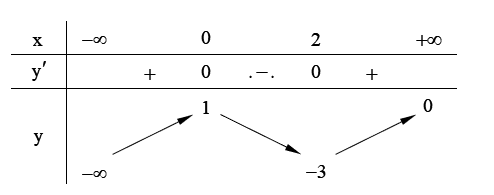
Giá trị cực đại của hàm số \(y = f\left( x \right)\) bằng
\[x = 0\].
\[x = 2\].
\[y = - 3\].
\[y = 1\].
II. Thông hiểu
Cho hàm số \[y = {x^3} + 3{x^2} - 9x + 15\]. Khẳng định nào sau đây là khẳng định sai?
Hàm số nghịch biến trên khoảng \[\left( { - 3;1} \right)\].
Hàm số đồng biến trên \[\left( { - 9; - 5} \right)\].
Hàm số đồng biến trên \[\mathbb{R}\] .
Hàm số đồng biến trên \[\left( {5; + \infty } \right)\].
Chọn mệnh đề đúng về hàm số \(y = \frac{{2x - 1}}{{x + 2}}\) .
Hàm số nghịch biến trên từng khoảng xác định của nó.
Hàm số đồng biến trên tập xác định của nó.
Hàm số đồng biến trên từng khoảng xác định của nó.
Hàm số nghịch biến trên tập xác định của nó.
Hàm số\[y = - {x^3} + 3{x^2} + 1\] nghịch biến khi \[x\] thuộc khoảng nào sau đây?
\[(0;2).\]
\[(0; + \infty ).\]
\[( - \infty ;2).\]
\[( - \infty ;0)\] và \[(2; + \infty ).\]
Cho hàm số \(y = {x^2}\left( {3 - x} \right)\). Mệnh đề nào sau đây là đúng?
Hàm số đã cho đồng biến trên khoảng \[\left( { - \infty ;0} \right)\].
Hàm số đã cho đồng biến trên khoảng \[\left( {2; + \infty } \right)\].
Hàm số đã cho đồng biến trên khoảng \[\left( {0;2} \right)\].
Hàm số đã cho đồng biến trên khoảng \[\left( { - \infty ;3} \right)\].
Hàm số nào sau đây nghịch biến trên toàn trục số?
\[y = {x^3} - 3{x^2}\].
\[y = - {x^3} + 3{x^2} - 3x + 2\].
\[y = - {x^3} + 3x + 1\].
\[y = {x^3}\].
Hàm số \(y = \frac{{1 - 2x}}{{ - x + 2}}\) có bao nhiêu cực trị?
\(3\).
\(0\).
\(2\).
\(1\).
Hàm số \(y = \frac{1}{3}{x^3} - 2{x^2} + 4x - 1\) có bao nhiêu điểm cực trị ?
1.
0.
2.
3.
Điểm cực tiểu của hàm số \(y = - {x^3} + 3x + 4\) là:
\(x = - 1.\)
\(x = 1.\)
\(x = - 3.\)
\(x = 3.\)
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
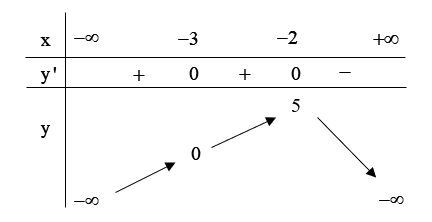
Trong các mệnh đề sau, có bao nhiêu mệnh đề sai?
I. Hàm số đã cho đồng biến trên các khoảng \(\left( { - \infty ; - 5} \right)\) và \(\left( { - 3; - 2} \right)\).
II. Hàm số đã cho đồng biến trên khoảng \(\left( { - \infty ;5} \right)\).
III. Hàm số đã cho nghịch biến trên khoảng \(\left( { - 2; + \infty } \right)\).
IV. Hàm số đã cho đồng biến trên khoảng \(\left( { - \infty ; - 2} \right)\).
\(1\).
\(2\).
\(3\).
\(4\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình dưới đây. Mệnh đề nào sau đây là đúng?
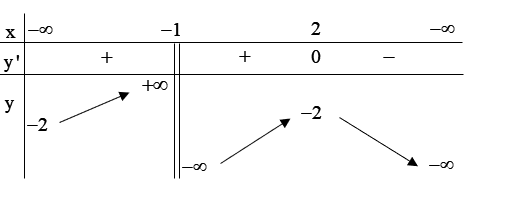
Hàm số đã cho đồng biến trên các khoảng \(\left( { - 2; + \infty } \right)\) và \(\left( { - \infty ; - 2} \right).\)
Hàm số đã cho đồng biến trên \(\left( { - \infty ; - 1} \right) \cup \left( { - 1;2} \right).\)
Hàm số đã cho đồng biến trên khoảng \(\left( {0;2} \right).\)
Hàm số đã cho đồng biến trên \(\left( { - 2;2} \right)\).
III. Vận dụng
Cho hàm số \(y = f(x)\). Hàm số \(y = f'(x)\) có đồ thị như hình vẽ:
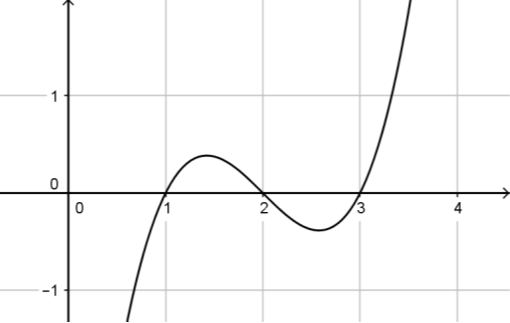
Khẳng định nào sau đây là khẳng định đúng?
Đồ thị hàm số \(y = f(x)\) cắt trục hoành tại ba điểm phân biệt.
Đồ thị hàm số \(y = f(x)\) có hai điểm cực trị.
Đồ thị hàm số \(y = f(x)\) có ba điểm cực trị.
Đồ thị hàm số \(y = f(x)\) có một điểm có một điểm cực trị.
Cho hàm số \[y = - \frac{1}{3}{x^3} + 4{x^2} - 5x - 17\]. Gọi hoành độ 2 điểm cực trị của đồ thị hàm số là \[{x_1},{x_2}\]. Khi đó, tích số \[{x_1}{x_2}\]có giá trị là:
\[5.\]
\[ - 5.\]
\[ - 4.\]
\[4.\]
Cho hàm số \[y = {x^3} - 3{x^2} - 2\]. Gọi \[a,b\]lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số đó. Giá trị của \[2{a^2} + b\] là:
\[ - 8\].
\[ - 2\].
\[2\].
4.
Một chuyển động thẳng xác định bởi phương trình \(s = \frac{1}{3}{t^3} - 3{t^2} + 5t + 2\) với \(t \ge 0\), trong đó t tính bằng giây và s tính bằng mét. Trong khoảng thời gian nào vận tốc của vật tăng?
(0; +∞).
(0; 3).
(−4; +∞).
(3; +∞).
Sau khi phát hiện một dịch bệnh, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ t là f(t) = 45t2 – t3, t = 0, 1, 2, …, 25. Nếu coi f(t) là hàm số xác định trên đoạn [0; 25] thì đạo hàm f'(t) được xem là tốc độ truyền bệnh (người/ngày) tại thời điểm t. Xác định khoảng thời gian mà tốc độ truyền bệnh giảm?
(0; 15).
(0; 10).
(15 ;25).
(10 ; 25).
