20 bài tập Một số bài toán thực tế liên quan đến nguyên hàm (có lời giải)

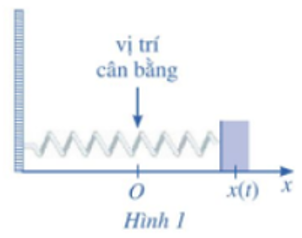
   Một con lắc lò xo dao động điều hoà theo phương ngang trên mặt phẳng không ma sát như Hình 1, có vận tốc tức thời cho bởi v(t) = 4cos t, trong đó t tính bằng giây và v(t) tính bằng centimét/giây. Tại thời điểm t = 0, con lắc đó ở vị trí cân bằng. Lập phương trình chuyển động của con lắc đó?

Khi được thả từ độ cao 20m, một vật rơi với gia tốc a = 10 m/s2. Sau khi rơi được t giây thì vật có tốc độ bao nhiêu và đi được quãng đường bao nhiêu?

Một hòn đá rơi từ móm đá có độ cao 150 m so với mặt đất theo phương thẳng đứng. Biết tốc độ rơi của hòn đá (tính theo đơn vị \({\rm{m}}/{\rm{s}}\) ) tại thời điểm t (tính theo giây) được cho bởi công thức \({\rm{v}}({\rm{t}})\) \( = 9,8{\rm{t}}\).

Quãng đường rơi được \(S\) của hòn đá tại thời điểm t được cho bởi công thức nào? Sau bao nhiêu giây thì hòn đá chạm đến mặt đất?

Một máy bay di chuyển ra đến đường băng và bắt đầu chạy đà để cất cánh. Giả sử vận tốc của máy bay khi chạy đà được cho bởi v(t)=5+3t (m/s), với t là thời gian (tính bằng giây) kể từ khi máy bay bắt đầu chạy đà. Sau 30 giây thì máy bay cất cánh rời đường băng. Quãng đường máy bay đã di chuyển từ khi bắt đầu chạy đà đến khi rời đường băng là bao nhiêu mét?

Một vườn ươm cây cảnh bán một cây sau 6 năm trồng và uốn tạo dáng. Tốc độ tăng trưởng trong suốt 6 năm được tính xấp xỉ bởi công thức \({h^\prime }(t) = 1,5t + 5\), trong đó \(h(t)({\rm{cm}})\) là chiều cao của cây khi kết thúc \(t\) (năm) (Nguồn: R. Larson and B. Edwards, Calculus 10e Cengage 2014). Cây con khi được trồng cao \(12\;{\rm{cm}}\).

a) Tìm công thức chỉ chiều cao của cây sau \(t\) năm.

b) Khi được bán, cây cao bao nhiêu centimét?

Tại một lễ hội dân gian, tốc độ thay đổi lượng khách tham dự được biểu diễn bằng hàm số

\({B^\prime }(t) = 20{t^3} - 300{t^2} + 1000t,\)trong đó \(t\) tính bằng giờ \((0 \le t \le 15),{B^\prime }(t)\) tính bằng khách/giờ.

(Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-I, Cornelsen 2016). Sau một giờ, 500 người đã có mặt tại lễ hội.

a) Viết công thức của hàm số \(B(t)\) biểu diễn số lượng khách tham dự lễ hội với \(0 \le t \le 15\).

b) Sau 3 giờ sẽ có bao nhiêu khách tham dự lễ hội?

c) Số lượng khách tham dự lễ hội lớn nhất là bao nhiêu?

d) Tại thời điểm nào thì tốc độ thay đổi lượng khách tham dự lễ hội là lớn nhất?

Đối vối các dự án xây dựng, chi phí nhân công lao động được tính theo số ngày công. Gọi \(m(t)\) là số lượng công nhân được sử dụng ở ngày thứt (kể từ khi khởi công dự án). Gọi \(M(t)\) là số ngày công được tính đến hết ngày thứ \(t\) (kể từ khi khởi công dự án). Trong kinh tế xây dựng, người ta đã biết rằng \({M^\prime }(t) = m(t)\).

Một công trình xây dựng dự kiến hoàn thành trong 400 ngày. Số lượng công nhân được sử dụng cho bởi hàm số: \(m(t) = 800 - 2t,\) trong đó \(t\) tính theo ngày \((0 \le t \le 400),m(t)\) tính theo người (Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016). Đơn giá cho một ngày công lao động là 400000 đồng. Tính chi phí nhân công lao động của công trình đó (cho đến lúc hoàn thành).

Một con lắc lò xo dao động điểu hoà theo phương ngang trên mặt phẳng không ma sát như Hình 1 , có vận tốc tức thời cho bởi \(v(t) = 4\cos t\), trong đó \(t\) tính bằng giây và \(v(t)\) tính bằng centimét/giây. Tại thời điểm \(t = 0\), con lắc đó ở vị trí cân bằng.

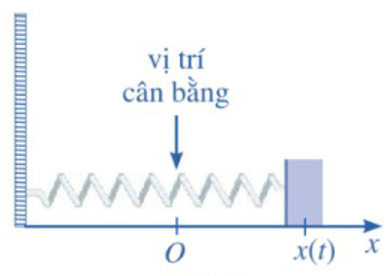
Phuơng trình chuyển động của con lắc đó đuợc xác định bằng cách nào?

 Cây cà chua khi trồng có chiều cao 5 cm. Tốc độ tăng chiều cao của cây cà chua sau khi trồng cho bởi hàm số: \[v(t) =  - 0,1{t^3} + {t^2}\]. trong đó t tính theo tuần, v(t) tính bằng centimet/tuần. Gọi h(t) (tính bằng centimet/tuần. Gọi h(t) (tính bằng centimet) là độ cao của cây cà chua ở tuần thứ t.

a) Viết công thức xác định hàm số h(t) \[\left( {t \ge 0} \right)\]

b) Giai đoạn tăng trưởng của cây cà chua đó kéo dài bao lâu?

c) Chiều cao tối đa của cây cà chua đó là bao nhiêu?

d) Vào thời điểm cây cà chua đó phát triền nhanh nhất thì cây cà chua sẽ cao bao nhiêu?

Một quần thể vi khuẩn ban đầu gồm 500 vi khuẩn , sau đó bắt đầu tăng trưởng. Gọi P(t) là số lượng vi khuẩn của quần thể đó tại thời điểm t, trong đó t tính theo ngày \[\left( {0 \le t \le 10} \right)\]. Tốc độ tăng trưởng của quần thể vi khuẩn đó cho bởi hàm số \[P'(t) = k\sqrt t \], trong đó k là hằng số. Sau 1 ngày, số lượng vi khuẩn của quần thể đó đã tăng thành 600 vi khuẩn. Tính số lượng vi khuẩn của quần thể đó sau 7 ngày (làm tròn kết quả đến hàng đơn vị)

Một viên đạn được bắn thẳng đứng lên trên từ mặt đất. Giả sử tại thời điểm \(t\) giây (coi \(t = 0\) là thời điểm viên đạn được bắn lên), vận tốc của nó được cho bởi \(v(t) = 160 - 9,8t(\;{\rm{m}}/{\rm{s}})\). Tìm độ cao của viên đạn (tính từ mặt đất):

a) Sau \(t = 5\) giây;

b) Khi nó đạt độ cao lớn nhất (làm tròn kết quả đến chữ số thập phân thứ nhất).

Một ô tô đang chạy với tốc độ \(19\;{\rm{m}}/{\rm{s}}\) thì hãm phanh và chuyển động chậm dần với tốc độ \(v(t) = 19 - 2t(\;{\rm{m}}/{\rm{s}})\). Kề từ khi hãm phanh, quãng đường ô tô đi được sau 1 giây, 2 giây, 3 giây là bao nhiêu?

Kí hiệu \(h(x)\) là chiều cao của một cây (tính theo mét) sau khi trồng \(x\) năm. Biết rằng sau năm đầu tiên cây cao \(2\;{\rm{m}}\). Trong 10 năm tiếp theo, cây phát triền với tốc độ \({h^\prime }(x) = \frac{1}{x}(\;{\rm{m}}/{\rm{nam}})\).

a) Xác định chiều cao của cây sau \(x\) năm \((1 \le x \le 11)\).

b) Sau bao nhiêu năm cây cao \(3\;{\rm{m}}\) ?

Một quả bóng được ném lên từ độ cao \(24,5\;{\rm{m}}\) với vận tốc được tính bởi công thức \(v(t) =  - 9,8t + 19,6(\;{\rm{m}}/{\rm{s}})\).

a) Viết công thức tính độ cao của quả bóng theo thời gian \(t\).

b) Sau bao nhiêu lâu kể từ khi ném lên thì quả bóng chạm đất?

Một chiếc xe đang chuyển động với tốc độ \({v_0} = 10\;{\rm{m}}/{\rm{s}}\) thì tăng tốc với gia tốc không đổi \(a = 2\;{\rm{m}}/{{\rm{s}}^2}\). Tính quãng đường xe đó đi được trong 3 giây kề từ khi bắt đầu tăng tốc.

Doanh thu bán hàng của một công ty khi bán một loại sản phẩm là số tiền R(x) (triệu đồng) thu được khi x đơn vị sản phẩm được bán ra. Tốc độ biến động (thay đổi) của doanh thu khi x đơn vị sản phẩm đã được bản là hàm số \[{M_R}(x) = R'(x)\]. Một công ty công nghệ cho biết, tốc độ biến đổi của doanh thu khi bán một loại con chíp của hãng được cho bởi \[{M_R}\left( x \right) = 300 - 0,1x\], ở đó x là số lượng chíp đã bán. Tìm doanh thu của công ty khi đã bản 1.000 con chíp.

  Một xe ô tô đang chạy với tốc độ \(72\;{\rm{km}}/{\rm{h}}\) thì người lái xe bất ngờ phát hiện chướng ngại vật trên đường cách đó \(80\;{\rm{m}}\). Người lái xe phản ứng một giây sau đó bằng cách đạp phanh khẩn cấp. Kể từ thời điểm này, ô tô chuyển động chậm dần đều với tốc độ \(v(t) =  - 10t + 30(\;{\rm{m}}/{\rm{s}})\), trong đó \(t\) là thời gian tính bằng giây kể từ lúc đạp phanh. Gọi \(s(t)\) là quãng đường xe ô tô đi được trong \(t\) (giây) kể từ lúc đạp phanh.

a) Lập công thức biểu diễn hàm số \(s(t)\).

b) Thời gian kể từ lúc đạp phanh đến khi xe ô tô dừng hẳn là bao nhiêu giây?

c) Quãng đường xe ô tô đã di chuyển kể từ lúc người lái xe phát hiện chướng ngại vật trên đường đến khi xe ô tô dừng hẳn là bao nhiêu mét? Xe ô tô liệu có gặp tai nạn do va chạm với chướng ngại vật trên đường hay không?

Mực nược trong hồ chứa của nhà máy điện thuỷ triều thay đổi trong suốt một ngày do nước chảy ra (khi thuỷ triều xuống) và nước chảy vào (khi thuỷ triều lên) (Hình 2). Tốc độ thay đổi của mực nước trong hồ chứa được cho bởi hàm số \({h^\prime }(t) = \frac{1}{{216}}\left( {5{t^2} - 120t + 480} \right){\rm{, }}\)trong đó \(t\) tính bằng giờ \((0 \le t \le 24),{h^\prime }(t)\) tính bằng mét/giờ. Tại thời điểm \(t = 0\), mực nước trong hồ chứa là \(6\;{\rm{m}}\) (Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016).

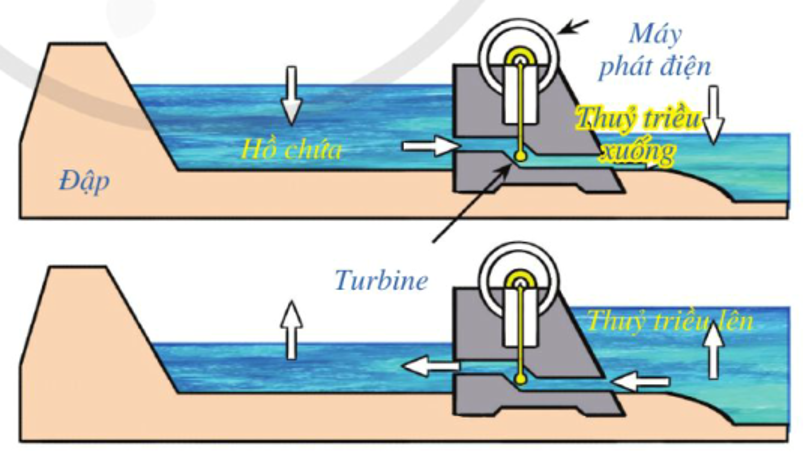
a) Viết công thức xác định hàm số \(h(t)\).

b) Mực nước trong hồ chứa cao nhất và thấp nhất bằng bao nhiêu (làm tròn kết quả đến hàng phần mười của mét)?

c) Mực nước trong hồ chứa thay đổi nhanh nhất khi nào? Tốc độ thay đổi của mực nước trong hồ chứa khi đó là bao nhiêu?

Một xe ô tô đang chạy với vận tốc 72 km/h thì người lái xe phát hiện chướng ngại vật trên đường cách đó 80 m. Người lái xe phản ứng một giây sau đó bằng cách đáp phanh khẩn cấp. Kể từ thời điểm này, ô tô chuyển động chậm dần đều với tố độ v(t) = -10t + 30 (m/s), trong đó t là thời gian tính bằng giây kể từ lúc đạp phan. Gọi S(t) là quãng đường xe ô tô đi được trong t giây kể từ lúc đạp phhan.

a) Lập công thức biểu diễm hàm số s(t)

b) Thời gian kể từ lúc đạp phanh đến khi xe dừng lại hẳn là bao nhiêu giây?

c) Quãng đường xe ô tô đã di chuển kể từ lúc người lái xe phát hiện chướng ngại vật trên đường đến khi xe dừng lại hẳn là bao nhiêu mét? Xeo ô tô có gặp tai nạn do va chạm với chướng ngại vật trên đường hay không?