Quiz

100 câu trắc nghiệm Phương trình lượng giác nâng cao (P3)

Admin20 câu hỏiToánLớp 11

Bắt đầu ngay

20 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

Số nghiệm thuộc [ $\frac{π}{14}$ ; $\frac{69 π}{10}$ ) của phương trình 2sin3x.(1 – 4sin²x) = 1 là:

A. 40

B. 32

C. 38

D. 46

2. Nhiều lựa chọn

Các nghiệm thuộc khoảng (0; $\frac{π}{2}$ ) của phương trình sin³x.cos3x + cos³x.sin3x = $\frac{3}{8}$

3. Nhiều lựa chọn

Phương trình $2 \sin (3 x + \frac{π}{4}) = \sqrt{1 + 8 \sin 2 x . \cos^{2} 2 x}$ có nghiệm là:

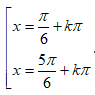
A. Phương trình 2sin(3x + pi/4) = căn(1 + 8sin2x.cos^2 2x) có nghiệm là: A.x=pi/6+kpi hoặc x=5pi/6+kpi (ảnh 2)

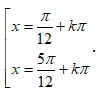
B. Phương trình 2sin(3x + pi/4) = căn(1 + 8sin2x.cos^2 2x) có nghiệm là: A.x=pi/6+kpi hoặc x=5pi/6+kpi (ảnh 3)

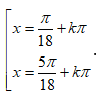
C. Phương trình 2sin(3x + pi/4) = căn(1 + 8sin2x.cos^2 2x) có nghiệm là: A.x=pi/6+kpi hoặc x=5pi/6+kpi (ảnh 4)

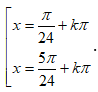
D. Phương trình 2sin(3x + pi/4) = căn(1 + 8sin2x.cos^2 2x) có nghiệm là: A.x=pi/6+kpi hoặc x=5pi/6+kpi (ảnh 5)

4. Nhiều lựa chọn

Tìm số nghiệm x ∈ (0; π) của phương trình 5cosx + sinx - 3 = $\sqrt{2}$ sin(2x + $\frac{π}{4}$ ) (*)

A: 1

B: 2

C: 3

D: 4

5. Nhiều lựa chọn

Tìm m để phương trình 2sin²x – (2m + 1)sinx + m = 0 có nghiệm x ∈ ( $\frac{- π}{2}$ ; 0).

A. -1 < m

B. 1 < m

C. -1 < m < 0

D. 0 < m < 1

6. Nhiều lựa chọn

Phương trình $\sin^{3} x + \cos^{3} x + \sin^{3} x . cotx + \cos^{3} x . tanx = \sqrt{2 \sin 2 x}$ có nghiệm là:

A. x = $\frac{π}{8}$ + kπ

B. x = $\frac{π}{4}$ + kπ

C. x = $\frac{π}{4}$ + k2π

D. x = $\frac{3 π}{4}$ + k2π

7. Nhiều lựa chọn

Phương trình $\frac{\sin^{4} x + \cos^{4} x}{\sin 2 x} = \frac{1}{2} (tanx + cotx)$ có nghiệm là:

A. x = $\frac{π}{2}$ + kπ.

B. x = $\frac{π}{3}$ + k2π

C. x = $\frac{π}{4}$ + k $\frac{π}{2}$

D.Vô nghiệm

8. Nhiều lựa chọn

Cho phương trình cos2x.cosx + sinx.cos3x = sin2x.sinx - sin3x.cosx và các họ số thực:

I. x = $\frac{π}{4}$ + kπ, k ∈ Z.

II. x = $\frac{- π}{2}$ + k2π, k ∈ Z.

III. x = $\frac{- π}{14}$ + $\frac{k 2 π}{7}$ , k ∈ Z.

IV. x = $\frac{π}{7}$ + $\frac{k 4 π}{7}$ , k ∈ Z.

Chọn trả lời đúng: Nghiệm của phương trình là:

A. I, II

B. I, III

C. II, III

D. II, IV.

9. Nhiều lựa chọn

Tổng các nghiệm thuộc khoảng (0;2018) của phương trình $\sin^{4} \frac{x}{2} + \cos^{4} \frac{x}{2} = 1 - 2 \sin x$ là

A. 207046π

B. 206403π

C. 205761π

D. 204603π

10. Nhiều lựa chọn

Tổng 2 nghiệm âm liên tiếp lớn nhất của phương trình 4sin³x – sinx – cosx = 0 bằng:

D. -π

11. Nhiều lựa chọn

Cho phương trình sinx.cosx - sinx - cosx + m = 0, trong đó m là tham số thực. Để phương trình có nghiệm, các giá trị thích hợp của m là

A. $- 2 \leq m \leq - \frac{1}{2} - \sqrt{2}$

B. $- \frac{1}{2} - \sqrt{2} \leq m \leq 1$

C. $1 \leq m \leq \frac{1}{2} + \sqrt{2}$

D. $\frac{1}{2} + \sqrt{2} \leq m \leq 2$

12. Nhiều lựa chọn

Phương trình 2sin2x - 3 $\sqrt{6}$ |sinx + cosx| + 8 = 0 có nghiệm là

A. Phương trình 2sin2x - 3căn(6)|sinx + cosx| + 8 = 0 có nghiệm là: A.x=pi/3+kpi hoặc x= 5pi/3+kpi ,k thuộc Z (ảnh 2)

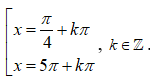
B. Phương trình 2sin2x - 3căn(6)|sinx + cosx| + 8 = 0 có nghiệm là: A.x=pi/3+kpi hoặc x= 5pi/3+kpi ,k thuộc Z (ảnh 3)

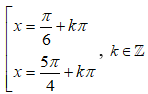
C. Phương trình 2sin2x - 3căn(6)|sinx + cosx| + 8 = 0 có nghiệm là: A.x=pi/3+kpi hoặc x= 5pi/3+kpi ,k thuộc Z (ảnh 4)

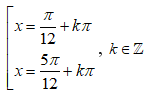
D. Phương trình 2sin2x - 3căn(6)|sinx + cosx| + 8 = 0 có nghiệm là: A.x=pi/3+kpi hoặc x= 5pi/3+kpi ,k thuộc Z (ảnh 5)

13. Nhiều lựa chọn

Tổng các nghiệm của phương trình sinx.cosx + |cosx + sinx| = 1 trên (0; 2π) là:

A. π

B. 2π

C. 3π

D. 4π

14. Nhiều lựa chọn

Có bao nhiêu giá trị nguyên của m để phương trình: sin2x + $\sqrt{2}$ sin(x - $\frac{π}{4}$ ) - m = 0 có nghiệm.

A.3

B.4

C.5

D.6

15. Nhiều lựa chọn

Giải phương trình $5 (sinx + \frac{\sin 3 x + \cos 3 x}{1 + 2 \sin 2 x}) = \cos 2 x + 3$

A. $x = \pm \frac{π}{3} + k 2 π, k \in ℤ$

B. x = ± $\frac{π}{6}$ + k2π, k ∈ $ℤ$

C. $x = \pm \frac{π}{3} + k π, k \in ℤ$

D. x = ± $\frac{π}{6}$ + kπ, k ∈ $ℤ$

16. Nhiều lựa chọn

Cho phương trình $\frac{1}{2} \cos 4 x + \frac{4 tanx}{1 + \tan^{2} x} = m$ . Để phương trình vô nghiệm, các giá trị của tham số m phải thỏa mãn điều kiện:

A. $- \frac{5}{2}$ ≤ m ≤ 0

B. m > 1

C. 0 < m

D. m $\leq$ $- \frac{5}{2}$ hay m > $\frac{3}{2}$ .

17. Nhiều lựa chọn

Nghiệm phương trình: $\frac{cosx (cosx + 2 sinx) + 3 sinx (sinx + \sqrt{2})}{\sin 2 x - 1} = 1$

A. x = ± $\frac{π}{4}$ + k2π, k ∈ Z

B. x = $- \frac{π}{4}$ + kπ, k ∈ Z

C. x = $- \frac{π}{4}$ + k2π, x = $- \frac{3 π}{4}$ + k2π, k ∈ Z

D. x = $- \frac{π}{4}$ + k2π, k ∈ Z

18. Nhiều lựa chọn

Cho phương trình cos5x.cosx = cos4x.cos2x + 3cos²x + 1. Các nghiệm thuộc khoảng (-π; π) của phương trình là:

19. Nhiều lựa chọn

Giải phương trình 3tan²x + 4sin²x - 2 $\sqrt{3}$ tanx - 4sinx + 2 = 0

A. x = ± $\frac{π}{6}$ + k2π, k ∈ Z

B. x = $\frac{π}{6}$ + kπ, k ∈ Z

C. x = $- \frac{π}{4}$ + k2π, $- \frac{π}{6}$ + k2π, k ∈ Z

D. Tất cả sai

20. Nhiều lựa chọn

Giải phương trình sin3x(cosx - 2sin3x) + cos3x(1 + sinx - 2cos3x) = 0

A. x = ± $\frac{π}{3}$ + k2π, k ∈ Z

B. x = $\frac{π}{4}$ + kπ, k ∈ Z

C. x = $- \frac{π}{4}$ + k2π, x = $- \frac{π}{6}$ + k2π,k ∈ Z

D. Vô nghiệm

Gợi ý cho bạn

QuizToán - Tốt nghiệp THPT

Trắc nghiệm củng cố

2 câu hỏi3 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi5 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi28 lượt thi

QuizToán - Lớp 12

10 bài tập Xác định các yếu tố cơ bản của đường thẳng trong không gian có lời giải

10 câu hỏi16 lượt thi

QuizToán - Lớp 12

10 bài tập Vận dụng kiến thức phương trình mặt phẳng vào giải quyết bài toán liên quan đến thực tế có lời giải

10 câu hỏi14 lượt thi

QuizToán - Lớp 12

10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Khoảng cách từ một điểm đến một mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình mặt phẳng đi qua 1 điểm kèm điều kiện song song với mặt phẳng khác có lời giải

10 câu hỏi13 lượt thi

Facebook Youtube