(Trả lời ngắn) 9 bài tập Công thức tính góc trong không gian (có lời giải)
9 câu hỏi
Trong không gian với hệ trục tọa độ\[Oxyz\], cho điểm \[H\left( {2;1;2} \right)\], \[H\] là hình chiếu vuông góc của gốc tọa độ \[O\] xuống mặt phẳng\[\left( P \right)\]. Tính số đo góc giữa mặt \[\left( P \right)\] và mặt phẳng \[\left( Q \right):x + y - 11 = 0\] theo đơn vị độ.
Trong không gian \[Oxyz\], cho mặt phẳng \[(P)\]có phương trình \[x - 2y + 2z - 5 = 0\]. Xét mặt phẳng \[(Q):x + (2m - 1)z + 7 = 0\], với \[m\]là tham số thực. Có bao nhiêu giá trị của \[m\] để \[(P)\] tạo với \[(Q)\] góc \[\frac{\pi }{4}\].
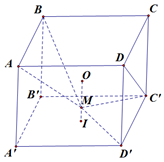
Cho hình lập phương \[ABCD.A'B'C'D'\] có tâm \(O\). Gọi \(I\) là tâm của hình vuông \(A'B'C'D'\) và điểm \(M\) thuộc đoạn \(OI\) sao cho \(MO = 2MI\) (tham khảo hình vẽ). Tính sin của góc tạo bởi hai mặt phẳng \(\left( {MC'D'} \right)\) và \(\left( {MAB} \right)\) (làm tròn kết quả đến hàng phần trăm).
Cho hình lăng trụ \(ABC.A'B'C'\)có đáy \(ABC\) là tam giác vuông tại \(A\), \(AB = a\),\(AC = a\sqrt 3 \). Hình chiếu vuông góc của \(A'\) lên mặt phẳng \(\left( {ABC} \right)\) là trung điểm \(H\) của \(BC\), \(A'H = a\sqrt 5 \). Gọi \(\varphi \) là góc giữa hai đường thẳng \(A'B\) và \(B'C\). Tính \(\cos \varphi \) (làm tròn kết quả đến hàng phần trăm).
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\), có \(AB = a,\,AD = a\sqrt 2 ,\)góc giữa \(A'C\)và mặt phẳng \(\left( {ABCD} \right)\) bằng . Gọi \(H\)là hình chiếu vuông góc của \(A\)trên \(A'B\)và \(K\) là hình chiếu vuông góc của \(A\) trên \(A'D.\) Tính góc giữa hai mặt phẳng\(\left( {AHK} \right)\) và \(\left( {ABB'A'} \right)\) (đơn vị: độ).
Cho hình lăng trụ đứng \[ABC.A'B'C'\]có . Gọi \[M,{\rm{ }}N\]lần lượt là trung điểm của \[B'C'\]và \[CC'\]. Biết thể tích khối lăng trụ \[ABC.A'B'C'\]bằng \[\frac{{\sqrt 3 {a^3}}}{4}\]. Gọi \[\alpha \]là góc giữa mặt phẳng \[\left( {AMN} \right)\]và mặt phẳng \[\left( {ABC} \right)\], tính \[\cos \alpha \] ta được kết quả là \[\frac{{\sqrt 3 }}{a}\]. Xác định a.
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(B\), \(AC = 2a\), tam giác \(SAB\) và tam giác \(SCB\) lần lượt vuông tại \(A\), \(C\). Khoảng cách từ \(S\) đến mặt phẳng \[\left( {ABC} \right)\] bằng \(2a\). Tính côsin của góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCB} \right)\) ta được kết quả là \(\frac{a}{b}\), với \(\frac{a}{b}\) là phân số tối giản. Tính a + b.
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác cân đỉnh \(A\). Biết \(BC = a\sqrt 3 \) và , cạnh bên \(AA' = a\). Gọi \(M\) là điểm thỏa mãn \(2\overrightarrow {CM} = 3\overrightarrow {CC'} \). Gọi \(\alpha \) là góc tạo bởi hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {AB'M} \right)\), khi đó tính \(\sin \alpha \) (làm tròn kết quả đến hàng phần trăm).
Cho khối tứ diện \(ABCD\) có \(BC = 3\), \(CD = 4\), \(\widehat {ABC} = \widehat {ADC} = \widehat {BCD} = {90^0}\). Góc giữa đường thẳng \(AD\) và \(BC\) bằng . Tính côsin góc giữa hai phẳng \(\left( {ABC} \right)\) và \(\left( {ACD} \right)\) (làm tròn kết quả đến hàng phần mười) .








