10 bài tập Một số dạng toán thực tế liên quan đến Công thức tính góc trong không gian (có lời giải)

Trên một sân khấu đã thiết lập sẵn một hệ toạ độ Oxyz. Tính góc giữa tia sáng có phương trình \(d:\left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = 1 + t}\\{z = 1 + t}\end{array}} \right.\) và mặt sàn sân khấu có phương trình \(z = 0\).

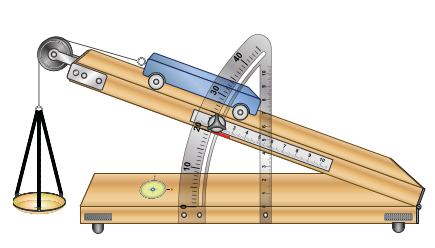
Để làm thí nghiệm về chuyền động trong mặt phẳng nghiêng, người làm thí nghiệm đã thiết lập sẵn một hệ toạ độ Oxyz. Tính góc giũ̃a mặt phằng nghiêng \((P)\) : \(4x + 11z + 5 = 0\) và mặt \({\rm{sàn}}(Q):z - 1 = 0\).

Trên một cánh đồng điện mặt trời, người ta đã thiết lập sẵn một hệ tọa độ Oxyz. Hai tấm pin năng lượng lần lượt nằm trong hai mặt phẳng \((P):2x + 2z + 1 = 0\) và \(\left( {{P^\prime }} \right):x + z + 7 = 0\).

a) Tính góc giữa \((P)\) và \(\left( {{P^\prime }} \right)\).

b) Tính góc hợp bời \((P)\) và \(\left( {{P^\prime }} \right)\) với mặt đất \((Q)\) có phương trình \(z = 0\).

Trên một sườn núi (có độ nghiêng đều), người ta trồng một cây thông và muốn giữ nó không bị nghiêng bằng hai sợi dây neo như Hình 34. Giả thiết cây thông mọc thẳng đứng và trong một hệ toạ độ phù hợp, các điểm \(O\) (gốc cây thông) và A, B (nơi buộc dây neo) có tọa độ tương ứng là \(O(0;0;0),A(3; - 4;2)\), \(B( - 5; - 2;1)\), đơn vị trên mỗi trục toạ độ là mét.

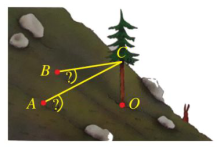
Biết rằng hai dây neo đều được buộc vào cây thông tại điểm \((0;0;5)\) và được kéo căng tạo thành các đoạn thẳng.

a) Tính độ dài của mỗi dây neo được sử dụng.

b) Tính góc tạo bởi mỗi dây neo và mặt phẳng sườn núi (làm tròn kết quả đến hàng đơn vị của độ).

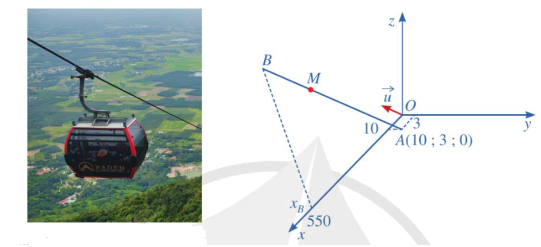
Trong không gian với hệ toạ độ Oxyz, một cabin cáp treo xuất phát từ điểm \(A(10;3;0)\) và chuyển động đều theo đường cáp có vectơ chỉ phương là \(\vec u = (2; - 2;1)\) vởi tốc độ là \(4,5\;{\rm{m}}/{\rm{s}}\) (đơn vị trên mỗi trục toạ độ là mét) (Hình 35).

a) Viết phương trình đường cáp.

b) Giả sử sau \(t(\;{\rm{s}})\) kể từ lúc xuất phát \((t \ge 0)\), cabin đến điểm \(M\). Tìm tọa độ của điểm \(M\).

c) Cabin dừng ở điểm \(B\) có hoành độ \({x_B} = 550\). Tìm độ dài quãng đường AB (làm tròn kết quả đến hàng đơn vị của mét).

d) Đường cáp AB tạo với mặt phẳng (Oxy) góc bao nhiêu độ (làm tròn kết quả đến hàng đơn vị của độ)?

Một mái nhà hình tròn được đặt trên ba cây cột trụ (H.5.33). Các cây cột vuông góc với mặt sàn nhà phẳng và có độ cao lần lượt là \(7\;{\rm{m}},6\;{\rm{m}},5\;{\rm{m}}\). Ba chân cột là ba đỉnh của một tam giác đều trên mặt sàn nhà với cạnh dài 4 m . Hỏi mái nhà nghiêng với mặt sàn nhà một góc bao nhiêu độ?

Kim tự tháp Kheops ở Ai Câpp có dạng hình chóp S.ABCD, có đáy là hình vuông với cạnh dài 230 m , các cạnh bên bằng nhau và dài 219 m (theo britannica.com) (H.5.38). Tính góc giữa hai mặt phẳng \((SAB)\) và (SBC).

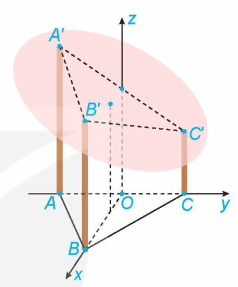
Trong một bể hình lập phương cạnh 1 m có chứa một ít nước. Người ta đặt đáy bể nghiêng so với mặt phẳng nằm ngang. Biết rằng, lúc đó mặt nước có dạng hình bình hành ABCD và khoảng cách từ các điểm A, B, C đến đáy bể tương ứng là \(40\;{\rm{cm}},44\;{\rm{cm}},48\;{\rm{cm}}\).

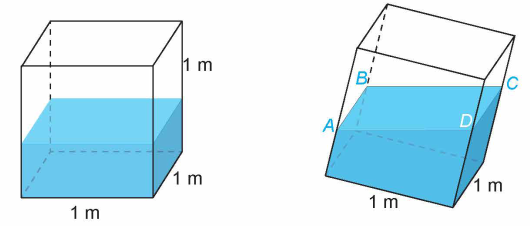
a) Khoảng cách từ điểm \(D\) đến đáy bể bằng bao nhiêu centimét? (Tính gần đúng, lấy giá trị nguyên.)

b) Đáy bể nghiêng so với mặt phẳng nằm ngang một góc bao nhiêu độ?

Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục toạ độ là kilômét), một máy bay đang ở vị trí \(A(3,5; - 2;0,4)\) và sẽ hạ cánh ở vị trí \(B(3,5;5,5;0)\) trên đường băng EG (Hình 37 ).

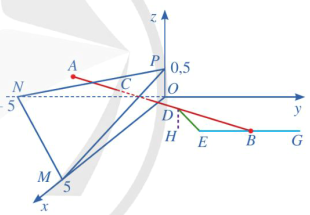
a) Viết phương trình đường thẳng AB.

b) Hãy cho biết góc trượt (góc giữa đường bay AB và mặt phẳng nằm ngang (Oxy) có nằm trong phạm vi cho phép từ 2,5⁰ đến 3,5⁰ hay không.

c) Có một lớp mây được mô phỏng bởi một mặt phẳng \((\alpha )\) đi qua ba điểm \(M(5;0;0)\), \(N(0; - 5;0),P(0;0;0,5)\). Tìm tọa độ của điểm \(C\) là vị trí mà máy bay xuyên qua đám mây để hạ cánh.

d) Tìm toạ độ của điểm \(D\) trên đoạn thẳng AB là vị trí mà máy bay ở độ cao 120 m .

e) Theo quy định an toàn bay, người phi công phải nhìn thấy điểm đầu \(E(3,5;6,5;0)\) của đường băng ở độ cao tối thiểu là 120 m . Hỏi sau khi ra khỏi đám mây, người phi công có đạt được quy định an toàn đó hay không? Biết rằng tầm nhìn của người phi công sau khi ra khỏi đám mây là 900 m (Nguồn: R.Larson and B.Edwards, Calculus 10e, Cengage, 2014).