(Trả lời ngắn) 32 bài tập GTLN, GTNN của hàm số (có lời giải)

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=\sin x + \cos x$   trên đoạn $\left[0;2\pi \right]$ .

Trả lời: $ma{x}_{\left[0;2\pi \right]}y=y\left(\frac{\pi }{4}\right)=\sqrt{2};mi{n}_{\left[0;2\pi \right]}y=y\left(\frac{5\pi }{4}\right)=-\sqrt{2}$.

Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số $y=f\left(x\right)=x^3-3x^2-9x+5$   trên đoạn $\left[0;5\right]$ .

Trả lời: $ma{x}_{\left[0;5\right]}f\left(x\right)=10,mi{n}_{\left[0;5\right]}f\left(x\right)=-22$ .

Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) $f\left(x\right)=2x^3-9x^2+12x+1$  trên đoạn [0;3]
b) $g\left(x\right)=x+\frac{1}{x}$  trên khoảng $\left(0;5\right)$
c) $h\left(x\right)=x\sqrt{2-x^2}$

Trả lời:  

a) $mi{n}_{\left[0;3\right]}f\left(x\right)=f\left(0\right)=1$ và $ma{x}_{\left[0;3\right]}f\left(x\right)=f\left(3\right)=10$

b) $mi{n}_{\left(0;5\right)}f\left(x\right)=f\left(1\right)=2$ và hàm số không tồn tại giá trị lớn nhất trên khoảng $\left(0;5\right)$
c) $mi{n}_{D}f\left(x\right)=f\left(-1\right)$ và $ma{x}_{D}f\left(x\right)=f\left(1\right)=1$

Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) $y=x^3-12x+1$  trên đoạn [-1;3]
b) $y=-x^3+24x^2-180x+400$  trên đoạn [3;11]
c) $y=\frac{2x+1}{x-2}$  trên đoạn $[3;7]$
d) $y=\sin 2x$  trên đoạn $\left[0;\frac{7\pi }{12}\right]$

Trả lời:  

a) $ma{x}_{\left[-1;3\right]}y=y\left(-1\right)=12$  và $mi{n}_{\left[-1;3\right]}y=y\left(2\right)=-15$
b)  $ma{x}_{\left[3;11\right]}y=y\left(3\right)=49$  và $mi{n}_{\left[3;11\right]}y=y\left(6\right)=-32$
c) $ma{x}_{\left[3;7\right]}y=y\left(3\right)=7$  và $mi{n}_{\left[3;7\right]}y=y\left(7\right)=3$
d) $ma{x}_{\left[0;\frac{7\pi }{12}\right]}y=y\left(\frac{\pi }{4}\right)=1$  và $mi{n}_{\left[0;\frac{7\pi }{12}\right]}y=y\left(\frac{7\pi }{12}\right)=-\frac{1}{2}$

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số có đồ thị được cho ở Hình 5

Trả lời:

a)  $ma{x}_{\left[1;6\right]}f\left(x\right)=f\left(1\right)=6$  và $mi{n}_{\left[1;6\right]}f\left(x\right)=f\left(5\right)=1$
b) $ma{x}_{\left[-3;3\right]}g\left(x\right)=g\left(-3\right)=g\left(-1\right)=1$  và $mi{n}_{\left[-1;3\right]}g\left(x\right)=g\left(1\right)=7$

Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số $g\left(x\right)=x+\frac{4}{x^2}$   trên đoạn [1;4]

Trả lời: $mi{n}_{\left[1;4\right]}g\left(x\right)=g\left(2\right)=3$  và $ma{x}_{\left[1;4\right]}g\left(x\right)=g\left(1\right)=5$

Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số $y=x-2+\frac{1}{x}$  trên khoảng $\left(0;+\infty \right)$ .

Trả lời: $mi{n}_{\left(0;+\infty \right)}y=y\left(1\right)=0$ ; hàm số không có giá trị lớn nhất trên khoảng $\left(0;+\infty \right)$ .

Tìm giá trị lôn nhất và giá trị nhỏ nhất (nếu có) của hàm số $f\left(x\right)=\frac{x^2+9}{x}$  trên khoảng $\left(0;+\infty \right)$ .

Trả lời: $mi{n}_{\left(0;+\infty \right)}f\left(x\right)=6$  tại $x=3$  và hàm số $f\left(x\right)$   không có giá trị lớn nhất.

Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số $y=2\sqrt{1-x^2}+x^2$

Trả lời: $ma{x}_{D}y=y\left(0\right)=2$  và $mi{n}_{D}y=y\left(-1\right)=y\left(1\right)=1$

Tìm giá trị lớn nhất và giá trị nhó nhất của hàm số:  $f\left(x\right)={\sin }^{4}x+{\cos }^{4}x$

Trả lời: $mi{n}_{x\in \mathrm{ℝ}}f\left(x\right)=\frac{1}{2}$

Hộp sữa $1l$  được thiết kế dạng hình hộp chữ nhật với đáy là hình vuông cạnh $x cm$ . Tìm $x$  để diện tích toàn phần của hộp nhỏ nhất.

Trả lời:  $x=1 cm$  thì diện tích toàn phần của hộp nhỏ nhất và bằng $6 c{m}^2$

Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y=f\left(x\right)=x+\frac{1}{x}=7$  trên khoảng $\left(0;+\infty \right)$ .

Trả lời: Trên khoảng $\left(0;+\infty \right)$ , hàm số có giá trị nhỏ nhất là -5 tại $x=1$ . Hàm số $f\left(x\right)$  không có giá trị lớn nhất trên khoảng $\left(0;+\infty \right)$ .

Tìm giá trị nhỏ nhất của các hàm số sau:
a) $y=x^3-3x-4$  trên nửa khoảng [-3;2)                     

b) $y=\frac{3x^2-4x}{x^2-1}$  trên khoảng $\left(-1;+\infty \right)$

Trả lời: 

a) $mi{n}_{\left[-3;2\right]}y=y\left(-3\right)=-22$

b) hàm số không tồn tại giá trị nhỏ nhất trên khoảng $\left(-1;+\infty \right)$   

Tìm tất cả các giá trị của tham số \[m\] để hàm số \[f(x) = {x^3} + 3{x^2} + {m^2} - 5\] có giá trị lớn nhất trên đoạn \[\left[ { - 1\,;\,2} \right]\] là 19.

Trả lời: \[m = 2\] và \[m =  - 2\].

Cho hàm số \(y = \frac{{x + m}}{{x + 1}}\) \(m > 1\). Với giá trị nào của tham số \(m\) để hàm số có giá trị lớn nhất trên \(\left[ {\,1\,;\,4\,} \right]\) bằng 3.

Trả lời: \(m = 5\).

Trong một thí nghiệm y học, người ta cấy 1000 vi khuẩn vào môi trường dinh đưỡng. Bằng thực nghiệm, người ta xác định được số lượng vi khuẩn thay đổi theo thời gian bởi công thức: $N\left(t\right)=1000+\frac{100t}{100+t^2}$9(con)trong đó  là thời gian tính bằng giây Tính số lượng vi khuẩn lôn nhất kể từ khi thực hiện cấy vi khuẩn vào môi trường dinh dưỡng.

Trả lời:  Số lượng vi khuẩn lôn nhất kể từ khi thực hiện cấy vi khuẩn vào môi trường dinh dưởng là 1005 con.

Tam giác vuông có cạnh huyền bằng $5 cm$  có thể có diện tích lớn nhất bằng bao nhiêu?

Trả lời:  diện tích lớn nhất của tam giác là $\frac{5}{2}$

Khối lượng $q\left(kg\right)$  của một mặt hàng mà cửa tiệm bán được trong một ngày phụ thuộc vào giá bán $p$   (nghìn đồng/kg) theo công thức $p=15-\frac{1}{2}q$ . Doanh thu từ việc bán mặt hàng trên của cửa tiệm được tính theo công thức $R=pq$ . Tìm giá bán mỗi kilôgam sản phẩm để đạt được doanh thu cao nhất và xác định doanh thu cao nhất đó.

Trả lời:   $ma{x}_D=y\left(7,5\right)=112,5$

Một hợp tác xã nuôi cá trong hồ. nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng: P(n) = 480 - 20n (gam). Hỏi phải thả bao nhiêu cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất?

Trả lời: phải thả 12 con cá

Ông Nam cần xây dựng một bể chứa nước có dạng hình hộp chữ nhật không có nắp đậy để phục vụ cho việc tưới cây trong vườn. Do các điều kiện về diện tích vườn, ông Nam cần bể có thể tích là $36 m^3$ , đáy bể có chiều dài gấp hai lần chiều rộng và chiều rộng không quá $4 m$ , biết rằng chi phí vật liệu xây dựng mỗi mét vuông diện tích bề mặt là như nhau. Hỏi chiều cao bể nước bằng bao nhiêu để tổng chi phí vật liệu là nhỏ nhất?

Trả lời:  cần xây bể có chiều cao là $2 \left(m\right)$ .

Ông \(A\) dự định sử dụng hết \(5\,{{\rm{m}}^{\rm{2}}}\) kính để làm bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng. Bể cá có thể tích lớn nhất bằng bao nhiêu?

Trả lời: \(1,01\,{{\rm{m}}^{\rm{3}}}\).

Một chất điểm chuyển động theo phương trình \(S =  - {t^3} + 9{t^2} + t + 10\) trong đó \(t\) tính bằng \(\left( s \right)\) và \(S\) tính bằng \(\left( m \right)\). Thời gian để vận tốc của chất điểm đạt giá trị lớn nhất là

Trả lời: \(t = 3s\).

Một vật chuyển động theo quy luật \(s =  - 2{t^3} + 24{t^2} + 9t - 3\) với \(t\) là khoảng thời gian tính từ lúc bắt đầu chuyển động và \(s\) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?

Trả lời: 105 \(\left( {m/s} \right)\)

Một chất điểm chuyển động theo quy luật \(s =  - {t^3} + 6{t^2} + 17t\), với \(t\) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và \(s\) là quãng đường vật đi được trong khoảng thời gian đó. Khi đó vận tốc \(v\,\left( {m/s} \right)\)của chuyển động đạt giá trị lớn nhất trong khoảng \(8\) giây đầu tiên bằng

Trả lời: \(29\,m/s\).       

Một chất điểm chuyển động theo phương trình \[S =  - {t^3} + 3{t^2} - 2\], trong đó \[t\] tính bằng giây và \[S\] tính theo mét. Chuyển động có vận tốc lớn nhất là

Trả lời: \[3\] m/s.           

Ông \[A\] dự định sử dụng hết \[6,5\,{{\rm{m}}^2}\] kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?

Trả lời: \[1,50\,{{\rm{m}}^3}\].

Một ông nông dân có \(2400\)m hàng rào và muốn rào lại cánh đồng hình chữ nhật tiếp giáp với một con sông. Ông không cần rào cho phía giáp bờ sông. Hỏi ông có thể rào được cánh đồng với diện tích lớn nhất là bao nhiêu?

Trả lời: \(720000\)m2.    

Tìm \(m\) để tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( x \right) = {x^4} - 2{x^2} + m\) trên đoạn \(\left[ { - 1;1} \right]\) bằng 5.

Trả lời: \(m = 3\).           

Ông An muốn xây một bể chứa nước dạng hình hộp chữ nhật, phần nắp trên ông để trống một ô có diện tích bằng \(20\% \) diện tích của đáy bể. Biết đáy bể là một hình chữ nhật có chiều dài gấp đôi chiều rộng, biết bể có thể chứa tối đa \(10{m^3}\) nước và giá tiền thuê nhân công là \(500000\) đồng\(/{m^2}\). Số tiền trả ít nhất cho nhân công mà ông phải trả gần nhất với số nào sau đây?

Trả lời: \[14\] triệu đồng.              

Người ta giăng lưới để nuôi riêng một loại cá trên một góc hồ. Biết rằng lưới được giăng theo một đường thẳng từ một vị trí trên bờ ngang đến một vị trí trên bờ dọc và phải đi qua một cái cọc đã cắm sẵn ở vị trí \(A\). Hỏi diện tích nhỏ nhất có thể giăng là bao nhiêu, biết rằng khoảng cách từ cọc đến bờ ngang là \(5\,m\) và khoảng cách từ cọc đến bờ dọc là \(12\,m\).

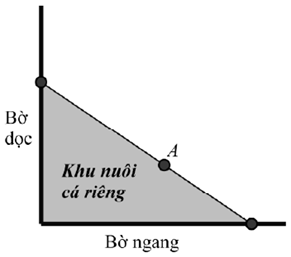Trả lời: \(120{m^2}\).

Ông \(A\) dự định sử dụng hết \(6,7{\mkern 1mu} {m^2}\) kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng. Bể cá có dung tích lớn nhất bằng bao nhiêu?

Trả lời:……………………………….