40 bài tập Một số bài toán thực tế liên quan đến GTLN, GTNN của hàm số (có lời giải)
40 câu hỏi
Hình vẽ bên dưới cho biết sự thay đổi của nhiệt độ ở một thành phố trong một ngày.
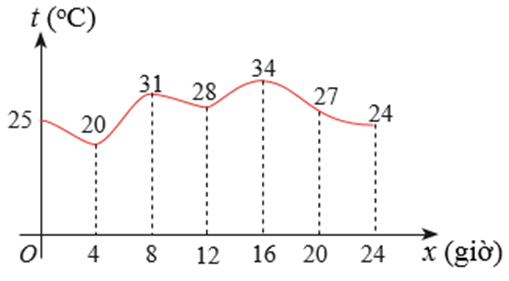
Khẳng định nào sau đây đúng? Vì sao?
i) Nhiệt độ cao nhất trong ngày là 28oC.
ii) Nhiệt độ cao nhất trong ngày là 40oC.
iii) Nhiệt độ cao nhất trong ngày là 34oC.
a) Hãy xác định thời điểm có nhiệt độ cao nhất trong ngày.
b) Nhiệt độ thấp nhất trong ngày là bao nhiêu?
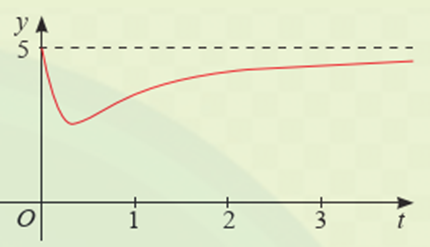
Sự phân huỷ của rác thải hữu cơ y có trong nước sẽ làm tiêu hao oxygen hoà tan trong nước. Nồng độ oxygen (mg/l) trong một hồ nước sau t giờ (t ≥ 0) khi một lượng rác thải hữu cơ bị xả vào hồ được xấp xỉ bởi hàm số: \[y\left( t \right) = 5 - \frac{{15t}}{{9{t^2} + 1}}\]. Vào các thời điểm nào nồng độ oxygen trong nước cao nhất và thấp nhất?
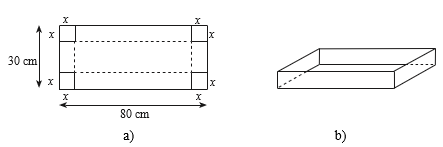
Từ một tấm bìa hình chữ nhật có chiều rộng 30 cm và chiều dài 80 cm (Hình 4a), người ta cắt ở bốn góc bốn hình vuông có cạnh x (cm) với 5 ≤ x ≤ 10 và gấp lại để tạo thành chiếc hộp có dạng hình hộp chữ nhật không nắp như Hình 4b. Tìm x để thể tích chiếc hộp là lớn nhất (kết quả làm tròn đến hàng phần trăm).
Tam giác vuông có cạnh huyền bằng 5 cm có thể có diện tích lớn nhất bằng bao nhiêu?
Trong các hình chữ nhật có chu vi là 24 cm, hãy tìm hình chữ nhật có diện tích lớn nhất
Tìm hai số không âm a và b có tổng bằng 10 sao cho:
Biểu thức ab đạt giá trị lớn nhất
Tìm hai số không âm a và b có tổng bằng 10 sao cho:
Tổng bình phương của chúng đạt giá trị nhỏ nhất;
Tìm hai số không âm a và b có tổng bằng 10 sao cho:
Biểu thức ab2 đạt giá trị lớn nhất
Tính diện tích lớn nhất \({S_{\max }}\) của một hình chữ nhật nội tiếp trong nửa đường tròn bán kính \(R = 6\,{\rm{cm}}\) nếu một cạnh của hình chữ nhật nằm dọc theo đường kính của hình tròn mà hình chữ nhật đó nội tiếp.
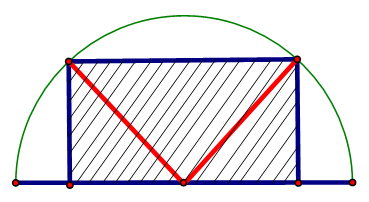
Khi làm nhà kho, bác An muốn cửa sổ có dạng hình chữ nhật với chu vi bằng 4 m (Hình vẽ). Tìm kích thước khung cửa sổ sao cho diện tích cửa sổ lớn nhất (để hứng được nhiều ánh sáng nhất)?
Khối lượng q (kg) của một mặt hàng mà cửa tiệm bán được trong một ngày phụ thuộc vào giá bán p (nghìn đồng/kg) theo công thức p=15 − \[\frac{1}{2}\]q. Doanh thu từ việc bán mặt hàng trên của cửa tiệm được tính theo công thức R = pq.
a) Viết công thức biểu diễn R theo p.
b) Tìm giá bán mỗi kilôgam sản phẩm để đạt được doanh thu cao nhất và xác định doanh thu cao nhất đó.
Hộp sữa 1 l được thiết kế dạng hình hộp chữ nhật với đáy là hình vuông cạnh x cm. Tìm x để diện tích toàn phần của hộp nhỏ nhất.
Trong 5 giây đầu tiên, một chất điểm chuyển động theo phương trình \[s(t) = - {t^3} + 6{t^2} + t + 5\] trong đó t tính bằng giây và s tính bằng mét. Chất điểm có vận tốc tức thời lớn nhất bằng bao nhiêu trong 5 giây đầu tiên đó?
Một vật chuyển động theo quy luật \(s = \frac{1}{3}{t^3} - {t^2} + 9t,\)với \[t\](giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và \[s\] (mét) là quãng đường vật đi được trong thời gian đó. Hỏi trong khoảng thời gian \(10\) giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
Một vật chuyển động theo quy luật \(S = 10{t^2} - \frac{1}{3}{t^3}\), với t (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và là quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian \(15\) giây từ lúc vật bắt đầu chuyển động vận tốc \(v\left( {m/s} \right)\) của vật đạt giá trị lớn nhất tại thời điểm \(t\left( s \right)\) bằng:
Một chất điểm chuyển động theo quy luật \(S\left( t \right) = 1 + 3{t^2} - {t^3}\). Vận tốc của chuyển động đạt giá trị lớn nhất khi t bằng bao nhiêu:
Một chất điểm chuyển động có phương trình chuyển động là \[s = - {t^3} + 6{t^2} + 17t\], với \[t\left( s \right)\] là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và \[s\left( m \right)\] là quãng đường vật đi được trong khoảng thời gian đó. Trong khoảng thời gian 8 giây đầu tiên, vận tốc \[v\left( {m/s} \right)\]của chất điểm đạt giá trị lớn nhất bằng
Một chất điểm chuyển động theo phương trình \[S = - {t^3} + 3{t^2} - 2\], trong đó \[t\] tính bằng giây và \[S\] tính theo mét. Chuyển động có vận tốc lớn nhất là
Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong \(t\) giờ được tính theo công thức \(c\left( t \right) = \frac{t}{{{t^2} + 1}}\) (mg/L). Sau khi tiêm thuốc bao lâu thì nồng độ thuốc trong máu của bệnh nhân cao nhất?
Độ giảm huyết áp của một bệnh nhân được cho bởi công thức \(G\left( x \right) = 0,035{x^2}\left( {15 - x} \right)\), trong đó \(x\) là liều lượng thuốc được tiêm cho bệnh nhân (\(x\) được tính bằng miligam). Tính liều lượng thuốc cần tiêm (đơn vị miligam) cho bệnh nhân để huyết áp giảm nhiều nhất.
Người ta bơm xăng vào bình xăng của một xe ô tô. Biết rằng thể tích V (lít) của lượng xăng trong bình xăng tính theo thời gian bơm xăng 1 (phút) được cho bởi công thức \[V(t) = 300\left( {{t^2} - {t^3}} \right) + 4\] với 0 ≤ t ≤ 0,5. (Nguồn: R.I. Charles et al., Algebra 2, Pearson)
a) Ban đầu trong bình xăng có bao nhiêu lít xăng?
b) Sau khi bơm 30 giây thì bình xăng đầy. Hỏi dung tích của bình xăng trong xe là bao nhiêu lít?
c) Khi xăng chảy vào bình xăng, gọi V'(t) là tốc độ tăng thể tích tại thời điểm t với 0≤ t ≤0,5. Xăng chảy vào bình xăng ở thời điểm nào có tốc độ tăng thể tích là lớn nhất?
Giả sử chi phí tiền xăng C (đồng) phụ thuộc tốc độ trung bình \(v(\;{\rm{km}}/{\rm{h}})\) theo công thức:
\(C(v) = \frac{{16000}}{v} + \frac{5}{2}v(0 < v \le 120)\)
Để biểu diễn trực quan sự thay đổi của \(C(v)\) theo \(v\), người ta đã vẽ đổ thị hàm số \(C(v)\) như hình bên dưới.
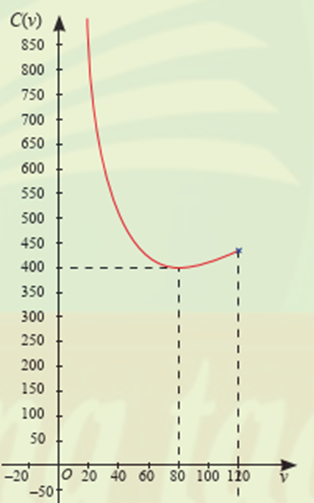
a) Khảo sát và vẽ đồ thị hàm số \(C(v)\) trên \((0;120]\).
b) Tài xế xe tải lái xe với tốc độ trung bình là bao nhiêu để tiết kiệm tiền xăng nhất?
Ho ép khí quản co lại, ảnh hưởng đến tốc độ của không khí đi vào khí quản. Tốc độ của không khí đi vào khí quản khi họ được cho bởi công thức: V = k(R-r)r2 vôi 0 ≤ r <R, trong đó k là hằng số, R là bán kính bình thường của khí quản, r là bán kính khí quản khi ho (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014). Hỏi bán kính của khí quản khi ho bằng bao nhiêu thì tốc độ của không khí đi vào khí quản là lớn nhất?
Một trang sách có dạng hình chữ nhật với diện tích là 384 cm2. Sau khi để lề trên và lề dưới đều là 3 cm, để lề trái và lề phải đều là 2 cm. Phần còn lại của trang sách được in chữ. Kích thước tối ưu của trang sách là bao nhiêu để phần in chữ trên trang sách có diện tích lớn nhất?
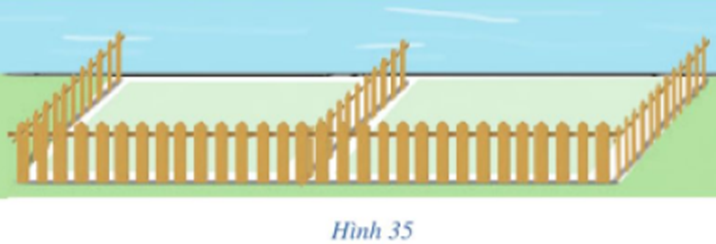
Một người nông dân có 15 000 000 đồng để làm một hàng rào hình chữ E dọc theo một con sông bao quanh hai khu đất trồng rau có dạng hai hình chữ nhật bằng nhau (Hình 35). Đối với mặt hàng rào song song với bờ sông thì chi phí nguyên vật liệu là 60 000 đồng/mét, còn đối với ba mặt hàng rào song song nhau thì chi phí nguyên vật liệu là 50 000 đồng/mét, mặt giáp với bờ sông không phải rào. Tìm diện tích lớn nhất của hai khu đất thu được sau khi làm hàng rào.
Một bác nông dân có ba tấm lưới thép B40, mỗi tấm dài a (m) và muốn rào một mảnh vườn dọc bờ sông có dạng hình thang cân ABCD như Hình 36 (bờ sông là đường thẳng CD không phải rào). Hỏi bác đó có thể rào được mảnh vườn có diện tích lớn nhất là bao nhiêu mét vuông?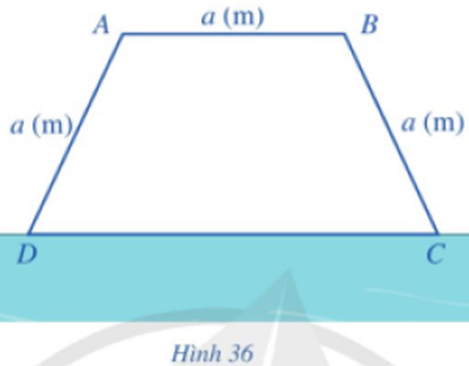
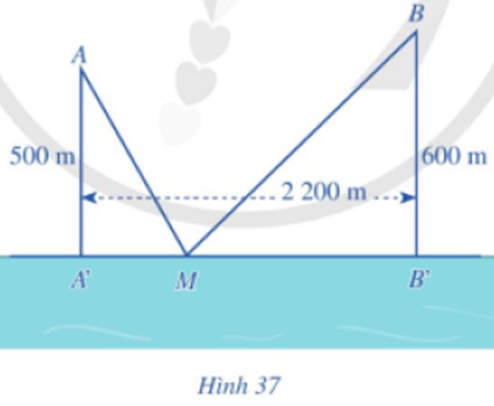
Có hai xã A, B cùng ở một bên bờ sông Lam, khoảng cách từ hai xã đó đến bờ sông lần lượt là AA’ = 500 m, BB’ = 600 m và người ta đo được A'B' = 2200 m (Hình 37). Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Để tiết kiệm chi phí, các kĩ sư cần phải chọn vị trí M của trạm cung cấp nước sạch đó trên đoạn A’B' sao cho tổng khoảng cách từ hai xã đến vị trí M là nhỏ nhất. Hãy tìm giá trị nhỏ nhất của tổng khoảng cách đó.
Một công ty kinh doanh bất động sản có 20 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá 2 triệu đồng/1 tháng thì tất cả các căn hộ đều có người thuê. Nhưng cứ mỗi lần tăng giá cho thuê mỗi căn hộ thêm 200 nghìn đồng/1 tháng thì có thêm một căn hộ bị bỏ trống. Hỏi công ty nên cho thuê mỗi căn hộ bao nhiêu tiền một tháng để tổng số tiền thu được là lớn nhất?
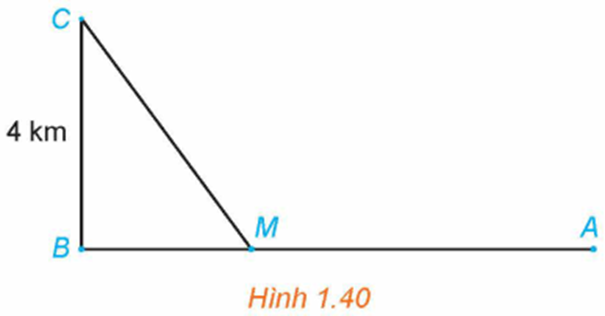
Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở C như Hình 1.40. Khoảng cách từ C đến B là 4 km. Bờ biển chạy thẳng từ A đến B với khoảng cách là 10 km. Tổng chi phí lắp đặt cho 1 km dãy điện trên biển là 50 triệu đồng, còn trên đất liền là 30 triệu đồng. Xác định vị trí điểm M trên đoạn AB (điểm nổi dây từ đất liền ra đảo) để tổng chi phí lắp đặt là nhỏ nhất.
Giả sử sự lây lan của một loại virus ở một địa phương có thể được mô hình hoa bằng hàm số \[N(t) = - {t^3} + 12{t^2},0 \le t \le 12\], trong đó N là số người bị nhiễm bệnh (tính bằng trăm người) và t là thời gian (tuần).
a) Hãy ước tính số người tối đa bị nhiễm bệnh ở địa phương đó.
b) Đạo hàm N'(t) biểu thị tốc độ lây lan của virus (còn gọi là tốc độ truyền bệnh). Hỏi virus sẽ lây lan nhanh nhất khi nào?
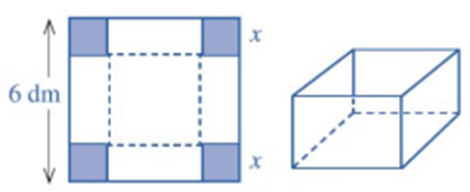
Cho một tấm nhôm có dạng hình vuông cạnh 6 dm. Bác Ánh cắt ở bốn góc bốn hình vuông cùng có độ dài x (dm), rồi gập tấm nhôm lại như hình vẽ bên dưới để được một cái hộp có dạng khối hộp chữ nhật không có nắp. Gọi V là thể tích của khối hộp đó tính theo x. Tìm x (dm) để khối hộp tạo thành có thể tích lớn nhất.
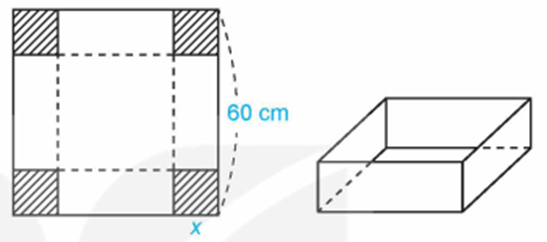
Từ một tấm bìa carton hình vuông có độ dài cạnh bằng 60 cm, người ta cắt bốn hình vuông bằng nhau ở bốn góc rồi gập thành một chiếc hộp có dạng hình hộp chữ nhật không có nắp (Hình vẽ). Tính cạnh của các hình vuông bị cắt sao cho thể tích của chiếc hộp là lớn nhất.
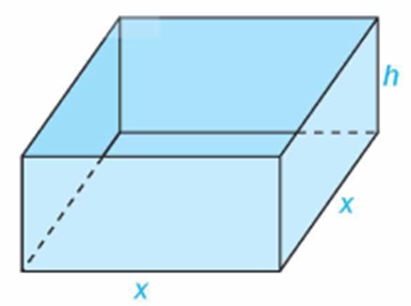
Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng 108 cm2 như Hình vẽ. Tìm các kích thước của chiếc hộp sao cho thể tích của hộp là lớn nhất.
Một nhà sản xuất cần làm ra những chiếc bình có dạng hình trụ với dung tích 1000 cm3. Mặt trên và mặt dưới của bình được làm bằng vật liệu có giá 1,2 nghìn đồng/cm2, trong khi mặt bên của bình được làm bằng vật liệu có giá 0,75 nghìn đồng/cm2. Tìm các kích thước của bình để chi phí vật liệu sản xuất mỗi chiếc bình là nhỏ nhất.
Ông Nam cần xây dựng một bể chứa nước có dạng hình hộp chữ nhật không có nắp đậy để phục vụ cho việc tưới cây trong vườn. Do các điều kiện về diện tích vườn, ông Nam cần bể có thể tích là 36 m3, đáy bể có chiều dài gấp hai lần chiều rộng và chiều rộng không quá 4 m, biết rằng chi phí vật liệu xây dựng mỗi mét vuông diện tích bề mặt là như nhau. Hỏi chiều cao bể nước bằng bao nhiêu để tổng chi phí vật liệu là nhỏ nhất?
Trong một thí nghiệm y học, người ta cấy 1000 vi khuẩn vào môi trường dinh dưỡng. Bằng thực nghiệm, người ta xác định được số lượng vi khuẩn thay đổi theo thời gian bởi công thức:\[N(t) = 1000 + \frac{{100t}}{{100 + {t^2}}}(con),\]trong đó t là thời gian tính bằng giây (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014). Tính số lượng vi khuẩn lớn nhất kể từ khi thực hiện cấy vi khuẩn vào môi trường dinh dưỡng.
Cho một hình trụ nội tiếp trong hình nón có chiều cao bằng 12 cm và bán kính đáy bằng 5 cm (Hình 4a). Người ta cắt hình nón, trụ này theo mặt phẳng chứa đường thẳng nối đỉnh và tâm hình tròn đáy của hình nón thì thu được một hình phẳng như Hình 4b.
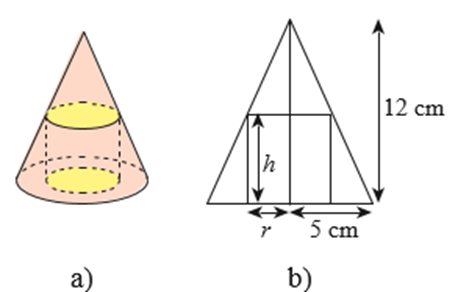
a) Chứng minh rằng công thức tính bán kính r của đáy hình trụ theo chiều cao h của nó là: \[r = \frac{{5\left( {12 - h} \right)}}{{12}}\]
b) Chứng minh biểu thức sau biểu thị thể tích khối trụ theo h: \[V(h) = \frac{{25\pi h{{(12 - h)}^2}}}{{144}}\]
c) Tìm h để khối trụ có thể tích lớn nhất.
Một doanh nghiệp sản xuất độc quyền một loại sản phẩm. Giả sử khi sản xuất và bán hết x sản phẩm đó (0 < x ≤2000), tổng số tiền doanh nghiệp thu được (đơn vị: chục nghìn đồng) là f (x) = 2 000x – x2 và tổng chi phí (đơn vị: chục nghìn đồng) doanh nghiệp chỉ ra là g(x) = x2 + 1 440x + 50. Giả sử mức thuế phụ thu trên một đơn vị sản phẩm bán được là t (chục nghìn đồng) (0<t<300). Tìm mức thuế phụ thu t (trên một đơn vị sản phẩm) sao cho nhà nước nhận được số tiền thuế phụ thu lớn nhất và doanh nghiệp cũng thu được lợi nhuận lớn nhất theo mức thuế phụ thu đó (Nguồn: Nguyễn Huy Hoàng (Chủ biên), Hướng dẫn giải bài tập Toán Cao cấp cho các nhà kinh tế, phần 2: Giải tích toán học, Nhà xuất bản Thống kê 2007).
Một hồ nược nhân tạo được xây dựng trong một công viên giải trí. Trong mô hình minh hoạ (Hình vẽ), nó được giối hạn bởi các trục toạ độ và đồ thị của hàm số \(y = f(x) = \frac{1}{{10}}\left( { - {x^3} + 9{x^2} - 15x + 56} \right)\). Đơn vị đo độ dài trên mỗi trục tọa độ là \(100\;{\rm{m}}\)
(Nguồn: \({\rm{A}}\). Bigalke et al, Mathematik, Grundkurs ma-1, Cornelsen 2010).
a) Đường dạo ven hổ chạy dọc theo trục Ox dài bao nhiêu mét?
b) Tại những điểm nào trên đường đi dạo ven hồ (chạy dọc theo trục Ox) thì khoảng cách theo phương thẳng đứng đến bờ hổ đối diện là lôn nhất? Tìm khoảng cách lớn nhất đó.
c) Trong công viên có một con đường chạy dọc theo đồ thị hàm số \(y = - 1,5x + 18\). Người ta dự định xây dựng bên bờ hổ một bến thuyền đạp nước sao cho khoảng cách từ bến thuyển đến con đường này là ngắn nhất. Tìm tọ̣a độ của điểm để xây bến thuyền này.
Khi một vật lạ mắc kẹt trong khí quản khiến ta phải ho, cơ hoành đẩy lên trên gây ra tăng áp lực trong phổi, theo đó cuống họng co thắt làm hẹp khí quản khiến không khí đi qua mạnh hơn. Đối với một lượng không khí bị đẩy ra trong một khoảng thời gian cố định, khí quản càng nhỏ thì luồng không khí càng đẩy ra nhanh hơn. Vận tốc luồng khí thoát ra càng cao, lực tác động lên vật lạ càng lớn. Qua nghiên cứu một số trường hợp, người ta nhận thấy vận tốc \(v\) của luồng khí liên hệ với bán kính \(x\) của khí quản theo công thức: \(v(x) = k\left( {{x_0} - x} \right){x^2}{\rm{ v?i }}\frac{1}{2}{x_0} \le x \le {x_0},\)trong đó \(k\) là hằng số \((k > 0)\) và \({x_0}\) là bán kính khí quản ở trạng thái bình thường. Tìm \(x\) theo \({x_0}\) để vận tốc của luồng khí một cơn ho trong trường hợp này là lớn nhất. (Nguồn: James Stewart, J. (2015). Calculus. Cengage Learning 8th edition, p.285)








