(Trả lời ngắn) 26 bài tập Tích phân (có lời giải)

Một ô tô đang chạy với tốc độ \[20\left( {m/s} \right)\] thì gặp chướng ngại vật, người lái đạp phanh, từ thời điểm đó ô tô chuyển động chậm dần đều với vận tốc \[v\left( t \right) =  - 5t + 20\left( {m/s} \right)\], trong đó \[t\] là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét (\[m\])?

Trả lời:……………………………..

Một chất điểm \(A\) xuất phát từ \(O\), chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật \(v\left( t \right) = \frac{1}{{120}}{t^2} + \frac{{58}}{{45}}t\left( {m/s} \right)\), trong đó \(t\) (giây) là khoảng thời gian tính từ lúc \(A\) bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm \(B\) cũng xuất phát từ \(O\), chuyển động thẳng cùng hướng với \(A\) nhưng chậm hơn \(3\) giây so với \(A\) và có gia tốc bằng \(a\left( {m/{s^2}} \right)\) (\(a\) là hằng số). Sau khi \(B\) xuất phát được \(15\) giây thì đuổi kịp \(A\). Vận tốc của \(B\) tại thời điểm đuổi kịp \(A\) bằng

Trả lời:……………………………..

Một chất điểm \(A\) xuất phát từ \(O\), chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật \(v\left( t \right) = \frac{1}{{150}}{t^2} + \frac{{59}}{{75}}t\left( {m/s} \right)\), trong đó \(t\)(giây) là khoảng thời gian tính từ lúc \(a\) bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm \(B\) cũng xuất phát từ \(O\), chuyển động thẳng cùng hướng với \(A\) nhưng chậm hơn 3 giây so với \(A\) và có gia tốc bằng \(a\left( {m/{s^2}} \right)\)(\(a\) là hằng số). Sau khi \(B\) xuất phát được 12 giây thì đuổi kịp \(A\). Vận tốc của \(B\) tại thời điểm đuổi kịp \(A\) bằng

Trả lời:……………………………..

Một ô tô bắt đầu chuyển động thẳng đều với vận tốc \({v_0}\), sau 6 giây chuyển động thì gặp chướng ngại vật nên bắt đầu giảm tốc độ với vận tốc chuyển động \(v(t) =  - \frac{5}{2}t + a\,\,(m/s),\,\,(t \ge 6)\) cho đến khi dừng hẳn. Biết rằng kể từ lúc chuyển động đến lúc dừng thì ô tô đi được quãng đường là 80m. Tìm \({v_0}\).

Trả lời:……………………………..

 Để đảm bảo an toàn khi lưu thông trên đường, các xe ô tô khi dừng đèn đỏ phải cách nhau tối thiểu \(1\,{\rm{m}}\). Một ô tô \(A\) đang chạy với vận tốc \[16\,{\rm{m/s}}\] bỗng gặp ô tô \(B\) đang dừng đèn đỏ nên ô tô \(A\) hãm phanh và chuyển động chậm dần đều với vận tốc được biểu thị bởi công thức \({v_A}\left( t \right) = 16 - 4t\) (đơn vị tính bằng \[{\rm{m/s}}\]), thời gian tính bằng giây. Hỏi rằng để có \(2\) ô tô \(A\) và \(B\) đạt khoảng cách an toàn khi dừng lại thì ô tô \(A\) phải hãm phanh khi cách ô tô \(B\) một khoảng ít nhất là bao nhiêu?

Trả lời:……………………………..

Một chất điểm đang chuyển động với vận tốc \({v_0} = 15\;{\rm{m/s}}\) thì tăng tốc với gia tốc \(a\left( t \right) = {t^2} + 4t\;\left( {{\rm{m/}}{{\rm{s}}^2}} \right)\). Tính quãng đường chất điểm đó đi được trong khoảng thời gian \(3\) giây kể từ lúc bắt đầu tăng vận tốc.

Trả lời:……………………………..

Một vật chuyển động với vận tốc \(10\,{\rm{m/s}}\) thì tăng tốc với gia tốc được tính theo thời gian là \(a\left( t \right) = {t^2} + 3t\). Tính quãng đường vật đi được trong khoảng thời gian \(6\) giây kể từ khi vật bắt đầu tăng tốc.

Trả lời:……………………………..

Một chiếc máy bay chuyển động trên đường băng với vận tốc \(v\left( t \right) = {t^2} + 10t\) \(\left( {m/s} \right)\) với \(t\) là thời gian được tính theo đơn vị giây kể từ khi máy bay bắt đầu chuyển động. Biết khi máy bay đạt vận tốc \(200\,\left( {m/s} \right)\) thì rời đường băng. Quãng đường máy bay đã di chuyển trên đường băng là

Trả lời:……………………………..

Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc \({v_1}\left( t \right) = 7t{\rm{ }}\left( {m/s} \right)\). Đi được \[5{\rm{s}}\], người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc \(a =  - 70{\rm{  }}\left( {m/{s^2}} \right)\). Tính quãng đường \[S\] đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn.

Trả lời:……………………………..

Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc \({v_1}\left( t \right) = 2t\,\,\left( {{\rm{m/s}}} \right)\). Đi được \(12\) giây, người lái xe gặp chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc \(a =  - 12\,\left( {{\rm{m/}}{{\rm{s}}^2}} \right)\). Tính quãng đường \(s\left( {\rm{m}} \right)\) đi được của ôtô từ lúc bắt đầu chuyển động đến khi dừng hẳn?

Trả lời:……………………………..

Một ôtô đang dừng và bắt đầu chuyển động theo một đường thẳng với gia tốc \(a\left( t \right) = 6 - 2t\,\,\left( {m/{s^2}} \right)\), trong đó \[t\] là khoảng thời gian tính bằng giây kể từ lúc ôtô bắt đầu chuyển động. Hỏi quảng đường ôtô đi được từ lúc bắt đầu chuyển động đến khi vận tốc của ôtô đạt giá trị lớn nhất là bao nhiêu mét?

Trả lời:……………………………..

Một chất điểm \(A\) xuất phát từ \(O\), chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật \(v(t) = \frac{1}{{180}}{t^2} + \frac{{11}}{{18}}t\,\left( {m/s} \right)\), trong đó \(t\) (giây) là khoảng thời gian tính từ lúc \(A\) bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm \(B\) cũng xuất phát từ \(O\), chuyển động thẳng cùng hướng với \(A\) nhưng chậm hơn \(5\) giây so với \(A\) và có gia tốc bằng \(a\,\left( {m/{s^2}} \right)\) (\(a\) là hằng số). Sau khi \(B\) xuất phát được \(10\) giây thì đuổi kịp \(A\). Vận tốc của \(B\) tại thời điểm đuổi kịp \(A\) bằng

Trả lời:……………………………..

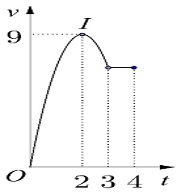
Một vật chuyển động trong \[3\] giờ với vận tốc \[v\left( {{\rm{km/h}}} \right)\] phụ thuộc thời gian \[t{\rm{ }}\left( {\rm{h}} \right)\]có đồ thị là một phần của đường parabol có đỉnh \[I\left( {2;9} \right)\] và trục đối xứng song song với trục tung như hình bên. Tính quãng đường \[s\] mà vật di chuyển được trong \[3\] giờ đó.

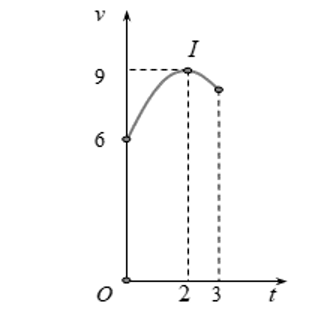
Trả lời:……………………………..

Một vật chuyển động trong 3 giờ với vận tốc \(v(km/h)\) phụ thuộc vào thời gian \(t(h)\) có đồ thị vận tốc như hình bên. Trong thời gian 1 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường parabol có đỉnh \(I(2;9)\) và trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường \(s\) mà vật chuyển động được trong 3 giờ đó (kết quả làm tròn đến hàng phần trăm).

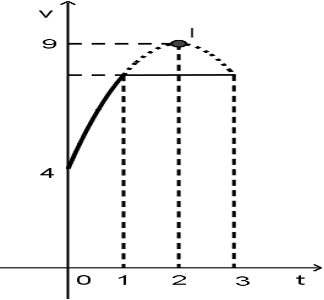
Trả lời:……………………………..

Một người chạy trong 2 giờ, vận tốc v (km/h) phụ thuộc vào thời gian t (h) có đồ thị là 1 phần của đường Parabol với đỉnh \(I\left( {1;5} \right)\) và trục đối xứng song song với trục tung Ov như hình vẽ. Tính quảng đường S người đó chạy được trong 1 giờ 30 phút kể từ lúc bắt đầu chạy (kết quả làm tròn đến 2 chữ số thập phân).

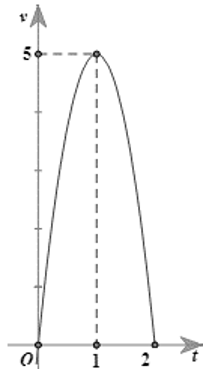
Trả lời:……………………………..

Một ô tô đang chạy với vận tốc là 12 \[\left( {m/s} \right)\] thì người lái đạp phanh; từ thời điểm đó ô tô chuyển động chậm dần đều với vận tốc \(v\left( t \right) =  - 6t + 12\) \[\left( {m/s} \right)\], trong đó \(t\) là khoảng thời gian tính bằng giây kể từ lúc đạp phanh. Hỏi từ lúc đạp phanh đến lúc ô tô dừng hẳn, ô tô còn di chuyển được bao nhiêu mét?

Trả lời:……………………………..

Một ô tô đang chạy với vận tốc 10m/s thì người lái đạp phanh; từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc \(v\left( t \right) =  - 5t + 10\) (m/s), trong đó \(t\) là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét?

Trả lời:……………………………..

Một chất điểm \(A\) xuất phát từ \(O\), chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật \(v\left( t \right) = \frac{1}{{100}}{t^2} + \frac{{13}}{{30}}t \left( {{\rm{m/s}}} \right)\), trong đó \(t\) (giây) là khoảng thời gian tính từ lúc \(A\) bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm \(B\) cũng xuất phát từ \(O\), chuyển động thẳng cùng hướng với \(A\) nhưng chậm hơn \(10\) giây so với \(A\) và có gia tốc bằng \(a \left( {{\rm{m/}}{{\rm{s}}^2}} \right)\) (\(a\) là hằng số). Sau khi \(B\) xuất phát được \(15\) giây thì đuổi kịp \(A\). Vận tốc của \(B\) tại thời điểm đuổi kịp \(A\) bằng bao nhiêu?

Trả lời:……………………………..

Một ô tô chuyển động nhanh dần đều với vận tốc \(v\left( t \right) = 7t\) \(\left( {{\rm{m/s}}} \right)\). Đi được \(5\)\(\left( {\rm{s}} \right)\) người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc \(a =  - 35\) \(\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\). Tính quãng đường của ô tô đi được từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn?

Trả lời:……………………………..

Một người chạy trong thời gian 1 giờ, vận tốc \(v\) (km/h) phụ thuộc vào thời gian \(t\) (h) có đồ thị là một phần parabol với đỉnh \(I\left( {\frac{1}{2};{\rm{ }}8} \right)\) và trục đối xứng song song với trục tung như hình bên. Tính quảng đường \(s\) người đó chạy được trong khoảng thời gian \(45\) phút, kể từ khi chạy?

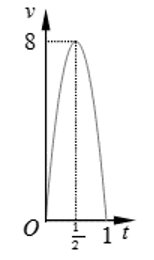
Trả lời:……………………………..

Một vật chuyển động trong 4 giờ với vận tốc \(v\) (km/h) phụ thuộc thời gian \(t\) (h) có đồ thị của vận tốc như hình bên. Trong khoảng thời gian \(3\) giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường parabol có đỉnh \(I\left( {2;\;9} \right)\) với trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường \(s\) mà vật di chuyển được trong \(4\) giờ đó.

Trả lời:……………………………..

 Một vật chuyển động trong 6 giờ với vận tốc \[v\left( {km/h} \right)\]phụ thuộc vào thời gian \[t\left( h \right)\]có đồ thị như hình bên dưới. Trong khoảng thời gian 2 giờ từ khi bắt đầu chuyển động, đồ thị là một phần đường Parabol có đỉnh \[I\left( {3;9} \right)\]và có trục đối xứng song song với trục tung. Khoảng thời gian còn lại, đồ thị vận tốc là một đường thẳng có hệ số góc bằng \[\frac{1}{4}\]. Tính quảng đường \[s\]mà vật di chuyển được trong 6 giờ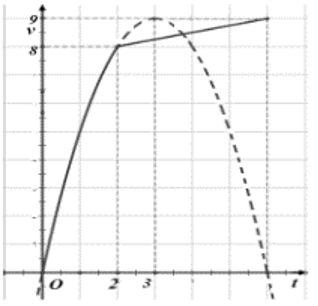Trả lời:……………………………..

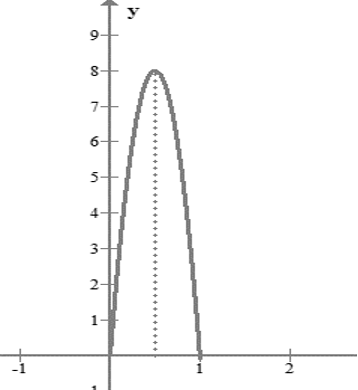
Một người chạy trong thời gian \(1\) giờ, với vận tốc \(v\) \(\left( {{\rm{km/h}}} \right)\) phụ thuộc vào thời gian \(t\left( {\rm{h}} \right)\) có đồ thị là một phần của parabol có đỉnh \(I\left( {\frac{1}{2};8} \right)\) và trục đối xứng song song với trục tung như hình vẽ. Tính quãng đường \[{\rm{S}}\] người đó chạy được trong thời gian \(45\) phút, kể từ khi bắt đầu chạy.

Trả lời:……………………………..

Một vật chuyển động trong \[4\] giờ với vận tốc \(v\,\,(km/h)\) phụ thuộc thời gian \(t\,\,(h)\) có đồ thị là một phần của đường parabol có đỉnh \(I(1;\,1)\) và trục đối xứng song song với trục tung như hình bên. Tính quãng đường \(s\) mà vật di chuyển được trong \[4\] giờ kể từ lúc xuất phát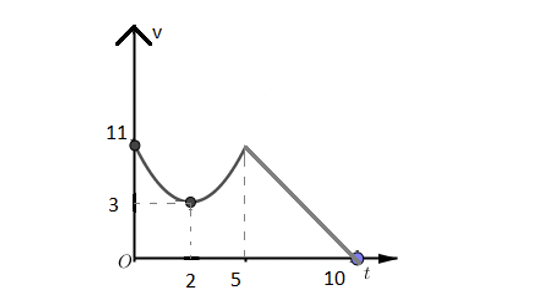

Trả lời:……………………………..

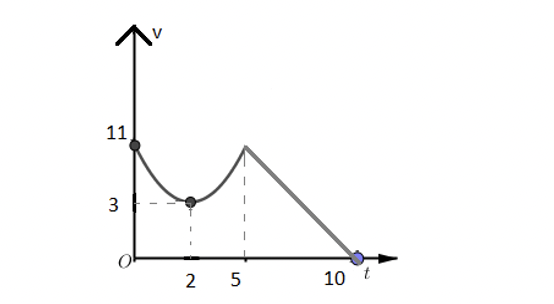
   Chất điểm chuyển động theo quy luật vận tốc \[v\left( t \right)\left( {m/s} \right)\] có dạng đường Parapol khi \[0 \le t \le 5\left( s \right)\] và \[v\left( t \right)\] có dạng đường thẳng khi \[5 \le t \le 10\left( s \right)\].Cho đỉnh Parapol là \[I\left( {2,3} \right)\]. Hỏi quãng đường đi được chất điểm trong thời gian \[0 \le t \le 10\left( s \right)\] là bao nhiêu mét?

Trả lời:……………………………..