22 câu trắc nghiệm Toán 12 Chân trời sáng tạo Bài 2. Tích phân (Đúng sai - Trả lời ngắn) có đáp án
22 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Biết \(\int\limits_1^2 {f\left( x \right)dx} = 2\). Khi đó \(\int\limits_1^2 {2f\left( x \right)dx} \) bằng
2.
−4.
4.
−2.
Biết \(\int\limits_1^2 {f\left( x \right)dx} = 2\) và \(\int\limits_1^2 {g\left( x \right)dx} = 6\). Khi đó, \(\int\limits_1^2 {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} \) bằng
−4.
8.
4.
−8.
Cho hàm số \(f\left( x \right)\) có đạo hàm trên đoạn \(\left[ {1;2} \right],f\left( 1 \right) = 1\) và \(\int\limits_1^2 {f'\left( x \right)dx} = 5\). Giá trị \(f\left( 2 \right)\) bằng
6.
4.
3.
7.
Giả sử f là hàm số liên tục trên khoảng K và a, b, c là các số bất kỳ trên khoảng K. Khẳng định nào sau đây sai?
\(\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^b {f\left( t \right)dt} \).
\(\int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)} dx = \int\limits_a^b {f\left( x \right)dx} \).
\(\int\limits_a^a {f\left( x \right)dx} = 1\).
\(\int\limits_a^b {f\left( x \right)dx} = - \int\limits_b^a {f\left( x \right)dx} \).
Cho \(\int\limits_0^2 {f\left( x \right)dx} = 5\) và \(\int\limits_0^5 {f\left( x \right)dx} = - 3\), khi đó \(\int\limits_2^5 {f\left( x \right)dx} \) bằng
8.
15.
−8.
−15.
Tích phân \(\int\limits_2^3 {{{\left( {2x - 1} \right)}^4}dx} \)có giá trị bằng
1.
2.
\(\frac{{282}}{3}\).
\(\frac{{2882}}{{10}}\).
Giá trị tích phân \(I = \int\limits_0^1 {\frac{{2x + 9}}{{x + 3}}dx} \) là \(a + b\ln 2 + c\ln 3\left( {a,b,c \in \mathbb{Z}} \right)\). Tính giá trị biểu thức \(a - b + c\).
1.
0.
−7.
2.
Cho biết \(\int\limits_0^{\frac{\pi }{2}} {\left( {4 - \sin x} \right)dx} = a\pi + b\) với a, b là các số nguyên. Giá trị của biểu thức \(a + b\) bằng.
1.
−4.
6.
3.
Biết \(\int\limits_0^{\frac{\pi }{2}} {\sin 5x\sin 2xdx} = \frac{a}{b}\) với \(a,b \in \mathbb{Z},a < b\). Tính \(\frac{1}{a}a + b\).
20.
19.
23.
18.
Biết \(I = \int\limits_1^2 {{3^x}dx} = \frac{a}{{\ln 3}}\). Giá trị của a bằng
2.
8.
9.
6.
Đặt \(I = \int\limits_0^1 {\left( {{e^{3x}} + 3{x^2}} \right)dx} = \frac{{{e^3} + a}}{b}\) với \(\left( {a,b \in \mathbb{N}} \right)\). Khi đó \(a - 2b\) bằng
−4.
8.
11.
−1.
Đặt \(I = \int\limits_0^1 {\left( {{e^x} + 3{x^2} + m} \right)dx} \) (m là tham số thực). Tìm m để I = e2.
\({e^2} - e\).
e.
e2 + e.
2e.
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Sau khi xuất phát, ô tô di chuyển với tốc độ \(v\left( t \right) = 2,01t - 0,025{t^2}\left( {0 \le t \le 10} \right)\). Trong đó \(v\left( t \right)\) tính theo m/s, thời gian t tính bằng giây, t = 0 là thời điểm xe xuất phát.
a) Quãng đường xe di chuyển được tính theo công thức là \(s\left( t \right) = 2,01 - 0,05t\left( {0 \le t \le 10} \right)\).
b) Quãng đường xe di chuyển được trong 3 giây là 8,82 m.
c) Quãng đường xe di chuyển được trong giây thứ 9 xấp xỉ 15,277 m.
d) Trong khoảng thời gian không quá 10 giây đầu, khi vận tốc đạt giá trị lớn nhất thì gia tốc của xe là 1,51 m/s2.
Một máy bay di chuyển ra đến đường băng và bắt đầu chạy đà để cất cánh. Giả sử vận tốc của máy bay khi chạy đà được cho bởi \(v\left( t \right) = 5 + 3t\) (m/s) với \(t\)là thời gian kể từ khi máy bay bắt đầu chạy đà. Sau 35 giây thì máy bay cất cánh trên đường băng. Gọi \(s\left( t \right)\) là quãng đường máy bay di chuyển được sau \(t\) giây kể từ lúc bắt đầu chạy đà.
a)\(v\left( t \right) = s'\left( t \right)\).
b) \(s\left( t \right) = \frac{3}{2}{t^2} + 5t + 5\).
c) Quãng đường máy bay di chuyển được sau 6 giây kể từ khi bắt đầu chạy đà là 85 mét.
d) Quãng đường máy bay đã di chuyển từ khi bắt đầu chạy đà đến khi rời đường bằng là 2013 m (kết quả làm tròn đến hàng đơn vị).
Cho hai hàm số \(f\left( x \right)\) và \(g\left( x \right)\), biết \(\int\limits_1^5 {f\left( x \right)dx} = 5\) và \(\int\limits_1^5 {g\left( x \right)dx} = 8\).
a) \(\int\limits_1^5 {2f\left( x \right)dx} = 10\).
b) \(\int\limits_1^5 {\left[ {f\left( x \right) - g\left( x \right)} \right]dx = - 3} \).
c) \(\int\limits_1^5 {\left[ {f\left( x \right) + g\left( x \right)} \right]dx = 13} \).
d) \(\int\limits_1^5 {\left[ {3f\left( x \right) + 2g\left( x \right) - {x^2}} \right]dx > - 10} \).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên
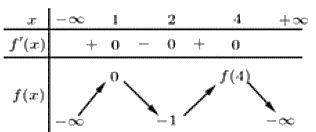
a) \(\int\limits_1^2 {f'\left( x \right)dx} = 1\).
b) \(\int\limits_1^4 {\left[ {3 + f'\left( x \right)} \right]dx} = f\left( 4 \right) + 3\).
c) \(\int\limits_1^2 {\left| {f'\left( x \right)} \right|dx} = f\left( 1 \right) - f\left( 2 \right)\).
d) Nếu \(\int\limits_1^4 {\left| {f'\left( x \right)} \right|dx} = 5\) thì \(f\left( 4 \right) = 3\).
Cho hàm số \(f\left( x \right) = 2{x^2} + 3x + 2\) và hàm số \(g\left( x \right) = x + 1\).
a)\(\int {\left( {x + 1} \right)dx} = \frac{1}{2}{x^2} + x\).
b) \(\int\limits_1^2 {\frac{1}{{g\left( x \right)}}dx} = \ln \frac{3}{2}\).
c) \(\int\limits_1^2 {f\left( x \right)dx} + \int\limits_2^1 {g\left( x \right)dx} = \frac{{26}}{3}\).
d) \(\int\limits_0^2 {\frac{{f\left( x \right)}}{{g\left( x \right)}}dx} = a + b\ln 3\) với \(a,b \in \mathbb{Z}\). Khi đó \(a + b > 8\).
PHẦN III. TRẢ LỜI NGẮN
Cho \(\int\limits_0^1 {f\left( x \right)dx} = 2\). Giá trị của \(\int\limits_0^1 {\left( {2f\left( x \right) + {e^{2x}}} \right)dx} = \frac{{{e^a} + b}}{c}\). Khi đó \(a + b + c\) bằng bao nhiêu?
Cho các hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) liên tục trên \(\mathbb{R}\). Giả sử \(\int\limits_2^7 {\left[ {2f\left( x \right) + 3g\left( x \right)} \right]dx} = 2\) và \(\int\limits_2^7 {\left[ {f\left( x \right) - 2g\left( x \right)} \right]dx} = 4\). Khi đó \(\int\limits_2^7 {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} \) bằng bao nhiêu? (làm tròn kết quả đến chữ số thập phân thứ 2).
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}3{x^2} - x + 1\;\;khi\;x \ge 2\\x - 1\;\;\;\;\;\;\;\;\;\;khi\;x < 2\end{array} \right.\). Tích phân \(I = \int\limits_0^3 {f\left( x \right)dx} \).
Một chiếc máy bay chuyển động trên đường băng với vận tốc \(v\left( t \right) = {t^2} + 10t\) (m/s) với \(t\) là thời gian được tính bằng đơn vị giây kể từ khi máy bay bắt đầu chuyển động. Biết khi máy bay đạt vận tốc 200 m/s thì nó rời đường băng. Quãng đường máy bay đã di chuyển trên đường băng là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị).
Một ô tô xuất phát với vận tốc \({v_1}\left( t \right) = 2t + 12\) (m/s), sau khi đi được khoảng thời gian \({t_1}\) thì bất ngờ gặp chướng ngại vật nên tài xế phanh gấp với vận tốc \({v_2}\left( t \right) = 24 - 6t\)(m/s) và đi thêm một khoảng thời gian \({t_2}\) nữa thì dừng lại. Hỏi từ khi xuất phát đến lúc dừng lại thì xe ô tô đã đi được bao nhiêu mét?








