77 bài tập Một số bài toán thực tế về dạng chuyển động (có lời giải) - Đề 2

 Một ô tô đang chạy với vận tốc \(12\,{\rm{m/s}}\)thì người lái đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc \(v\left( t \right) =  - 3t + 12\left( {{\rm{m/s}}} \right)\), trong đó \(t\)là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét?

Một ô tô đang chạy đều với vận tốc \[15{\rm{ }}m/s\]thì phía trước xuất hiện chướng ngại vật nên người lái đạp phanh gấp. Kể từ thời điểm đó, ô tô chuyển động chậm dần đều với gia tốc \[ - a{\rm{ m/}}{{\rm{s}}^2}.\]Biết ô tô chuyển động thêm được \[20m\]thì dừng hẳn. Tính giá trị của \[a\] (làm tròn đến hàng phần nghìn)?

Một người lái xe ô tô đang chạy với vận tốc \(24\,(m/s)\) thì người lá xe phát hiện vật cản đường ở phía trước nên người lái xe đạp phanh. Từ thời điểm đó, xe chuyển động chậm dần đều với vận tốc \(v(t) =  - 6t + 24{\rm{ }}(m/s)\), trong đó t là khoảng thời gian tính bằng giây, kể từ lúc đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, xe ô tô di chuyển được bao nhiêu mét ?

Một vật chuyển động với vận tốc \(v\left( t \right) = 100 - 10t\,\,\left( {m/s} \right)\,\,\). Quãng đường vật di chuyển từ thời điểm \(t = 0\) đến lúc vật dừng hẳn là?

Một ô tô đang chạy với vận tốc \(15{\rm{ }}\left( {{\rm{m/s}}} \right)\)thì tăng tốc chuyển động nhanh dần với gia tốc \(a = 3t - 8{\rm{ }}\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\), trong đó \(t\)là khoảng thời gian tính bằng giây kể từ lúc tăng vận tốc. Hỏi sau \(10\)giây tăng vận tốc, ô tô đi được bao nhiêu mét ?

Một ô tô đang chạy với tốc độ \(36\,\left( {{\rm{km/h}}} \right)\) thì người lái xe đạp phanh, từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc \(v\left( t \right) =  - 5t + 10\,\left( {{\rm{m/s}}} \right)\), trong đó \(t\) là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến lúc dừng hẳn, ô tô còn di chuyển bao nhiêu mét?

Một ô tô đang chạy với vận tốc không đổi là 20 m/s thì người lái xe đạp phanh. Sau khi đạp phanh, ô tô chuyển động chậm dần đều với vận tốc \(v(t) =  - 4t + 20\) \(\left( {{\rm{m/s}}} \right)\), trong đó \(t\) là khoảng thời gian tính bằng giây. Quãng đường ô tô di chuyển được trong \(10\) giây cuối cùng là

   Một tay đua đang điều khiển chiếc xe đua của mình với vận tốc \[180{\rm{ km/h}}\]. Tay đua nhấn ga để về đích kể từ đó xe chạy với gia tốc \[a\left( t \right) = 2t + 1{\rm{ }}\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\]. Hỏi rằng \[4s\] sau khi tay đua nhấn ga thì xe đua chạy với vận tốc bao nhiêu \[{\rm{km/h}}\]

Một ô tô đang chạy với tốc độ \[20\left( {m/s} \right)\] thì người lái đạp phanh, từ thời điểm đó ô tô chuyển động chậm dần đều với vận tốc \[v\left( t \right) =  - 5t + 20\left( {m/s} \right)\], trong đó \[t\] là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét (\[m\])?

Một vật chuyển động với vận tốc \(10\;m/s\) thì tăng tốc với gia tốc \(a\left( t \right) = 2t + \frac{1}{3}{t^2}\left( {m/{s^2}} \right)\), trong đó \(t\) là khoảng thời gian tính bằng giây kể từ lúc bắt đầu tăng tốc. Hỏi quãng đường vật đi được trong 12 giây kể từ lúc bắt đầu tăng tốc bằng bao nhiêu mét?

Một xe ô tô đang chạy với vận tốc \(20\,\,{\rm{m/s}}\) thì người lái xe nhìn thấy một chướng ngại vật nên đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc \(v\left( t \right) =  - 2t + 20,\) trong đó \(t\) là thời gian (tính bằng giây) kể từ lúc đạp phanh. Quảng đường mà ô tô đi được trong 15 giây cuối cùng bằng

Một ô tô đang chạy với vận tốc là 12 \[\left( {m/s} \right)\]thì người lái đạp phanh; từ thời điểm đó ô tô chuyển động chậm dần đều với vận tốc \(v\left( t \right) =  - 6t + 12\)\[\left( {m/s} \right)\], trong đó \(t\)là khoảng thời gian tính bằng giây kể từ lúc đạp phanh. Hỏi từ lúc đạp phanh đến lúc ô tô dừng hẳn, ô tô còn di chuyển được bao nhiêu mét?

Một vận động viên đua xe \[{\rm{F}}\]đang chạy với vận tốc\[{\rm{10}}\,\left( {{\rm{m/s}}} \right)\]thì anh ta tăng tốc với gia tốc\[a\left( t \right) = 6t\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\], trong đó\[t\]là khoảng thời gian tính bằng giây kể từ lúc tăng tốc. Hỏi quãng đường xe của anh ta đi được trong thời gian\[10\left( {\rm{s}} \right)\]kể từ lúc bắt đầu tăng tốc là bao nhiêu

Một ô tô đang chạy với vận tốc \(15\,\left( {{\rm{m/s}}} \right)\) thì người lái hãm phanh. Sau khi hãm phanh, ô tô chuyển động chậm dần đều với vận tốc \(v\left( t \right) =  - 5t + 15\,\left( {{\rm{m/s}}} \right)\) trong đó \(t\) là khoảng thời gian tính bằng giây kể từ lúc bắt đầu hãm phanh. Hỏi từ lúc hãm phanh đến khi dừng hẳn, ô tô còn di chuyển được bao nhiêu mét ?

Một vật chuyển động với gia tốc \[a(t) = 3{t^2} + t{\rm{ }}({\rm{m/}}{{\rm{s}}^2}).\] Vận tốc ban đầu của vật là \[2\,({\rm{m/s}}).\] Hỏi vận tốc của vật là bao nhiêu sau khi chuyển động với gia tốc đó được \[2\,{\rm{s}}.\]

Một vật chuyển động chậm dần đều với vận tốc \(v(t) = 160 - 10t{\rm{(m/s)}}\). Quãng đường mà vật chuyển động từ thời điểm \(t = 0\left( {\rm{s}} \right)\) đến thời điểm mà vật dừng lại là

Một chất điểm chuyển động thẳng trên trục\(Ox\),với vận tốc cho bởi công thức:\(v(t) = 3{t^2} + 4t\)\((m/s)\). Biết rằng tại thời điểm bắt đầu chuyển động,chất điểm đang ở vị trí có tọa độ \(x = 2\).Tọa độ của chất điểm sau \(1\) giây chuyển động là?

Cho một vật thể bắt đầu chuyển động thẳng với biểu thức vận tốc \(v = \frac{1}{4}{t^2} + k\,\,\left( {{\rm{m/s}}} \right)\). Trong \(10\) giây đầu tiên đi được quãng đường là \(120\,{\rm{m}}\). Hỏi trong \(12\) giây đầu tiên quãng đường vật đi được bằng bao nhiêu?

Cho một vật bắt đầu chuyển động thẳng có vận tốc trong 5 giây đầu tiên là \({t^2}\,\left( {m/s} \right)\) và sau đó giữ cho chuyển động thẳng đều. Quãng đường mà vật đi được trong 20 giây tính từ thời điểm bắt đầu chuyển động bằng:

Một vật đang chuyển động thẳng với vận tốc \({v_0} = 20{\rm{ m/s}}\) thì ở thời điểm \({t_1}\) chịu tác dụng của một lực hãm và gia tốc \(a = 1 - 2t{\rm{ }}\left( {{\rm{m/}}{{\rm{s}}^2}} \right)\). Quãng đường vật đi được tính từ \({t_1}\) đến khi vật dừng lại là

Một chất điểm A xuất phát từ 0, chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật $v\left(t\right)=\frac{1}{180}{t}^2+\frac{11}{18}t(m/s)$, trong đó t (giây) là khoảng thời gian tính từ lúc A bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O, chuyển động thẳng cùng hướng với A nhưng chậm hơn 5 giây so với A và có gia tốc bằng a(m/s) (a là hằng số). Sau khi \[B\] xuất phát được \[10\] giây thì đuổi kịp \[A\]. Vận tốc của \[B\] tại thời điểm đuổi kịp \[A\] bằng

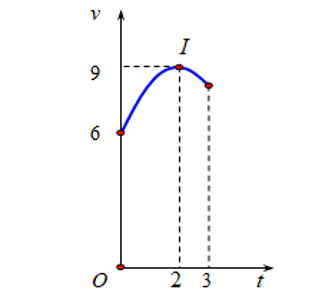
Một vật chuyển động trong \[3\] giờ với vận tốc \[v\left( {{\rm{km/h}}} \right)\] phụ thuộc thời gian \[t\left( {\rm{h}} \right)\]có đồ thị là một phần của đường parabol có đỉnh \[I\left( {2;9} \right)\] và trục đối xứng song song với trục tung như hình bên. Tính quãng đường \[s\]mà vật di chuyển được trong \[3\] giờ đó.

Một vật đang chuyển động với vận tốc \(10\left( {{\rm{m/s}}} \right)\) thì tăng tốc với gia tốc \(a\left( t \right) = 3{t^2} + 2t\,\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\). Tính quãng đường \[S\left( {\rm{m}} \right)\] mà vật đi được trong khoảng thời gian \[12\] giây kể từ lúc bắt đầu tăng tốc.

Một vật chuyển động chậm dần đều với vận tốc \[v\left( t \right) = 150 - 10t{\rm{ }}\left( {{\rm{m/s}}} \right)\] trong đó \(t\) là thời gian tính bằng giây kể từ lúc vật bắt đầu chuyển động chậm dần đều. Trong 4 giây trước khi dừng hẳn, vật di chuyển được quãng đường bằng