23 bài tập Một số bài toán thực tế liên quan đến tích phân (có lời giải)

Một ô tô đang di chuyển với tốc độ 20m/s thì hãm phanh nên tốc độ (m/s) của xe thay đổi theo thời gian t (giây) được tính theo công thức: \[v(t) = 20 - 5t,{\rm{ }}(0 \le t \le 4).\]

a) Kể từ lúc hãm phanh đến khi dừng, ô tô đi được quãng đường bao nhiêu?

b) Tính tốc độ trung bình của xe trong khoảng thời gian đó.

Tại một nhà máy, gọi C(x) là tổng chi phí (tỉnh theo triệu đồng) để sản xuất x tấn sản phẩm A trong một tháng. Khi đó, đạo hàm C'(x), gọi là chi phi cận biên, cho biết tốc độ gia tăng tổng chi phí theo lượng gia tăng sản phẩm được sản xuất. Giả sử chi phí cận biên (tính theo triệu đồng trên tấn) của nhà máy được ước lượng bởi công thức: \[C'(x) = 5 - 0,06x + 0,00072{x^2}\] với \[0 \le x \le 150\]. Biết rằng C(0) = 30 triệu đồng, gọi là chi phí cố định. Tính tổng chi phí khi nhà máy sản xuất 100 tấn sản phẩm A trong tháng.

Sau khi xuất phát, ô tô di chuyển với tốc độ \[v\left( t \right) = 2t - 0,03{t^2},\left( {0{\rm{ }} \le t < 10} \right)\], trong đó v(t) tinh theo m/s, thời gian t tính theo giây với t = 0 là thời điểm xe xuất phát.

a) Tính quãng đường xe đi được sau 5 giây, sau 10 giây.

b) Tính tốc độ trung bình của xe trong khoảng thời gian từ t = 0 đến t =10.

Một ô tô đang chạy với vận tốc 20 m/s thì người lái đạp phanh. Sau khi đạp phanh, ô tô chuyển động chậm dần đều với vận tốc \[v\left( t \right) = 40t{\rm{ }} + 20\] (m/s), trong đó t là thời gian tính bằng giây kể từ lúc đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét?

Một vật chuyển động thẳng trong 10 giây với vận tốc \[v\left( t \right) = 3t + 2\] (m/s). Gọi s(t) là quãng đường vật đi được đến thời điểm t giây (0 < t < 10). Xét chuyển động của vật từ thời điểm t = 3 giây đến thời điểm t = 5 giây. Tính quãng đường đi được của vật trong khoảng thời gian từ 3 giây đến 5 giây.

Một xe ô tô đang chạy với vận tốc \(20\)m/s thì người lái xe nhìn thấy chướng ngại vật nên đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc là \(v\left( t \right) =  - 2t + 20\), trong đó \(t\) là thời gian (tính bằng giây) kể từ lúc đạp phanh. Quãng đường mà ô tô đi được trong \(15\) giây cuối cùng là bao nhiêu.

Một vật chuyển động với tốc độ \[v\left( t \right) = 3t + 4\] (m/s), với thời gian t tinh theo giây, t = [0; 5]. Tính quãng đường vật đi được trong khoảng thời gian từ t = 0 đến t = 5.

Một chất điểm đang chuyển động với tốc độ v = 1 m/s thì tăng tốc với gia tốc không đổi a = 3 m/s2. Hỏi tốc độ của chất điểm là bao nhiêu sau 10 giây kể từ khi bắt đầu tăng tốc?

Sau khi được thả rơi tự do từ độ cao 100 m, một vật rơi xuống với tốc độ v(t)=10t (m/s), trong đó t là thời gian tính theo giây kể từ khi thả vật.

a) Tính quãng đường s(t) vật di chuyển được sau thời gian t giây (trong khoảng thời gian vật đang rơi).

b) Sau bao nhiêu giây thì vật chạm đất? Tính tốc độ rơi trung bình của vật.

Một ô tô đang chạy với vận tốc 20 (m/s) thì người lái đạp phanh, từ thời điểm đó ô tô chuyển động với vận tốc v(t) = −5t + 20 (m/s), trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu đạp phanh.

a) Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển thêm một quãng đường dài bao nhiêu mét?

b) Tính tốc độ trung bình của xe trong khoảng thời gian đó.

Giá trị trung bình của hàm số liên tục f(x) trên đoạn [a; b] được định nghĩa là \[\frac{1}{{b - a}}\int\limits_a^b {f(x)dx} \]. Giả sử nhiệt độ (tính bằng °C) tại thời điểm t giờ trong khoảng thời gian từ 6 giờ sáng đến 12 giờ trưa ở một địa phương vào một ngày nào đó được mô hình hoá bởi hàm số \[T\left( t \right) = 20 + 1,5\left( {t - 6} \right),{\rm{ }}6 \le t \le 12\].Tìm nhiệt độ trung bình vào ngày đó trong khoảng thời gian từ 6 giờ sáng đến 12 giờ trưa.

a) Cho một vật chuyển động với vận tốc \(y = v(t)\) \(({\rm{m}}/{\rm{s}})\). Cho \(0 < {\rm{a}} < {\rm{b}}\) và \({\rm{v}}({\rm{t}}) > 0\) với mọi \({\rm{t}} \in [{\rm{a}};{\rm{b}}]\). Hãy giải thích vì sao \(\int_a^b v (t)dt\) biểu thị quãng đường mà vật đi được trong khoảng thời gian từ a đến \({\rm{b}}({\rm{a}},{\rm{b}}\) tính theo giây).

b) Áp dụng công thức ở câu a) để giải bài toán sau: Một vật chuyển động với vận tốc \(v(t) = 2 - \sin t(\;{\rm{m}}/{\rm{s}})\). Tính quãng đường vật di chuyển trong khoảng thời gian từ thời điểm \(t = 0\) (giây) đến thời điểm \(t = \frac{{3\pi }}{4}\) (giây).

Một vật chuyển động dọc theo một đường thẳng sao cho vận tốc của nó tại thời điểm t (giây) là \[v(t) = {t^2} - t - 6\] (m/s).

a) Tìm độ dịch chuyển của vật trong khoảng thời gian \[1 \le t \le 4\], tức là tính \[\int\limits_1^4 {v(t)dt} \].

b) Tìm tổng quãng đường vật đi được trong khoảng thời gian này, tức là tính \[\int\limits_1^4 {\left| {v(t)} \right|dt} \].

Giả sử lợi nhuận biên (tính bằng triệu đồng) của một sản phẩm được mô hình hoá bằng công thức: \[P'\left( x \right) =  - 0,0005x + 12,2\]. Ở đây P(x) là lợi nhuận (tính bằng triệu đồng) khi bán được x đơn vị sản phẩm.

a) Tìm sự thay đổi của lợi nhuận khi doanh số tăng từ 100 lên 101 đơn vị sản phẩm.

b) Tìm sự thay đổi của lợi nhuận khi doanh số tăng từ 100 lên 110 đơn vị sản phẩm.

Tại một nhà máy sản xuất một loại phân bón, gọi P(x) là lợi nhuận (tính theo triệu đồng) thu được từ việc bán x tấn sản phẩm trong một tuần. Khi đó, đạo hàm P'(x), gọi là lợi nhuận cận biên, cho biết tốc độ tăng lợi nhuận theo lượng sản phẩm bán được. Giả sử lợi nhuận cận biên (tinh theo triệu đồng trên tấn) của nhà máy được ước lượng bởi công thức: P'(x)= 16 – 0,02x với 0 ≤ x ≤ 100. Tính lợi nhuận nhà máy thu được khi bán 90 tấn sản phẩm trong tuần. Biết rằng nhà máy lỗ 25 triệu đồng nếu không bán được lượng sản phẩm nào trong tuần.

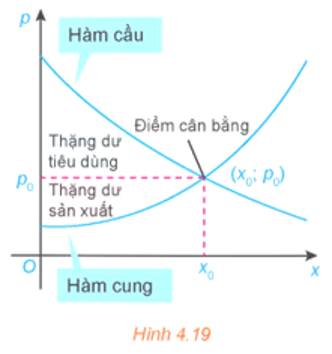
Ta biết rằng hàm cầu liên quan đến giá p của một sản phẩm với nhu cầu của người tiêu dùng, hàm cung liên quan đến giá p của sản phẩm với mức độ sẵn sàng cung cấp sản phẩm của nhà sản xuất. Điểm cắt nhau \(\left( {{{\rm{x}}_0};{{\rm{P}}_0}} \right)\) của đồ thị hàm cầu \({\rm{p}} = {\rm{D}}({\rm{x}})\) và đồ thị hàm cung p \( = {\rm{S}}({\rm{x}})\) được gọi là điểm cân bằng.

Các nhà kinh tế gọi diện tích của hình giới hạn bởi đồ thị hàm cầu, đường ngang \({\rm{p}} = {{\rm{p}}_0}\) và đường thẳng đứng \({\rm{x}} = 0\) là thặng dư tiêu dùng. Tương tự, diện tích của hình giới hạn bởi đồ thị của hàm cung, đường nằm ngang \({\rm{p}} = {{\rm{p}}_0}\) và đường thẳng đứng \(x = 0\) được gọi là thặng dư sản xuất, như trong Hình 4.19.

(Theo R.Larson, Brief Calculus: An Applied Approach, \({8^{{\rm{th }}}}\) edition, Cengage Learning, 2009).

Giả sử hàm cung và hàm cầu của một loại sản phẩm được mô hình hóa bởi:

Hàm cầu: \(p =  - 0,36x + 9\) và hàm cung: \(p = 0,14x + 2\), trong đó \(x\) là số đơn vị sản phẩm. Tìm thặng dư tiêu dùng và thặng dư sản xuất cho sản phẩm này.

Biết rằng tốc độ v (km/phút) của một ca nô cao tốc thay đổi theo thời gian t (phút) như sau:\[v(t) = \left\{ \begin{array}{l}0,5t{\rm{        }},0 \le t < 2\\1{\rm{            }},2 \le t < 15\\4 - 0,2t{\rm{    }},15 \le t \le 20\end{array} \right.\]. Tính quãng đường ca nô di chuyển được trong khoảng thời gian t từ 0 đến 20 phút.

Mặt cắt ngang của một ống dẫn khí nóng là hình vành khuyên như Hình vẽ. Khí bên trong ống được duy trì ở 150 $°C$. Biết rằng nhiệt độ $T(°C)$ tại điềm \({\rm{A}}\) trên thành ống là hàm số của khoảng cách \(x(\;{\rm{cm}})\) từ \({\rm{A}}\) đến tâm của mặt cắt và \({T^\prime }(x) =  - \frac{{30}}{x}\quad (6 \le x \le 8).\)

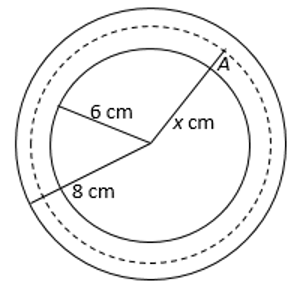
(Nguồn: Y.A.Çengel, A.I.Gahjar, Heat and Mass Transfer, Mc Graw Hill, 2015)

Tìm nhiệt độ mặt ngoài của ống.

Tốc độ v (m/s) của một thang máy di chuyển từ tầng 1 lên tầng cao nhất theo thời gian t (giây) được cho bởi công thức: \[v(t) = \left\{ \begin{array}{l}t{\rm{             }},0 \le t \le 2\\2{\rm{             }},2 < t \le 20\\12 - 0,5t{\rm{    }},20 < t \le 24\end{array} \right.\]. Tính quãng đường chuyển động và tốc độ trung bình của thang máy.

Giả sử vận tốc v của dòng máu ở khoảng cách r từ tâm của động mạch bán kính R không đổi, có thể được mô hình hoá bởi công thức: \[v = k\left( {{R^2} - {r^2}} \right),\]trong đó k là một hằng số. Tìm vận tốc trung bình (đối với r) của động mạch trong khoảng \[0 \le r \le R\]. So sánh vận tốc trung bình với vận tốc lớn nhất.

Một vật chuyển động được cho bởi đồ thị như hình bên.

a) Tính quãng đường mà vật di chuyển được trong 1 giây đầu tiên.

b) Tính quãng đường mà vật di chuyển được trong 2 giây đầu tiên.

Ở nhiệt độ 370C, một phản ứng hóa học từ chất A, chuển hóa thành sản phầm B theo phương trình phản ứng \[A \to B\]. Giả sử y(x) là nồng độ chất A ( đơn vị mol L-1) tại thời gian x (giây), y(x) > 0 với \[x \ge 0\], thỏa mãn hệ thức \[y'(x) =  - {7.10^{ - 4}}y(x)\] với mọi \[x \ge 0\]. Biết rằng tại x = 0, nồng độ (đầu) của A là 0,05 mol L-1.

a) Xét hàm số f(x) = lny(x) với \[x \ge 0\]. Hãy tính f’(x), từ đó hãy tìm hàm số f(x).

b) Giả sử ta tính nồng độ trung bình chất A (đơn vị mol L-1) từ thời điểm a (giây) đến thời điểm b (giây) với \[0 < a < b\] theo công thức \[\frac{1}{{b - a}}\int\limits_a^b {f(x)dx} \]. Xác định nồng độ trung bình của chất A từ thời điểm 15 giây đến thời điểm 30 giây.