(Trả lời ngắn) 22 bài tập Ứng dụng hình học của tích phân (có lời giải)

Kí hiệu \[S\left( t \right)\] là diện tích của hình phẳng giới hạn bởi các đường \[y = 2x + 1\], \[y = 0\], \[x = 1\], \[x = t\]\[\left( {t > 1} \right)\]. Tìm \[t\] để \[S\left( t \right) = 10\].

Trả lời: ………………..

Giá trị dương của tham số \(m\) sao cho diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = 2x + 3\) và các đường thẳng \(y = 0,\,x = 0\,,\,x = m\) bằng \(10\) là bao nhiêu?

Trả lời: ………………..

Hình vuông \(OABC\) có cạnh bằng \(4\) được chia thành hai phần bởi đường cong \(\left( C \right)\) có phương trình \(y = \frac{1}{4}\,{x^2}\). Gọi \({S_1}\,,\,\,{S_2}\) lần lượt là diện tích của phần không bị gạch và bị gạch như hình vẽ bên dưới. Tỉ số \(\frac{{{S_1}}}{{{S_2}}}\) bằng bao nhiêu?

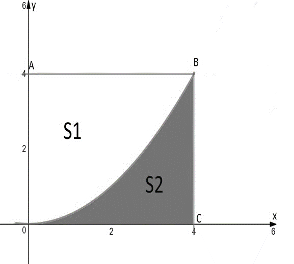
Trả lời: ………………..

Cho hình thang cong \[\left( H \right)\] giới hạn bởi các đường \[y = {{\rm{e}}^x}\], \[y = 0\], \[x = 0\], \[x = \ln 4\]. Đường thẳng \[x = k\] \[\left( {0 < k < \ln 4} \right)\] chia \[\left( H \right)\] thành hai phần có diện tích là \[{S_1}\] và \[{S_2}\] như hình vẽ bên. Tìm \[k\] để \[{S_1} = 2{S_2}\].

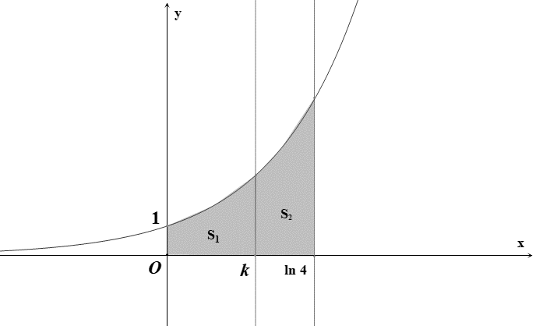
Trả lời: ………………..

Cắt một vật thể \(\left( T \right)\) bởi hai mặt phẳng vuông góc với trục \[Ox\] tại \(x = 0\) và \(x = 2\). Một mặt phẳng tùy ý vuông góc với trục \[Ox\] tại điểm có hoành độ \(x\left( {0 \le x \le 2} \right)\) cắt vật thể đó có diện tích diện là một hình vuông có cạnh bằng \(\sqrt {{x^3}} \). Tính thể tích vật thể \(\left( T \right)\).

Trả lời: ………………..

Cắt một vật thể  bởi hai mặt phẳng vuông góc với trục \[Ox\] tại \(x = 1\,;\,x = 3\). Khi cắt một vật thể bởi mặt phẳng vuông góc với trục \[Ox\] tại điểm có hoành độ \(x\) (\(1 \le x \le 3\)), mặt cắt là tam giác vuông có một góc \({45^0}\) và độ dài một cạnh góc vuông là \(\sqrt {4 - \frac{1}{2}{x^2}} \). Tính thể tích vật thể trên.

Trả lời: ………………..

Tính thể tích khối tròn xoay khi quay hình phẳng \(\left( H \right)\) xác định bởi các đường \(y = \frac{1}{3}{x^3} - {x^2}\), \(y = 0\), \(x = 0\) và \(x = 3\) quanh trục \[Ox\].

Trả lời: ………………..

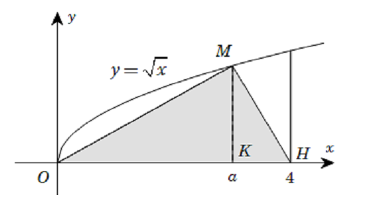
Gọi \(V\) là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi

các đường \(y = \sqrt x \), \(y = 0\) và \(x = 4\) quanh trục \(Ox\). Đường thẳng \(x

= a\;\left( {0 < a < 4} \right)\) cắt đồ thị hàm số \(y = \sqrt x \) tại \(M\) (hình vẽ).

Gọi \({V_1}\) là thể tích khối tròn xoay tạo thành khi quay tam giác \(OMH\)

quanh trục \(Ox\). Biết rằng \(V = 2{V_1}\). Khi đó

Trả lời: ………………..

Khi cắt một vật thể hình chiếc niêm bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x \[\left( { - 2 \le x \le 2} \right)\], mặt cắt là tam giác vuông có một góc ${45}^o$ và độ dài một cạnh góc vuông là \[\sqrt {4 - {x^2}} \] (dm) như hình vẽ. Tính thể tích của vật thể.

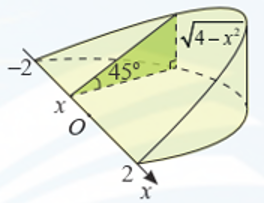
Trả lời: ………………..

Cho D là hình phẳng giới hạn bởi đồ thị hàm số \[y = \sqrt {4 - x} \] \[\left( {x \le 4} \right)\], trục tung và trục hoành như hình vẽ. Tính thể tích khối tròn xoay tạo thành khi xoay D quanh trục Ox.

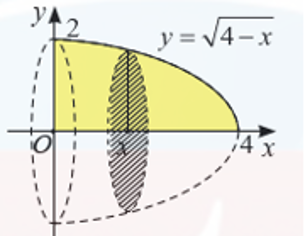
Trả lời: ………………..

 Trong mặt phẳng tọa độ Oxy, cho hình thang OABC có A(0; 1), B(2; 2), C(2; 0) như hình vẽ. Tính thể tích khối tròn xoay tạo thành khi quay hình thang OABC quanh trục hoành.

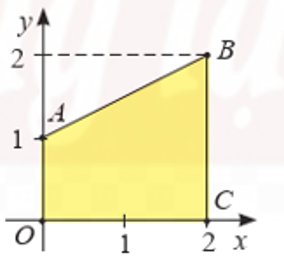
Trả lời: ………………..

Một vật chuyển động với tốc độ \(v(t) = 3t + 4\) \(({\rm{m}}/{\rm{s}})\), với thời gian t tính theo giây, \({\rm{t}} \in [0;5]\). Tính quãng đường vật đi được trong khoảng thời gian từ \({\rm{t}} = 0\) đến \({\rm{t}} = 5\).

Trả lời: ………………..

Một chất điểm đang chuyển động với tốc độ vo \( = 1\;{\rm{m}}/{\rm{s}}\) thì tăng tốc với gia tốc không đổi \({\rm{a}} = 3\;{\rm{m}}/{{\rm{s}}^2}\). Hỏi tốc độ của chất điểm là bao nhiêu sau 10 giây kể từ khi bắt đầu tăng tốc.

Trả lời: ………………..

Hình minh họa mặt cắt của một bức thường cũ có dạng hình chữ nhật với một cổng ra và có dạng hình parabol với các kích thước được cho hinh hình bên. Người ta dự định sơn lại mặt ngoài của béc tường đó. Chi phí để sơn bức tường là 15000 đồng/1m2 . Tổng chi phí để sơn toàn bộ mặt ngoài của bức tường là bao nhiêu

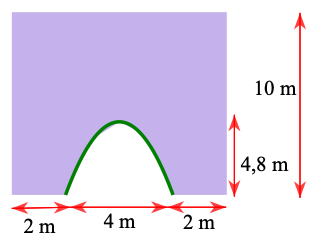
Trả lời: ………………..

Người ta  dự định lắp kính cho cửa một mái vòm có dạng hình parabol. Hãy tính diện tích mặt kính cần lắp vào, biết rằng mái vòm cao 21 m và rộng 70 m

Trả lời: ………………..

Cửa vòm lấy ánh sáng của một tòa nhà được thiết kế dạng parabol với kích thước như hình vẽ. Người ta định lắp kính cho cửa này. Tính diện tích kính cần lắp, biết rằng người ta chỉ sử dụng một lớp kính và bỏ qua diện tích của khung cửa.

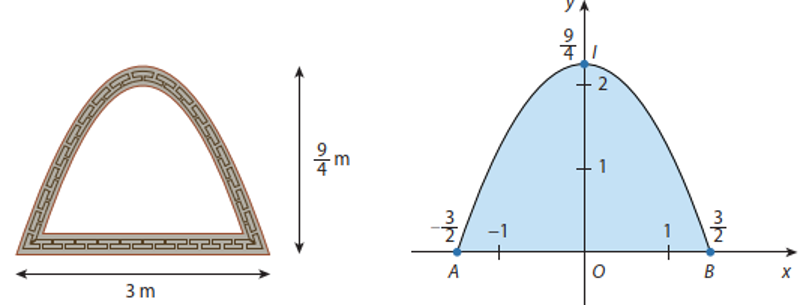
Trả lời: ………………..

Một bình chứa nước có hình dạng như Hình 11. Biết rằng khi nước trong bình có chiều cao \(x({\rm{dm}})(0 \le x \le 4)\) thì mặt nước là hình vuông có cạnh \(\sqrt {2 + \frac{{{x^2}}}{4}} ({\rm{dm}})\). Tính dung tích của bình.

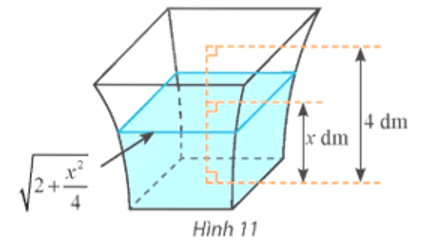
Trả lời: ………………..

Hình vẽ mô phỏng phần bên trong của một chậu cây có dạng khối tròn xoay tạo thành khi quay một phần của đồ thị hàm số \[y = \sqrt x  + \frac{3}{2}\] với \[0 \le x \le 4\] quanh trục hoành. Thể tích phần bên trong (dung tích) của chậu cây, biết đơn vị trên các trục Ox, Oy là decimet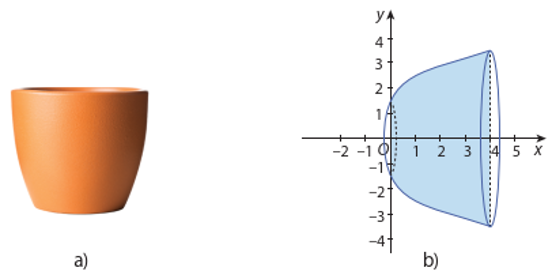

Trả lời: ………………..

Sau khi đo kích thức hai thùng rượu vang như hình bên, bạn Quân xác định thù rượu vang có dạng hình tròn xoay được tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số \[y =  - 0,011{x^2} - 0,071x + 40\], trục Ox và hai đường thẳng x = -35, x = 35 quay quanh trục Ox. Tính thể tích thùng rượu vang đó biết đơn vị trên mỗi trục tọa độ là centimet.

Trả lời: ………………..

Nếu cắt chậu nước có hình dạng như Hình vẽ bằng mặt phẳng song song và cách mặt đáy x (cm) (0 ≤ x ≤ 16) thì mặt cắt là hình tròn có bán kính \[\left( {10 + \sqrt x } \right)\] (cm). Tính dung tích của chậu.

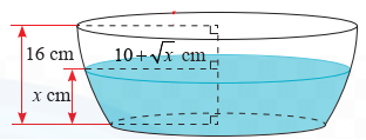
Trả lời: ………………..

Một chiếc lều mái vòm có hình dạng như Hình vẽ. Nếu cắt lều bằng mặt phẳng song song với mặt đáy và cách mặt đáy một khoảng x (m) (0 ≤ x ≤ 3) thì được hình vuông có cạnh \[\sqrt {9 - {x^2}} \] (m). Tính thể tích của lều.

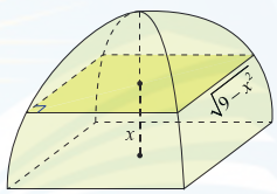
Trả lời: ………………..