13 bài tập Thể tích khối tròn xoay quanh trục Ox (có lời giải)

Gọi \(\left( H \right)\)là hình phẳng giới hạn bởi đồ thị hàm số \(y = {e^x}\), trục \(Ox\)và hai đường thẳng \(x = 0,\) \(x = 1\). Thể tích của khối tròn xoay tạo thành khi quay \(\left( H \right)\) xung quanh trục\(Ox\) là

Cho hình phẳng \(\left( H \right)\) giới hạn bởi đồ thị hàm số \(y = \frac{1}{x}\) và các đường thẳng \(y = 0\), \(x = 1\), \(x = 4\). Thể tích \(V\) của khối tròn xoay sinh ra khi cho hình phẳng \(\left( H \right)\) quay quanh trục \(Ox\).

   Cho hình phẳng giới hạn bởi đồ thị hàm số \[f(x) = \sin \frac{x}{2}\], trục hoành và hai đường thẳng x = 0, \[x = \frac{\pi }{2}\]. Tính thể tích khối tròn xoay tạo thành khi cho hình phẳng đó quay quanh trục Ox.

Cho hình phẳng \(D\) giới hạn bởi đường cong \(y = \sqrt {2 + \cos x} ,\) trục hoành và các đường thẳng \(x = 0,x = \frac{\pi }{2}\). Khối tròn xoay tạo thành khi \(D\) quay quanh trục hoành có thể tích \(V\) bằng bao nhiêu?

Kí hiệu \[\left( H \right)\] là hình phẳng giới hạn bởi đồ thị hàm số \[y = 2x--{x^2}\] và \[y = 0\]. Tính thể tích vật thể tròn xoay được sinh ra bởi hình phẳng \[\left( H \right)\] khi nó quay quanh trục \[Ox\].

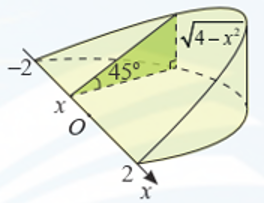
Khi cắt một vật thể hình chiếc niêm bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x \[\left( { - 2 \le x \le 2} \right)\], mặt cắt là tam giác vuông có một góc ${45}^{\circ }$ và độ dài một cạnh góc vuông là \[\sqrt {4 - {x^2}} \] (dm) như hình vẽ. Tính thể tích của vật thể.

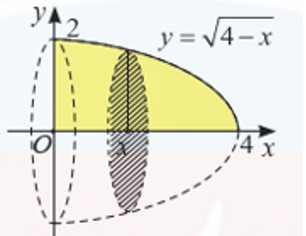
 Cho D là hình phẳng giới hạn bởi đồ thị hàm số \[y = \sqrt {4 - x} \] \[\left( {x \le 4} \right)\], trục tung và trục hoành như hình vẽ. Tính thể tích khối tròn xoay tạo thành khi xoay D quanh trục Ox.

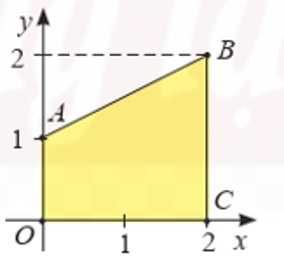
Trong mặt phẳng tọa độ Oxy, cho hình thang OABC có A(0; 1), B(2; 2), C(2; 0) như hình vẽ. Tính thể tích khối tròn xoay tạo thành khi quay hình thang OABC quanh trục hoành.

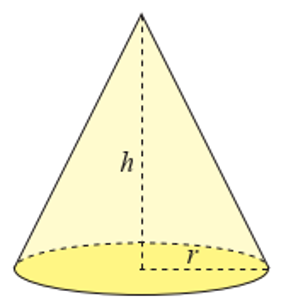
Sử dụng tích phân để tích thể tích của khối nón có bán kính đáy r và chiều cao h như hình vẽ.

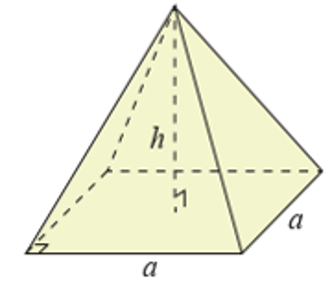
 Sử dụng tích phân để tích thể tích của khối chóp có cạnh đáy a và chiều cao h như hình vẽ.

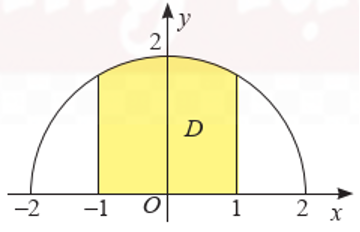
Trên mặt phẳng tọa độ Oxy, vẽ nửa đường tròn tâm O, bán kính r = 2, nằm phía trên trục Ox. Gọi D là hình phẳng giới hạn bởi nửa đường tròn, trục Ox  và hai đường thẳng x = -1, x = 1. Tính thể tích khối tròn xoay tạo thành khi quay D quanh trục Ox.

Cho tam giác OAB có cạnh OA = a nằm trên trục Ox và \[\widehat {AOB} = \alpha {\rm{ }}\left( {0 < \alpha  \le \frac{\pi }{4}} \right)\]. Gọi (B) là khối tròn xoay sinh ra khi quay miền tam giác OAB xung quanh Ox như hình vẽ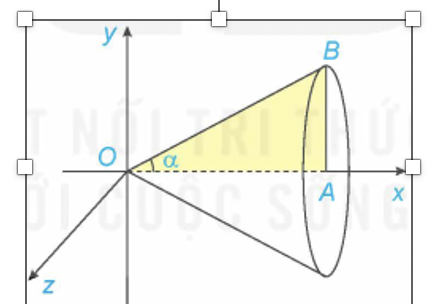

a) Tính thể tích V của (B) theo a và \[\alpha \].

b) Tìm \[\alpha \] sao cho thể tích V lớn nhất.