10 bài tập Tính thể tích vật thể khi biết thiết diện được cắt bởi mặt phẳng vuông góc với trục Ox (có lời giải)

Một vật thể nằm giữa hai mặt phẳng \[x =  - 1\], \[x = 1\] và thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ \[x{\rm{ }}( - 1 \le x \le 1)\] là một hình tròn có diện tích bằng \[3\pi \]. Thể tích của vật thể là

Cho một vật thể \(B\) nằm dọc theo trục \(Ox\), được giới hạn từ \(x = 0\) đến \(x = 2\). Một mặt phẳng vuông góc với trục \[Ox\] tại điểm có hoành độ \(x \in \left[ {0;2} \right]\) cắt vật thể \(B\) theo một thiết diện có diện tích là \(S\left( x \right) = 3{x^2}\). Thể tích vật thể \(B\) bằng:

Tính thể tích \(V\)của vật thể tròn xoay giới hạn bởi hai mặt phẳng \(x = 1\)và \(x = 4\), biết rằng khi cắt bởi mặt phẳng tùy ý vuông góc với \(Ox\)tại điểm có hoành độ \(x\,\,\left( {1 \le x \le 4} \right)\)thì được thiết diện là lục giác đều có độ dài cạnh là \(2x\).

 Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng \(x = 1\) và \(x = 3\), biết rằng khi cắt vật thể bởi mặt phẳng vuông góc với trục \[Ox\] tại điểm có hoành độ \(x\) (\(1 \le x \le 3\)) thì được thiết diện là một hình chữ nhật có độ dài hai cạnh là \(3x\) và \(\sqrt {3{x^2} - 2} \).

Tính thể tích của vật thể nằm giữa hai mặt phẳng \(x =  - 1\) và \(x = 1\) biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục \(Ox\)tại điểm có hoành độ \(x\left( { - 1 \le x \le 1} \right)\) là một hình vuông có cạnh bằng \(\sqrt {1 - {x^4}} \).

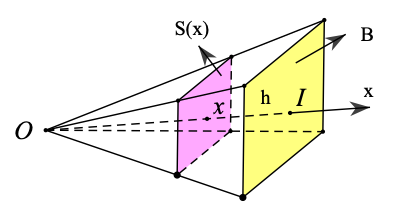
Cho khối chóp có chiều cao bằng h và diện tích bằng B. Chọ trục Ox vuông góc với mặt phẳng đáy tại điểm I sao cho gốc O trùng với đỉnh của khối chóp và có hướng xác định bởi véctơ \[\overrightarrow {OI} \] như hình bên. Khi OI = h. Một mặt phẳng (P) vuông góc với trục Ox tại x \[\left( {0 \le x \le h} \right)\], cắt khối chóp theo hình phẳng có diện tích S(x). Người ta chứng minh rằng \[S(x) = B\frac{{{x^2}}}{{{h^2}}}\]. Tính thể tích khối chóp đó.

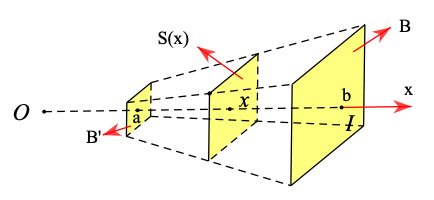
 Cho khối chóp cụt đều tạo bởi khối chóp đỉnh S, diện tích hai đáy lần lượt là B, B’ và chiều cao h. Chọn trục Ox chứa đường cao của khối chóp và gốc O trùng với đỉnh S. Hai mặt phẳng đáy của khối chóp cụt đều lần lượt cắt Ox tại I và I’ . Đặt OI = b, OI’ = a (a< b). Một mặt phẳng (P) vuông góc với trục Ox tại x \[\left( {a \le x \le b} \right)\], cắt khối chóp cụt đều theo hình phẳng có diện tích S(x). Người ta chứng minh rằng \[S(x) = B\frac{{{x^2}}}{{{b^2}}}\]. Tính thể tích khối chóp cụt đó.

Trong không gian, cho hình chóp $O . A B C D$ có đáy là hình vuông cạnh \(a,OA \bot (ABCD),OA = h\). Đặt trục số Ox như Hình 8 . Một mặt phẳng vuông góc với trục Ox tại điểm có hoành độ \({\rm{x}}(0 < {\rm{x}}\) \( \le \) h), cắt hình chóp OABCD theo mặt cắt là hình vuông \({A^\prime }{B^\prime }{C^\prime }{D^\prime }\). Kí hiệu \(S(x)\) là diện tích của hình vuông \({A^\prime }{B^\prime }{C^\prime }{D^\prime }\).

a) Tính \(S(x)\) theo a, h và \(x\).

b) Tính \(\int_0^h S (x)dx\) và so sánh với thể tích của khối chóp O.ABCD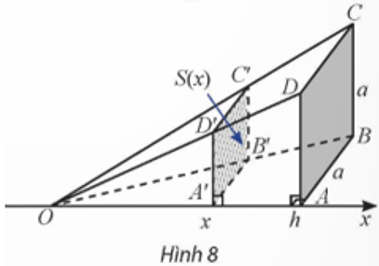

Ta đã biết công thức tính thể tích của khối cầu bán kính R là \(V = \frac{{4\pi {R^3}}}{3}\). Em hãy chứng minh công thức đó.