20 câu trắc nghiệm Toán 12 Chân trời sáng tạo Bài 3. Ứng dụng hình học của tích phân (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = {e^x} - 2\), trục hoành và hai đường thẳng \(x = 0,x = \ln 4\) là
1.
3.
2ln2 – 1.
3 – 4ln2.
Diện tích hình phẳng giới hạn bởi trục Ox, trục Oy, đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(x = 2\) được tính theo công thức nào dưới đây?
\(\int\limits_2^0 {\left| {f\left( x \right)} \right|dx} \).
\(\int\limits_0^2 {\left| {f\left( x \right) - 2} \right|dx} \).
\(\int\limits_0^2 {f\left( x \right)dx} \).
\(\int\limits_0^2 {\left| {f\left( x \right)} \right|dx} \).
Gọi \(S\) là diện tích hình phẳng giới hạn bởi các đường \(y = {3^x},y = 0,x = 0,x = 2\). Mệnh đề nào dưới đây đúng?
\(\int\limits_0^2 {{3^x}dx} \).
\(\pi \int\limits_0^2 {{3^{2x}}dx} \).
\(\pi \int\limits_0^2 {{3^x}dx} \).
\(\int\limits_0^2 {{3^{2x}}dx} \).
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = \cos x\), trục tung, trục hoành và đường thẳng \(x = \pi \) bằng
2.
3.
1.
4.
Tính diện tích S của hình phẳng (phần gạch sọc) trong hình sau
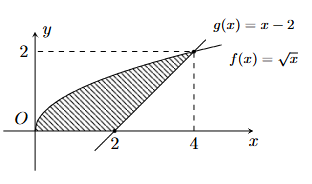
\(S = \frac{{16}}{3}\).
\(S = \frac{{10}}{3}\).
\(S = \frac{{11}}{3}\).
\(S = \frac{7}{3}\).
Cho đồ thị của hàm số \(y = f\left( x \right)\) như hình vẽ
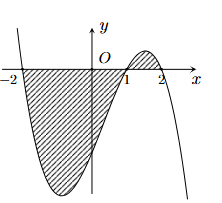
Biết \(\int\limits_{ - 2}^1 {f\left( x \right)dx} = a,\int\limits_1^2 {f\left( x \right)dx} = b\). Tính diện tích S của phần hình phẳng được gạch chéo.
\(S = - a - b\).
\(S = a + b\).
\(S = b - a\).
\(S = a - b\).
Thể tích khối tròn xoay sinh ra khi cho hình phẳng (H) giới hạn bởi các đường \(y = x\sqrt x \); y = 0; x = 0; x = 1 xoay quanh trục Ox là
\(S = \frac{1}{4}\).
\(S = \frac{\pi }{4}\).
\(S = \frac{{2\pi }}{5}\).
\(S = \frac{\pi }{2}\).
Cho hình phẳng (H) giới hạn bởi đồ thị hàm số \(y = - {x^2} + 3x - 2\), trục hoành và hai đường thẳng \(x = 1,x = 2\). Quay (H) quanh trục hoành được khối tròn xoay có thể tích là
\(V = \int\limits_1^2 {\left| {{x^2} - 3x + 2} \right|dx} \).
\(V = \int\limits_1^2 {{{\left| {{x^2} - 3x + 2} \right|}^2}dx} \).
\(V = \pi \int\limits_1^2 {{{\left( {{x^2} - 3x + 2} \right)}^2}dx} \).
\(V = \pi \int\limits_1^2 {\left| {{x^2} - 3x + 2} \right|dx} \).
Cho vật thể được giới hạn bởi hai mặt phẳng \(x = 1,x = 3\). Cắt vật thể đã cho bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ bằng x, \(1 \le x \le 3\) ta được thiết diện có diện tích bằng \(3{x^2} + 2x\). Thể tích của vật thể đã cho là
\(V = 42\pi \).
\(V = 42\).
\(V = 34\).
\(V = 34\pi \).
Cho hình phẳng giới hạn bởi các đường \(y = \sqrt {\tan x} ,y = 0,x = 0,x = \frac{\pi }{4}\) quay xung quanh trục \(Ox\). Tính thể tích vật thể tròn xoay được sinh ra.
\(\frac{{\pi \ln 2}}{2}\).
\(\frac{{\pi \ln 3}}{4}\).
\(V = \frac{\pi }{4}\).
\(V = \pi \ln 2\).
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho hàm số \(f\left( x \right) = {x^2} - 2x\) có đồ thị là (C) và đường thẳng d: y = x.
a) Tích phân \(\int\limits_0^1 {f\left( x \right)dx} = - \frac{2}{3}\).
b) Hình phẳng giới hạn bởi (C), trục hoành và hai đường thẳng x = 1, x = 2 có diện tích bằng \(\frac{4}{3}\).
c) Hình phẳng giới hạn bởi (C) và d có diện tích bằng \(\frac{9}{2}\).
d) Gọi (H) là hình phẳng giới hạn bởi (C), trục hoành và hai đường thẳng \(x = 0,x = 1\). Khối tròn xoay thu được khi cho (H) quay quanh trục hoành có thể tích bằng \(\frac{{8\pi }}{{15}}\).
Cho hàm số \(y = \sqrt {x + 2} \left( {x \ge - 2} \right)\) và đường thẳng \(y = x\).
a) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = \sqrt {x + 2} \) và đường thẳng \(y = x\), hai đường thẳng \(x = 0,x = 2\) là \(S = \frac{{10}}{3} - \frac{{2\sqrt 2 }}{9}\) (đơn vị diện tích).
b) Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đường thẳng y = x, trục hoành, hai đường thẳng x = 1, x = 3 quanh trục Ox là 5π (đơn vị diện tích).
c) Diện tích hình phẳng D giới hạn bởi đồ thị hàm số \(y = \sqrt {x + 2} \left( {x \ge - 2} \right)\), trục tung, trục hoành và đường thẳng x = 2 là \({S_D} = \frac{{16}}{3} - \frac{{4\sqrt 2 }}{3}\) (đơn vị diện tích).
d) Thể tích khối tròn xoay tạo thành khi quay hình phẳng D quanh trục Ox là 6π (đơn vị diện tích).
Cho hình phẳng (H) giới hạn bởi các đường \(y = {x^2} - 4,y = 0,x = - 2,x = 2\).
a) Công thức tính diện tích hình phẳng (H) là \({S_H} = \int\limits_{ - 2}^2 {\left( {{x^2} - 4} \right)dx} \).
b) Diện tích hình phẳng (H) bằng \(\frac{{32}}{3}\).
c) Công thức tính thể tích khối tròn xoay sinh ra khi quay hình phẳng (H) xung quanh trục Ox là \(V = \int\limits_{ - 2}^2 {{{\left( {{x^2} - 4} \right)}^2}dx} \).
d) Thể tích khối tròn xoay sinh ra khi quay hình phẳng (H) xung quanh trục Ox bằng \(\frac{{512}}{{15}}\).
Cho vật thể (T) giới hạn bởi hai mặt phẳng \(x = - 1;x = 1\). Cắt vật thể (T) bởi mặt phẳng vuông góc với trục \(Ox\) tại \(x\left( { - 1 \le x \le 1} \right)\) thu được thiết diện là một hình vuông có cạnh bằng \(2\sqrt {1 - {x^2}} \).
a) Mặt cắt có diện tích \(S\left( x \right)\) liên tục trên \(\left[ { - 1;1} \right]\).
b) Thể tích vật thể được tính theo công thức \(V = \pi \int\limits_{ - 1}^1 {S\left( x \right)dx} \).
c) Diện tích của mặt cắt là \(S\left( x \right) = 2\left( {1 - {x^2}} \right)\).
d) Thể tich của vật thể (T) bằng \(\frac{{16}}{3}\).
Cho đồ thị hàm số \(y = {x^2} - 3x + 2\) và \(y = x - 1\) và \({S_1};{S_2}\) là phần diện tích phần được tô như hình bên dưới
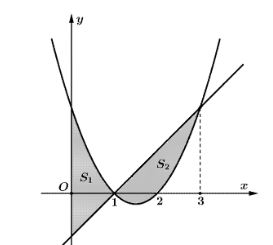
a) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^2} - 3x + 2\) và \(y = x - 1\) là \(\int\limits_0^3 {\left( { - {x^2} + 4x - 3} \right)dx} \).
b) \({S_1} = \frac{4}{3}\).
c) \({S_1} = {S_2}\).
d) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^2} - 3x + 2,y = x - 1,x = 0,x = 3\) là \(\int\limits_0^3 {\left( { - {x^2} + 4x - 3} \right)dx = 1} \).
PHẦN III. TRẢ LỜI NGẮN
Tính diện tích hình phẳng giới hạn bởi parabol \(y = {x^2} - 4\), trục hoành và hai đường thẳng \(x = 0,x = 3\)(kết quả làm tròn đến hàng phần trăm).
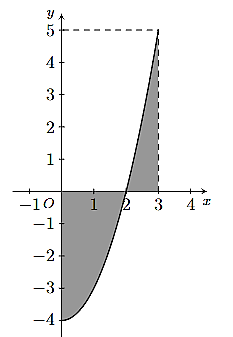
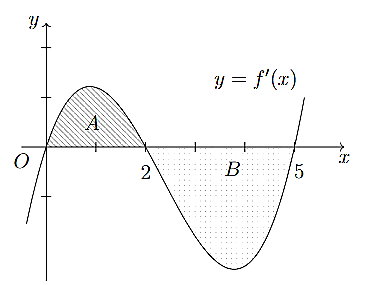
Cho hàm số \(y = f\left( x \right)\). Đồ thị của đạo hàm \(f'\left( x \right)\) là đường cong trong hình dưới. Biết rằng diện tích của các phần hình phẳng A và B lần lượt là SA = 2 và SB = 3. Cho f(0) = 4. Tính f(5).
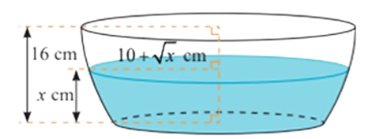
Nếu cắt chậu nước có hình dạng như hình vẽ bằng mặt phẳng song song và cách mặt đáy x (cm), (0 ≤ x ≤ 16) thì mặt cắt là hình tròn có bán kính \(\left( {10 + \sqrt x } \right)\) (cm). Tính dung tích của chậu (kết quả làm tròn đến hàng đơn vị của cm3).
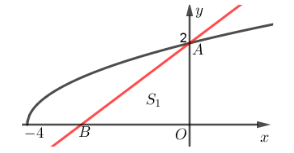
Cho (H) là hình phẳng giới hạn bởi đồ thị hàm số \(y = \sqrt {x + 4} \), trục hoành và trục tung. Biết đường thẳng \(d:ax + by - 16 = 0\) đi qua \(A\left( {0;2} \right)\) và chia (H) thành hai phần có diện tích bằng nhau. Tính \(a + b\).
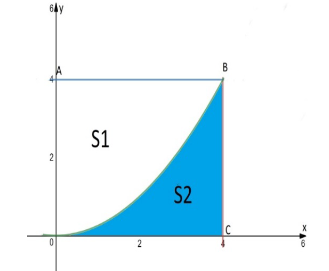
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi đường cong (C) có phương trình \(y = \frac{1}{4}{x^2}\). Gọi \({S_1},{S_2}\) lần lượt là diện tích của phần không tô màu và tô màu như hình. Tính tỉ số \(\frac{{{S_1}}}{{{S_2}}}\).