25 CÂU HỎI
Mặt phẳng (AB'C') chia khối lăng trụ ABC.A'B'C' thành các khối đa diện nào?
A. Một khối chóp tam giác và một khối chóp ngũ giác.
B. Một khối chóp tam giác và một khối chóp tứ giác
C. Hai khối chóp tam giác
D. Hai khối chóp tứ giác
Cho và Khẳng định nào dưới đây là đúng?
A.
B.
C.
D.
Cho cấp số nhân , biết và tổng hai số hạng đầu bằng 3. Tìm công bội q của cấp số nhân trên.
A. q = 4
B.
C. q = -4
D.
Trọng tâm các mặt của một hình tứ diện đều tạo thành một hình đa diện mới có tên là gì

A. Tứ diện đều
B. lập phương
C. nhị thập diện đều
D. bát diện đều
Cho khối lăng trụ đứng có chiều cao là h, đáy là tam giác vuông. Nếu tăng mỗi cạnh góc vuông lên k lần thì thể tích của khối lăng trụ tăng lên bao nhiêu lần?
A.
B.
C.
D.
Số điểm cực trị của hàm số là:
A. 0
B. 1
C. 2
D. 3
Cho bài toán: “Xét tính đơn điệu của hàm số ” Một bạn học sinh đã làm bài như sau:
Bước 1: Tập xác định:
Bước 2: Tìm đạo hàm:
Bước 3:
Bước 4: Bảng biến thiên:

Bước 5: Kết luận:
Vậy hàm số nghịch biến trên nửa khoảng , đồng biến trên nửa khoảng . Hỏi bài làm trên đúng hay
sai? Nếu sai thì sai từ bước nào?
A. Bài làm đúng.
B. Sai từ bước 3.
C. Sai từ bước 4.
D. Sai từ bước 5
Cho số thực và hàm số
Xét 2 phát biểu sau:
(i). Hàm số chắc chắn liên tục từng khoảng .
(ii). Tồn tại số thực a để hàm số liên tục trên R.
Khẳng định nào dưới đây là đúng?
A. (i), (ii) đều đúng
B. (i) sai, (ii) đúng
C. (i) đúng, (ii) sai
D. (i), (ii) đều sai
Cho hàm số y = f(x) liên tục trên R, có đồ thị của đạo hàm f'(x) như sau:
Hỏi mệnh đề nào sau đây là đúng?

A. Hàm số đồng biến trên khoảng .
B. Hàm số nghịch biến trên khoảng .
C. Hàm số đồng biển trên khoảng
D. Hàm số đồng biến trên khoảng (-1;1)
Cho hàm số y = f(x) liên tục trên R , có đồ thị của đạo hàm f'(x) như sau:
Trong các mệnh đề sau, mệnh đề nào sai?
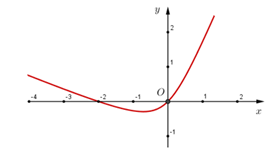
A. f đạt cực tiểu tại x = 0
B. f đạt cực tiểu tại x =-2
C. f đạt cực đại tại x = -2
D. Cực tiểu của f nhỏ hơn cực đại
Tìm giá trị lớn nhất của hàm số trên .
A.
B.
C.
D.
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a, gọi là góc giữa hai mặt phẳng . Tính
A.
B.
C.
D.
Cho tứ diện OABC có OA, OB, OC, OD đôi một vuông góc nhau, biết rằng . Tính khoảng cách d từ O đến mặt phẳng (ABC).
A.
B.
C.
D.
Gọi a là giá trị thực để hàm số liên tục tại x = 0. Gía trị gần với số nào nhất dưới đây?
A. 3,32
B. 3,31
C. 3,61
D. 3,92
Gọi là tiếp tuyến của đường cong . Biết rằng qua điểm (-1;0). Tính khoảng cách d từ điểm M(1;-1) đến
A.
B.
C. d = 1
D. d = 2
Cho hình lập phương ABCD.A'B'C'D' có cạnh là a. Tính thể tích khối tứ diện ABC'D' theo a?
A.
B.
C.
D.
Biết rằng mức lương của một kỹ sư ở công ty X trong quý I năm 2017 (3 tháng đầu tiên của năm 2017) là (triệu đồng), kể từ quý II mức lương sẽ được tăng thêm 0,5 triệu đồng mỗi quý. Tổng lương của kỹ sư đó tính từ quý I năm 2017 đến hết quý IV năm 2022 là 1002 (triệu đồng). Tính tổng lương S (triệu đồng) của kỹ sư tính từ quý I năm 2017 đến hết quý IV năm 2015.
A. S = 1611
B. S = 342
C. S = 324
D. S = 1911
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = a, , tam giác SAB đều và nằm trong mặt phẳng vuông góc đáy. Gọi a (độ) là bởi cạnh SB và mặt phẳng (SAB). Gía trị a gần với số nào nhất dưới đây?
A. 30
B. 40
C. 50
D. 60
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau; AB = 3a, AC = 4a, AD = 5a. Gọi M, N, P lần lượt là trọng tâm của tam giác DAB, DBC, DCA. Tính thể tích của khối chóp DMNA theo a.
A.
B.
C.
D.
Cho hình chóp tứ giác đều S.ABCD có AB = a, gọi là góc giữa mặt bên và mặt đáy của hình chóp S.ABCD. Tính khoảng cách d giữa SA và CD theo a và
A. d = a.cos
B. d = a.sin
C. d = a.sin2
D. d = a.cos2
Cho hàm số . Gọi S là tập hợp tất cả các giá trị nguyên của M để hàm số nghịch biến trên khoảng (1;4). Số phần tử của S là:
A. 0
B. 1
C. 2
D. 3
Cho hình lập phương ABCD.A’B’C’D’. I là trung điểm BB’. Mặt phẳng (DIC’) chia khối lập phương thành 2 phần có tỉ số thể tích phần bé chia phần lớn bằng:
A. 1:3
B. 7:17
C. 4:14
D. 1:2
Xét các hàm số và trên đoạn [1;5]. Biết trên đoạn [1;5] thì giá trị lớn nhất của f(x) bằng giá trị nhỏ nhất của g(x) và đạt tại cùng một điểm . Tính S là tổng các giá trị a, b thoả mãn yêu cầu bài toán .
A. S = 0
B. S = -1
C.
D. không tồn tại S
Cho hàm số với m là tham số thực. Gọi S là tập hợp tất cả các giá trị của m sao cho đồ thị hàm số có hai điểm cực trị. Biết rằng khi m thay đổi trong S, các điểm cực đại của đồ thị hàm số cũng thay đổi nhưng luôn nằm trên một đường thẳng (d) cố định . Hỏi (d) song song với đường thẳng nào sau đây:
A. y = 2x + 4
B. y = -3x - 1
C. y = -3x + 5
D. y = -2x
Một nhà địa chất học đang ở tại điểm A trên sa mạc. Anh ta muốn đến điểm B và cách A một đoạn là 70 km. Trong sa mạc thì xe anh ta chỉ có thể di chuyển với vận tốc là 30 km/h. Nhà địa chất ấy phải đến được điểm B sau 2 giờ. Vì vậy, nếu anh ta đi thẳng từ A đến B sẽ không thể đến đúng giờ. May mắn thay, có một con đường nhựa song song với đường nối A và B và cách AB một đoạn 10 km. Trên đường nhựa này thì xe của nhà địa chất học này có thể di chuyển với vận tốc 50 km/h. Tìm thời gian ngắn nhất mà nhà địa chất học có thể đi từ A đến B (đảm bảo trong khung giờ cho phép).
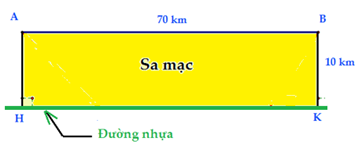
A. 1,83 giờ
B. 1,93 giờ
C. 1,73 giờ
D. 1,86 giờ


