Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 26)
100 câu hỏi
Phần tư duy đọc hiểu
Từ thông tin của bài đọc, hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí tấn công, phạm vi, lãnh thổ, đụng độ, quân sự
Một cuộc nghiên cứu về tinh tinh miền tây ở châu Phi đã hé lộ rằng chúng khôn khéo sử dụng chiến thuật quân sự cổ xưa của con người để tránh xa các cuộc _______ đầy nguy hiểm. Thay vì thụ động, chúng đặt mình ở vị trí cao để cảm nhận và đánh giá tình hình xung quanh, một chiến thuật mà con người từng sử dụng trong _______ cổ đại.
Nghiên cứu của Lemoine đã chứng minh điều gì trong hành vi của tinh tinh ở vườn quốc gia Taï?
Tinh tinh thường tránh địa thế cao trong cuộc xung đột
Tinh tinh sử dụng chiến thuật quân sự để bảo vệ lãnh thổ.
Tinh tinh hiếm khi thể hiện sự nhận thức về môi trường xung quanh.
Nghiên cứu không đưa ra bất kỳ kết luận nào về hành vi của tinh tinh.
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Sự nhận thức phức tạp giúp tinh tinh mở rộng lãnh thổ và chọn lọc tự nhiên đã thúc đẩy chiến thuật chiến đấu của chúng.
Đúng
Sai
Tác giả viết bài văn trên nhằm mục đích gì?
(chọn nhiều đáp án)
Tác giả viết bài văn trên để trình bày kết quả chi tiết một cuộc nghiên cứu về hành vi của tinh tinh.
Tác giả viết bài để phản đối và bác bỏ những nghiên cứu trước đó về hành vi của tinh tinh.
Tác giả mô tả các chiến thuật quân sự của tinh tinh nhằm tăng cường sự hiểu biết về tương tác xã hội và sinh học của chúng.
Tác giả muốn giới thiệu về lịch sử và đặc điểm tự nhiên của tinh tinh miền tây Bờ Biển Ngà.
Điền một từ không quá hai tiếng có trong bài đọc vào chỗ trống
Nghiên cứu của Lemoine không chỉ mở ra cái nhìn mới về chiến thuật quân sự của tinh tinh miền tây mà còn nhấn mạnh tầm quan trọng của khả năng _______ của chúng trong việc phát triển chiến thuật chiến đấu.
Thông tin nào KHÔNG thể suy ra từ những gì tác giả trình bày?
Chiến thuật của tinh tinh không thay đổi tùy thuộc vào số lượng cá thể trong mỗi bên.
Các nhà nghiên cứu đã thu thập dữ liệu hành vi của bầy tinh tinh trung bình 10 giờ mỗi ngày trong suốt 3 năm.
Đàn tinh tinh không đánh dấu lãnh thổ mà trực tiếp có mặt để bảo vệ tài nguyên đất đai.
Lemoine và các cộng sự lạc quan với kết quả của nghiên cứu, tin rằng chúng có thể áp dụng với những bầy tinh tinh khác.
Từ thông tin của bài đọc, hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí.
tự động hóa, tối ưu hóa, tận dung, sử dụng
Có vẻ như tinh tinh miền tây không chỉ sử dụng chiến thuật quân sự để đảm bảo an toàn cho bản thân mà còn để _______ cơ hội sinh tồn. Việc chúng có thể _______ địa thế cao để ngồi yên và quan sát, sau đó quyết định liệu nên tấn công hay không, là một biểu hiện rõ ràng của khả năng đánh giá tình hình xung quanh.
Điền một từ không quá hai tiếng có trong bài văn vào chỗ trống.
Tập tính tự nhiên là kết quả của quy luật tương tác phức tạp giữa các yếu tố môi trường, đóng góp vào sự đa dạng của hệ sinh thái và quá trình_______
Nghiên cứu tại Bờ Biển Ngà của Lemoine đã làm thay đổi quan điểm chúng ta về gì trong lĩnh vực hành vi động vật?
(chọn nhiều đáp án)
Chúng ta hiểu rõ hơn về sự nguy hiểm của tinh tinh trong môi trường sống tự nhiên.
Chiến thuật quân sự là một khía cạnh quan trọng của hành vi động vật.
Nghiên cứu chỉ chứng minh sự giống nhau giữa tinh tinh và con người trong chiến thuật.
Chúng ta có cái nhìn mới về khả năng nhận thức và chiến thuật của tinh tinh.
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Sự cân bằng quyền lực không có ảnh hưởng đến bạo lực trong cuộc xung đột của hai bầy tinh tinh.
Đúng
Sai
Nội dung có thể suy ra từ truyện ngắn trên là:
(chọn nhiều đáp án)
Sự đối mặt với quá khứ.
Sự đồng cảm và lo lắng.
Sự đổi thay của tính cách con người.
Sự ngẫu nhiên và bất ngờ
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Ý nghĩa của truyện ngắn có thể được hiểu thông qua những tình huống và cảm xúc mà người kể chuyện trải qua trong suốt chuyến bay.
Đúng
Sai
Từ thông tin của bài đọc, hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí.
việc làm, lao động, thực tế, tinh tế, quen thuộc gần gũi
Truyện ngắn kể về một chuyến bay của người kể chuyện, trong đó anh gặp một cô gái trẻ chuẩn bị đi xuất khẩu _______. Trong chuyến bay, anh nhận ra một người đàn ông _______ ngồi ở dãy ghế bên cạnh, khiến anh sững sờ và đau lòng khi nhớ về quá khứ. Những khía cạnh như sự ngẫu nhiên, sự đồng cảm, và khả năng đối mặt với quá khứ con người được tác giả _______ miêu tả.
Cô gái trẻ chuẩn bị đi xuất khẩu lao động đã học xong lớp mấy và đã trượt đại học bao lâu?
Lớp 10, trượt hai năm đại học
Lớp 12, trượt hai năm đại học
Lớp 11, trượt một năm đại học
Lớp 12, trượt ba năm đại học
Điền một từ không quá hai tiếng có trong đoạn [3] vào chỗ trống:
Trong cuộc hội thoại với cô gái trẻ, tôi bắt đầu ______ một kịch bản bảo vệ để giúp cô bé tránh xa khỏi những rủi ro có thể xảy ra khi cô vừa mới đến Hà Nội.
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Người đàn ông ngồi bất động trong máy bay đã quay đầu để nhìn thẳng vào tác giả khi bị nhận ra.
Đúng
Sai
Từ thông tin của bài đọc, hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí
vui mừng, trò chuyện, lo lắng, xuất hiện, hội ngộ
Tình huống chính trong truyện này là cuộc _______ bất ngờ giữa người kể chuyện và một người quen từ quá khứ trong suốt chuyến bay từ thành phố Hồ Chí Minh về Hà Nội. Người quen này là một người đàn ông mà người kể chuyện đã biết từ trước, và sự _______ của ông ta khiến nhân vật chính nhớ lại nhiều kỉ niệm ngày xưa.
Người thanh niên trong truyện mặc trang phục và đồ trang sức nào?
Quân phục và dây chuyền vàng
Đồng phục công an và bảng hiệu
Áo vàng, mũ cát vàng, không đeo đồ trang sức
Không mặc trang phục nào và không đeo đồ trang sức nào
Qua truyện ngắn trên, có thể rút ra điều gì về phong cách sáng tác của Nguyễn Minh Châu?
(chọn nhiều đáp án)
Chú trọng miêu tả cảnh vật và trần thuật bên ngoài câu chuyện.
Tập trung vào nhân vật và các mối quan hệ giữa người với người.
Đề cao khía cạnh nhân văn trong mối quan hệ con người.
Xây dựng tình huống truyện phức tạp tạo tiền đề phát triển câu chuyện.
Điền một từ không quá hai tiếng có trong bài văn vào chỗ trống.
Người đàn ông ngồi bất động trên máy bay tỏ ra có vẻ ________, ánh mắt chằm chằm nhìn về phía trước, toát lên một vẻ tự hào và không chịu chuyển động.
Phần tư duy khoa học / giải quyết vấn đề
Nhận định nào dưới đây đúng hay sai?
Các loài sử dụng nguồn thức ăn khác nhau nhưng cấu tạo cơ quan tiêu hóa đều giống nhau.
Đúng
Sai
Loài động vật nào dưới đây có răng phân hóa thành răng cửa, răng nanh, răng ăn thịt và răng hàm và dạ dày đơn?
Trâu.
Sư tử.
Hươu.
Thỏ.
Ở động vật ăn thịt, loại răng nào kém phát triển nhất?
Răng nanh.
Răng ăn thịt.
Răng hàm.
Răng cửa.
Chọn các đáp án chính xác
Những động vật nào sau đây có dạ dày đơn?
Trâu.
Bò.
Báo đốm.
Ngựa.
Nai
Kéo đáp án chính xác vào chỗ trống.
dạ cỏ, dạ tổ ong, dạ lá sách, dạ múi khế
Ở thực vật nhai lại, hệ vi sinh vật phân giải xenlulozo và chuyển hóa thành protein nằm ở _______ trong dạ dày 4 túi.
Điều gì giúp động vật nhai lại nghiền nát thức ăn?
Hàm trên có tấm sừng thay cho răng cửa và răng nanh.
Răng ăn thịt rất phát triển.
Hàm dưới có răng cửa phát triển hơn răng nanh.
Răng trước hàm và răng hàm có các gờ xi măng nổi trên bề mặt.
Điểm giống nhau của cơ quan tiêu hóa ở nai và thỏ?
Dạ dày đơn.
Ruột ngắn và mạnh tràng phát triển.
Hệ vi sinh vật cộng sinh phát triển.
Dạ dày 4 túi.
Cho hình vẽ về bó cơ của chân. Lực ở gân Achilles bằng bao nhiều nếu người chơi chỉ đứng bằng một chân? Coi tất cả các xương bàn chân là một khối cứng (hình B). Bỏ qua trọng lượng của xương bàn chân và g = 9,81m/s2
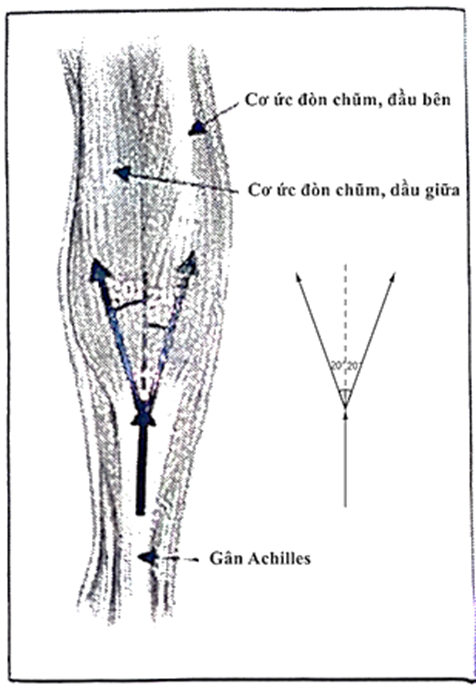
1,35.103N
2,52.103N
1,83.103N
1,28.103N
Tính lực căng riêng của cơ bắp chân.
7,96.105 N/m2
7,96.103 N/m2
7,65.105 N/m2
6,79.105 N/m2
Điền số thích hợp vào chỗ trống:
Nếu hai cơ ức đòn chũm (đầu bên và đầu giữa) phân bổ như nhau vào tổng 60% lực tác động lên gân Achilles). Lực căng do hai cơ này tác động vào gân (lấy phần nguyên) là _______ N
Đối với một cầu thủ bóng đá khỏe mạnh, xương chày có thể chịu được một lực tối đa là 3,60N trên 4,90.102 (mm2) trước khi gãy. Trong một trận bóng, cầu thủ A không may sút trúng cầu thủ B. Kết quả là cầu thủ B bị trấn thương ở xương chày (giả sử xương chày của cầu thủ B đứng yên trước va chạm). Sau va chạm, chân cầu thủ B chuyển động trở lại với vận tốc 4,25m/s. Khối lượng của chân anh ta là 3,20kg và thời gian va chạm là 55,0ms và diện tích va chạm 6,20.102 mm2, biết không có ngoại lực nào khác ảnh hưởng đến chân của cầu thủ B. Khi đó lực tác dụng lên xương chày của B là bao nhiêu?
127N
247N
174N
256N
Chọn đúng hoặc sai cho các nhận xét sau:
Phát biểu | ĐÚNG | SAI |
Xương chày của cầu thủ B bị gãy. | ||
Xương chày của cầu thủ B không gãy. |
Nhiều công ti thể thao phát triển miếng đệm ống chân. Miếng đệm có tác dụng hấp thụ tác động có nguy cơ gây ra thương tích khi va chạm trong các trận đấu bóng đá. Trong một thử nghiệm để so sánh hiệu quả các nhãn hiệu đệm ống khác nhau, mỗi miếng đệm của ống chân bọc ngoài một thiết bị mô phỏng xương chày của người. Mỗi thiết bị đá (tác động) được sử dụng để bắt chước chân của một cầu thủ tấn công. Một đồng hồ đo lực được đặt bên dưới miếng đệm để đo lực tác động lên xương chày. Bảng sau thể hiện kết quả:
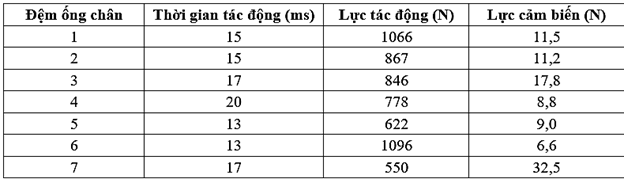
Lực hấp thụ của tấm đệm càng _______ thì tấm đệm đó càng tốt.
Thứ tự sắp xếp các đệm trên theo thứ tự giảm dần của khả năng hấp thụ lực cao nhất trên một đơn vị thời gian là?
6 – 1 – 2 – 3 – 5 – 4 - 7
6 – 1 – 3 – 5 – 4 – 7 - 2
2 – 6 – 1 – 3 – 5 – 4 - 7
5 – 2 – 6 – 3 – 1 – 4 – 7
Cho phản ứng: 2NOCl(g) → 2NO(g) + Cl2(g) . Năng lượng hoạt hóa của phản ứng này là 100 kJ/mol. Ở 350K, hằng số tốc độ của phản ứng là 8.10−6 L/(mol.s). Hằng số tốc độ phản ứng của phản ứng này ở 400K là
5,87.10−4 L/mol.s.
4,86.10−4 L/mol.s.
5,78.10−4 L/mol.s.
4,68.10−4 L/mol.s.
Trong những nhận định sau, nhận định nào là nhận định chính xác?
Phát biểu | ĐÚNG | SAI |
Tất cả các phân tử hóa học khi đã xảy ra sự va chạm với nhau thì đều là va chạm có hiệu quả. | ||
Tất cả các phân tử hóa học khi đã xảy ra sự va chạm với nhau thì đều xảy ra phản ứng hóa học. | ||
Năng lượng hoạt hóa của một phản ứng hóa học càng lớn thì phản ứng hóa học đó càng dễ xảy ra. | ||
Khi Ea càng lớn thì k càng nhỏ, tốc độ phản ứng càng nhỏ. |
Kéo thả đáp án thích hợp vào chỗ trống:
Cl, O3, ClO, O2
Sự suy giảm tầng ozone và lỗ thủng tầng ozone (O3) đã gây ra mối lo ngại về việc gia tăng nguy cơ ung thư da, cháy nắng, mù mắt và đục thủy tinh thể,… Tầng ozone hấp thụ hầu hết các tia cực tím (UV) có hại cho sự sống trên Trái Đất. Các phân tử ozone có thể bị phá hủy theo hai giai đoạn:
Cl + O3 → ClO + O2 và ClO + O3 → Cl + 2O2
Chất xúc tác trong quá trình này là _______.
Thực nghiệm cho biết phản ứng 2N2O5(g) → 4NO2(g) + O2(g) ở 45oC có hằng số tốc độ phản ứng là 8,17.10−3s−1; Ea = 103,5 kJ/mol. Hằng số tốc độ phản ứng tại 65oC là
0,082.
0,083.
0,084.
0,085.
Một phản ứng đơn giản xảy ra ở nhiệt độ 100oC, trong điều kiện có xúc tác và không có xúc tác, năng lượng hoạt hóa của phản ứng lần lượt là: Ea1 = 25 kJ/mol, Ea2 = 50 kJ/mol. Nhận định dưới đây là đúng hay sai?
Khi năng lượng hoạt hóa giảm từ 50 kJ/mol về 25 kJ/mol, tốc độ phản ứng tăng 2050 lần.
Đúng
Sai
Chọn nhận định sai trong những nhận định dưới đây?
Khi tăng nhiệt độ của phản ứng thì tốc độ phản ứng tăng.
Khi giảm nhiệt độ của phản ứng thì tốc độ phản ứng giảm.
Tăng nhiệt độ của phản ứng làm giảm năng lượng hoạt hóa của phản ứng nên làm tăng tốc độ phản ứng.
Tăng nhiệt độ của phản ứng làm tăng số va chạm có hiệu quả của các phân tử hóa học là tăng tốc độ phản ứng.
Cơ chế điều hòa mức độ xoắn của NST là cơ chế điều hòa hoạt động gen của sinh vật nhân thực ở cấp độ nào?
Trước phiên mã.
Sau phiên mã.
Trước dịch mã.
Sau dịch mã.
Kéo thả cụm từ chính xác vào chỗ trống: cần ít năng lượng, cần nhiều năng lượng
Điều hòa hoạt động gen ở mức độ trước phiên mã ở sinh vật nhân thực là hình thức điều hòa _______
Chọn những nhận định chính xác.
Sự điều hòa biểu hiện của gen ở mức độ trước phiên mã của sinh vật nhân sơ dựa trên cơ sở khoa học nào?
Các gen nằm trong vùng dị nhiễm sắc của NST không được biểu hiện.
Các gen nằm trong vùng dị nhiễm sắc của NST sẽ được biểu hiện.
Các gen nằm trong vùng nguyên nhiễm sắc của NST không được biểu hiện.
Các gen nằm trong vùng nguyên nhiễm sắc của NST sẽ được biểu hiện.
Đối với cơ chế cải biến histone, hoạt động nào dẫn đến sự ức chế quá trình phiên mã của gen?
Sự gắn nhóm methyl vào histone.
Sự gắn nhóm photphat vào các axit amin trên phân tử histone.
Sự gắn nhóm methyl vào các bazo nito.
Sự gắn nhóm acetyl vào các phân tử lysine của đuôi histone.
Điền từ chính xác vào chỗ trống
Quá trình Acetyl hóa đuôi histone là sự gắn nhóm Acetyl vào các phân tử lysine tích điện _______ của đuôi histone làm giãn xoắn NST.
Quá trình nào dưới đây liên quan đến quá trình biệt hóa tế bào?
Quá trình gắn Acetyl hóa.
Quá trình methyl gắn vào histone.
Quá trình mythyl hóa ADN.
Quá trình photphat hóa.
Nhận định dưới đây đúng hay sai?
Một đoạn ADN có một gen bị bất hoạt do methyl hóa, sau khi diễn ra quá trình nhân đôi ADN, gen bị bất hoạt trên ở ADN con chuyển sang trạng thái hoạt động.
Đúng
Sai
Điền từ/cụm từ thích hợp vào chỗ trống:
Khi sóng điện từ gặp anten _______ thì nó sẽ tạo ra dòng điện cảm ứng biến thiên với cùng ______ với sóng.
Dao động điện từ trong mạch chọn sóng của máy thu khi máy thu bắt sóng là:
Dao động tự do với tần số bằng tần số riêng của mạch
Dao động cưỡng bức có tần số bằng tần số riêng của mạch
Dao động tắt dần có tần số bằng tần số riêng của mạch
Cả 3 câu trên đều sai
Chọn các nhận xét đúng khi nói về nguyên tắc phát và thu sóng điện từ.
Không thể có một thiết bị vừa thu vừa phát sóng điện từ
Để thu sóng điện từ cần dùng một ăng ten
Nhờ có ăng ten mà ta có thể chọn lọc được sóng cần thu
Để phát sóng điện từ phải mắc phối hợp một máy dao động điều hoà với một ăng ten
Kéo thả các từ sau để hoàn thành quá trình thu sóng điện từ trong máy thu thanh
tách sóng, chọn sóng, khuếch đại cao tần, chuyển thành sóng âm, khuếch đại âm tần, chuyển thành sóng hạ âm
Các giai đoạn thu sóng điện từ trong máy thu thanh là: _______ - _______ - _______ - _______ - _______
Trong “máy bắn tốc độ“ xe cộ trên đường:
Chỉ có máy phát sóng vô tuyến
Chỉ có máy thu sóng vô tuyến
Có cả máy phát và thu sóng vô tuyến
Không có máy phát và thu sóng vô tuyến
Tại Hà Nội, một máy đang phát sóng điện từ. Xét một phương truyền có phương thẳng đứng hướng lên. Vào thời điểm t, tại điểm M trên phương truyền, véctơ cảm ứng từ đang có độ lớn cực đại và hướng về phía Nam. Khi đó véctơ cường độ điện trường có
Độ lớn cực đại và hướng về phía Tây
Độ lớn cực đại và hướng về phía Đông
Độ lớn bằng không
Độ lớn cực đại và hướng về phía Bắc
Bước sóng điện từ mà mạch phát hoặc thu được xác định bằng công thức: \(\lambda = cT = \frac{c}{f} = 2\pi c\sqrt {LC} \). Mạch dao động của một máy thu vô tuyến gồm cuộn cảm L = 5μH và tụ xoay có điện dụng biến thiên từ \({C_1} = 10pF \to {C_2} = 250pF\). Dải sóng điện từ mà máy thu được có bước sóng là:
15,5 m đến 41,5 m
13,3 m đến 66,6 m
13,3 m đến 92,5 m
11 m đến 75 m
Nhận định dưới đây là đúng hay sai?
Phản ứng phân rã Uranium là một phản ứng hóa học.
Đúng
Sai
Điền số thích hợp vào chỗ trống (Lấy kết quả đến chữ số thập phân thứ hai)
Biết Uranium còn có một đồng vị nữa là 234U. Nguyên tử khối trung bình của Uranium là _______ amu.
Phản ứng nào dưới đây mô tả chính xác phóng xạ β?
\(_Z^AX \to _2^4{\rm{He}} + _{Z - 2}^{A - 4}X'\).
\(_Z^AX \to _{ - 1}^0e + _{Z + 1}^AX'\).
\(_Z^AX \to _{ + 1}^0e + _{Z - 1}^AX'\).
\(_Z^AX \to _Z^Ae + \gamma \).
Dãy nào dưới đây là kí hiệu hóa học của các hạt theo thứ tự α, β, β+?
\(_2^4{\rm{He}},\,\,_{ - 1}^0e,\,\,_{ + 1}^0e\).
\(_2^4{\rm{He}},\,\,_{ + 1}^0e,\,\,_{ - 1}^0e\).
\(_{ - 1}^0e,\,\,_{ + 1}^0e,\,\,_2^4{\rm{He}}\).
\(_{ + 1}^0e,\,\,_{ - 1}^0e,\,\,_2^4{\rm{He}}\).
Các nhận định dưới đây là đúng hay sai?
Phát biểu | ĐÚNG | SAI |
Khả năng đâm xuyên của các tia phóng xạ có thể sắp xếp theo thứ tự là: γ < β < α. | ||
Khả năng gây ion hóa của các tia phóng xạ có thể sắp xếp theo thứ tự là: γ < β < α. | ||
Không phải phản ứng hạt nhân nào cũng tạo ra phóng xạ γ. |
Nguyên tố nào được tạo ra trong phản ứng hạt nhân dưới đây?
\(_0^1n\,\, + \,\,_{92}^{235}U \to ?\,\, + \,\,_{36}^{92}Kr\,\, + \,\,3_0^1n\)
\(_{56}^{141}{\rm{Ba}}\).
\(_{56}^{142}{\rm{Ba}}\).
\(_{55}^{141}{\rm{Ce}}\).
\(_{55}^{142}{\rm{Ce}}\).
Phần tư duy toán học
Cho hàm số \[y = f\left( x \right)\;\] và \[y = g\left( x \right)\;\] xác định và có đạo hàm trên các khoảng (a;b) và (c,d)
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
Phát biểu | ĐÚNG | SAI |
Nếu hàm số \(f\left( x \right)\) đồng biến trên các khoảng \(\left( {a;b} \right)\) và \(\left( {c;d} \right)\) thì hàm số \(f\left( x \right)\) đồng biến trên khoảng \(\left( {a;b} \right) \cup \left( {c;d} \right)\) | ||
Nếu hàm số \(f\left( x \right)\) đồng biến trên khoảng \(\left( {a;b} \right)\) thì hàm số \(\frac{1}{{f\left( x \right)}}\) đồng biến trên khoảng \(\left( {a;b} \right)\) | ||
Nếu hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( {a;b} \right)\) và hàm số \(y = g\left( x \right)\) nghịch biến trên khảng \(\left( {a;b} \right)\) thì hàm số \(f\left( x \right) - g\left( x \right)\) đồng biến trên khoảng \(\left( {a;b} \right)\) |
Cho \(\int\limits_0^1 {f\left( x \right)dx} = 6;\,\,\int\limits_0^4 {f\left( x \right)dx = 3} \).
Tính \(\int\limits_1^4 {f\left( x \right)dx} \).
Đáp án: _______
Phương trình \({x^3} - 3{x^2} + m = 0\) có ba nghiệm phân biệt khi và chỉ khi \(m\) thuộc khoảng:
\(\left( { - 4;0} \right)\)
\(\left( {0;4} \right)\).
\(\left( { - \infty ;0} \right)\)
\(\left( {0; + \infty } \right)\)
Cho hàm số \(f\left( x \right) = \frac{{{9^x}}}{{{9^x} + 3}}\). Giá trị của biểu thức \(f\left( {\frac{1}{{2022}}} \right) + f\left( {\frac{2}{{2022}}} \right) + \cdots + f\left( {\frac{{2021}}{{2022}}} \right)\) bằng
\(\frac{{2021}}{2}\).
1010 .
1009 .
\(\frac{{4045}}{4}\).
Cho hàm số \(f\left( x \right) = {e^{{x^3} - 2x + 1}}.\left( {9{x^2} - 6} \right)\). Tính \(\int\limits_0^1 {f\left( x \right)dx} \):
3 − e
3 − 3e
e − 3
1 − 3e
Biết điểm \(M\left( {4; - 1} \right)\) là điểm biểu diễn số phức \(z\) trên mặt phẳng phức. Khi đó điểm nào sau đây biểu diễn số phức \(w = 1 - \overline z \) ?
\(C\left( { - 3;1} \right)\)
\(A\left( {3;1} \right)\)
\(D\left( { - 3; - 1} \right)\)
\(B\left( {3; - 1} \right)\)
Bạn A có 4 lego và 3 hộp bút để trang trí bàn học. Bạn A muốn xếp chúng thành 1 hàng ngang thẳng hàng sao cho lego và hộp bút xen kẽ nhau.
Hỏi bạn A có bao nhiêu cách xếp?
Đáp án: _______
Cho hàm số \(y = 7 - 2{\rm{cos}}\left( {x + \frac{\pi }{4}} \right)\)
Giá trị lớn nhất của hàm số là _______
Cho hàm số \(\mathop {{\rm{lim}}}\limits_{x \to 2} \frac{{f\left( x \right) - 15}}{{x - 2}} = 3.{\rm{\;}}\)
Tính \(\mathop {{\rm{lim}}}\limits_{x \to 2} \frac{{f\left( x \right) - 15}}{{\left( {{x^2} - 4} \right)\left[ {\sqrt {2f\left( x \right) + 6} + 4} \right]}}\).
Đáp án: _______
Gọi \({S_1},{S_2}\) là diện tích hình phẳng giới hạn bởi hàm số \(y = {e^x}\), trục hoành và các đường thẳng \(x = 0;x = {\rm{ln}}4;x = k\,\,(0 < k < {\rm{ln}}4)\) như hình vẽ.
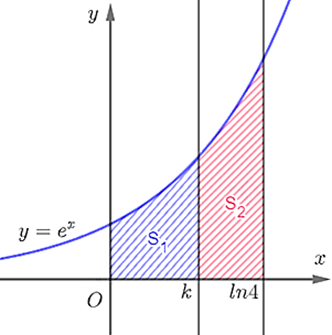Kéo thả các đáp án vào ô trống thích hợp
Với \(k = 1\) thì diện tích \({S_1}\) bằng _______.
Với \(k = 1\) thì diện tích \({S_2}\) bằng _______.
Để \({S_1} = 2{S_2}\) thì giá trị của \(k\) bằng _______.
Giá trị của tổng \(S = 1 + 11 + 111 + \ldots + \underbrace {111...1}_{n\,\,s\`e \,\,1}\) là
\(\frac{1}{{81}}\left( {{{10}^{n - 1}} - 1} \right) - \frac{n}{9}\).
\(\frac{{10}}{{81}}\left( {{{10}^n} - 1} \right) - \frac{n}{9}\).
\(\frac{{10}}{{81}}\left( {{{10}^{n - 1}} - 1} \right) - \frac{n}{9}\).
\(\frac{{10}}{{81}}\left( {{{10}^{n - 1}} - 1} \right) + \frac{n}{9}\).
Cho \(1,\,\,x,\,\,9,\,\,y\) theo thứ tự lập thành một cấp số cộng.
Khi đó: x = _______; y = _______
Điền số thích hợp vào chỗ trống:có tất cả
Số 70560 có tất cả _______ ước nguyên dương.
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \frac{{\left( {x - 2} \right){{(x - 1)}^2}}}{{\sqrt x }}\).Khẳng định nào sau đây là đúng?
Hàm số nghịch biến trên khoảng \(\left( { - \infty ;3} \right)\)
Hàm số đồng biến trên các khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {2; + \infty } \right)\)
Hàm số đồng biến trên các khoảng \(\left( {2; + \infty } \right)\)
Hàm số đồng biến trên khoảng \(\left( {0;2} \right)\) và \(\left( {2; + \infty } \right)\)
Cho \(F\left( x \right)\) là nguyên hàm của \(f\left( x \right) = {\rm{sin}}2x\). Biết \(F\left( 0 \right) = 1\).
Điền các đáp án vào các ô trống sau:
\(F\left( \pi \right) = \)_______
\(F\left( {\frac{\pi }{2}} \right) + \frac{1}{2}F\left( {\frac{\pi }{4}} \right) = \) _______
Có bao nhiêu giá trị nguyên của \({\rm{m}}\) để hàm số \(y = \frac{{mx + 4}}{{x + m}}\) nghịch biến trên khoảng \(\left( { - 1;1} \right)\)?
4
2
5
0
Cho hàm số \(f\left( x \right) = {x^3} - 3x - m\). Tìm \({\rm{m}}\) để mọi bộ ba số phân biệt \({\rm{a}},{\rm{b}},{\rm{c}}\) thuộc đoạn \(\left[ { - 1;3} \right]\) thì \(f\left( a \right),f\left( b \right),f\left( c \right)\) là độ dài ba cạnh của một tam giác.
\(m \le - 22\)
\(m < - 2\)
\(m < 34\)
\(m < - 22\)
Trong một trận chơi golf, xác suất để dùng gậy đánh bóng lọt vào lỗ nhỏ của hai người chơi lần lượt là 54% và 45%. Tính xác suất chỉ có một người có bóng vào lỗ
25,3%
50,4%
29,7%
24,3%
Cho \(a < b < c\), và hàm số \(f\left( x \right)\) có xác định và liên tục trên \(\mathbb{R}\).
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
Phát biểu | ĐÚNG | SAI |
\(\int\limits_a^c {f\left( x \right)dx} - \int\limits_a^b {f\left( x \right)dx} = \int\limits_b^c {f\left( x \right)dx} \) | ||
\({\left( {\int\limits_a^c {f\left( x \right)dx} } \right)^2} = \int\limits_a^c {{{[f\left( x \right)]}^2}dx} \) | ||
\({\left( {\int\limits_a^c {f\left( x \right)dx} } \right)^{\rm{'}}} = \int\limits_a^c {{{[f\left( x \right)]}^{\rm{'}}}dx} \) |
Khối chóp S.ABCD có đáy là hình bình hành. Gọi \({\rm{M}}\) là trung điểm cạnh \(SC\). Mặt phẳng (P) đi qua \({\rm{AM}}\), song song với \({\rm{BD}}\) chia khối chóp thành hai phần. Gọi \({V_1}\) là thể tích khối đa diện có chứa đỉnh S, \({V_2}\) là thể tích khối đa diện còn lại. Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\)?
\(\frac{2}{3}\)
\(\frac{1}{3}\)
\(\frac{1}{2}\)
1
Cho tam giác ABC đều cạnh a nội tiếp đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối nón xoay được tạo thành khi cho phần tô đậm quay quanh đường thẳng AD bằng:
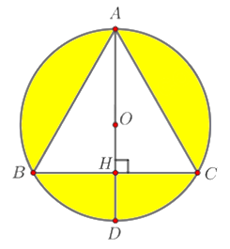
\(\frac{{\pi \sqrt 3 {a^3}}}{{24}}\)
\(\frac{{20\pi \sqrt 3 {a^3}}}{{217}}\)
\(\frac{{4\pi \sqrt 3 {a^3}}}{{27}}\)
\(\frac{{23\pi \sqrt 3 {a^3}}}{{216}}\)
Trong không gian \(Oxyz\), cho điểm \(A\left( {1;2;4} \right)\) và hai đường thẳng \({d_1}:\frac{x}{1} = \frac{y}{1} = \frac{z}{1}\), \({d_2}:\left\{ {\begin{array}{*{20}{l}}{x = 1 - t}\\{y = 1 + t}\\{z = 2t}\end{array}} \right.\). Đường thẳng \({\rm{\Delta }}\) qua \(A\), vuông góc với \({d_1}\) và cắt \({d_2}\) có phương trình là
\(\frac{{x - 1}}{1} = \frac{{y - 2}}{1} = \frac{{z - 4}}{{ - 2}}\).
\(\frac{{x - 1}}{{ - 2}} = \frac{{y - 2}}{1} = \frac{{z - 4}}{2}\).
\(\frac{{x + 1}}{{ - 5}} = \frac{{y + 2}}{3} = \frac{{z + 4}}{2}\).
\(\frac{{x - 1}}{{ - 5}} = \frac{{y - 2}}{3} = \frac{{z - 4}}{2}\).
Số học sinh khối 12 của một trường học là một số có ba chữ số và khi yêu cầu các em học sinh này xếp thành 16 hàng, 20 hàng hoặc 24 hàng đều nhau thì vừa đủ.
Số học sinh khối 12 của trường đó có thể là số nào sau đây?
640
240
480
520
Trong không gian \(Oxyz\), viết phương trình mặt phẳng \(\left( P \right)\) đi qua các hình chiếu của điểm \(M\left( {3;1;4} \right)\) lên các trục tọa độ \(Ox,Oy,Oz\).
\(4x + 12y + 3z + 12 = 0\)
\(4x - 12y - 3z - 12 = 0\)
\(4x + 12y + 3z = 0\)
\(4x + 12y + 3z - 12 = 0\)
Nếu \(m\) là số nguyên dương, \(a\) và \(b\) chia cho \(m\) có cùng số dư thì ta nói \(a\) đồng dư với \(b\) theo mô đun \({\rm{m}}\), kí hiệu \(a \equiv b\left( {{\rm{mod}}\,\,m} \right)\). Khẳng định nào sau đây đúng?
\({5^5} \equiv 1\left( {{\rm{mod}}\,\,6} \right)\)
\({5^5} \equiv 3\left( {{\rm{mod}}\,\,6} \right)\)
\({5^5} \equiv 5\left( {{\rm{mod}}\,\,6} \right)\)
\({5^5} \equiv 0\left( {{\rm{mod}}\,\,6} \right)\)
Đánh số trang của một quyển sách từ trang 1 đến trang 2023.
Cần dùng _______ chữ số để đánh số trang của quyển sách đó.
Đọc các khẳng định sau:
Khẳng định nào đúng, khẳng định nào sai?
Phát biểu | ĐÚNG | SAI |
Hệ số của \({x^5}\) trong khai triển \({(1 + x)^{12}}\) là 792 . | ||
Số tự nhiên \(n\) thỏa mãn \(A_n^2 = 210\) là một số chính phương. |
Một sợi dây kim loại dài 60 cm được cắt thành 2 đoạn. Đoạn thứ nhất uốn thành hình vuông cạnh a, đoạn thứ hai uốn thành đường tròn bán kính r. Để tổng diện tích hình vuông và hình tròn là nhỏ nhất thì tỉ số \(\frac{a}{r}\) bằng
1.
3.
4.
2.
Gọi \(M\) là điểm biểu diễn số phức \(z\) thỏa mãn \(3\left| {z + i} \right| = \left| {2\overline z - z + 3i} \right|\). Tập hợp tất cả các điểm \(M\) như vậy là
một đường tròn
một parabol
một đường thẳng
một elip
Cho đường thẳng \({\rm{\Delta }}\) là tiếp tuyến của đồ thị \(\left( C \right):y = {x^3} + 3{x^2} - 6x + 1\) sao cho \({\rm{\Delta }}\) đi qua điểm \(M\left( {0;1} \right)\).
Điền số thích hợp vào chỗ trống:
Khi đó, có ______ đường thẳng Δ thỏa mãn yêu cầu bài toán.
Có 13 học sinh của một trường THPT đạt danh hiệu học sinh xuất sắc, trong đó khối 12 có 8 học sinh nam và 3 học sinh nữ, khối 11 có 2 học sinh nam. Chọn ngẫu nhiên 3 bạn bất kì lên trao thưởng. Xác suất để 3 học sinh được chọn có cả nam và nữ đồng thời có cả khối 11 và khối 12 là
\(\frac{{57}}{{286}}\).
\(\frac{{24}}{{143}}\)
\(\frac{{27}}{{143}}\)
\(\frac{{229}}{{286}}\).
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông cân tại \(A\). Biết \(AB = 1\), góc giữa \(A'C\) và \(\left( {ABC} \right)\) bằng \({60^ \circ }\).
Kéo các ô sau đây thả vào vị trí thích hợp để được phát biểu đúng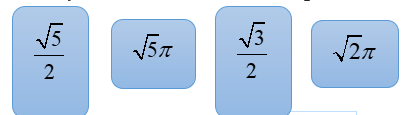
Thể tích khối lăng trụ đã cho bằng _______.
Diện tích mặt cầu ngoại tiếp hình chóp C′.ABB′A′ là _______.
Cho một đồng hồ cát như hình bên dưới (gồm 2 hình nón chung đỉnh ghép lại), trong đó đường sinh bất kì của hình nón hợp với đáy một góc 600.
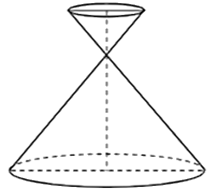
Biết rằng chiều cao của đồng hồ là 30 cm và tỉ lệ thể tích giữa phần lớn và phần nhỏ bằng 8. Thể tích cát (lấy gần đúng đến hàng đơn vị) để đổ đầy phần nhỏ của đồng hồ cát bằng
350 cm3.
349 cm3.
348 cm3.
347 cm3.
Trong không gian \(Oxyz\), cho đường thẳng \(d:\frac{{x - 2}}{2} = \frac{{y + 1}}{1} = \frac{{z - 1}}{2}\) và mặt cầu \(\left( S \right):{(x - 3)^2} + {(y - 1)^2} + {(z + 1)^2} = 4\). Hai mặt phẳng \(\left( P \right),\left( Q \right)\) chứa đường thẳng \(d\) và tiếp xúc với mặt cầu \(\left( S \right)\) lần lượt tại các tiếp điểm \(M,N\). Độ dài đoạn thẳng \(MN\) biểu diễn dưới dạng \(\frac{{a\sqrt b }}{3}\).
Những khẳng định nào sau đây là đúng?
\(a\) chia hết cho \(b\).
\(a\) và \(b\) nguyên tố cùng nhau.
\(a\) và \(b\) nguyên tố cùng nhau.
Một trong hai số là số chính phương.
Cho 2 số thực dương \(a,b\) thỏa mãn \(\frac{1}{2}{\rm{lo}}{{\rm{g}}_2}a = {\rm{lo}}{{\rm{g}}_2}\frac{2}{b}\).
Giá trị nhỏ nhất của biểu thức \(P = 4{a^3} + {b^3} - 4{\rm{lo}}{{\rm{g}}_2}\left( {4{a^3} + {b^3}} \right)\) được viết dưới dạng \(x - y{\rm{lo}}{{\rm{g}}_2}z\) với \(x,y,z\) đều là các số thực dương lớn hơn 2.
Khi đó tổng \(x + y + z\) có giá trị bằng _______.
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) thỏa mãn: \(\int\limits_0^{\frac{\pi }{4}} {f\left( {{\rm{tan}}x} \right)dx = 4} \) và \(\int\limits_0^1 {\frac{{{x^2}f\left( x \right)}}{{{x^2} + 1}}dx = 2} \). Giá trị của tích phân \(I = \int\limits_0^1 {f\left( x \right)dx} \) bằng
1.
3.
6.
8.
Một cái cổng hình parabol có dạng \(y = - \frac{1}{2}{x^2}\) có chiều rộng \(d = 4m\).
Tính chiều cao \(h\) của cổng (xem hình minh họa)
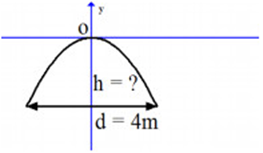
\(h = 8m\).
\(h = 2m\).
\(h = - 2m\).
\(h = 2\sqrt 2 m\).
Cho hàm số \(f\left( x \right) = ax + \frac{b}{{{x^2}}}\). Biết \(F\left( x \right)\) là nguyên hàm của hàm số \(f\left( x \right)\). Biết \(F\left( { - 1} \right) = 2,F\left( 1 \right) = F\left( 2 \right) = 14\). Nguyên hàm \(F\left( x \right)\) là:
\({x^2} - \frac{6}{x} + 7\)
\({x^2} + \frac{6}{x} + 7\)
\({x^2} + 6x + 7\)
\(2{x^2} - \frac{6}{x} + 7\)
Cho hàm số \(y = f\left( x \right)\) thỏa mãn \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{\frac{{\sqrt {mx + 1} - 1}}{x}{\rm{\;khi\;}}x \ne 0}\\{\frac{n}{{30}}\,\,{\rm{khi}}\,\,x = 0}\end{array}} \right.\).
Biết hàm số liên tục tại \(x = 0\).
Khi đó \(\frac{n}{m} = \)_______
Cho số phức \(z\) thỏa mãn điều kiện \(\left| {{z^2} + 4} \right| = \left| {{z^2} + 2iz} \right|\).
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
Phát biểu | ĐÚNG | SAI |
Tập hợp điểm biểu diễn số phức z là một đường thẳng. | ||
Giá trị nhỏ nhất của biểu thức \(P = \left| {z + i} \right|\) là 1 . |
