Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 14)
100 câu hỏi
Theo bài viết, vì sao nhà dân tộc học người Pháp Condominas lại có nhiều công trình nghiên cứu và thành tựu liên quan tới Tây Nguyên?
Vì đây là vùng đất chưa được nhiều người biết tới
Vì ông là một nhà nghiên cứu Dân tộc học đầu tiên.
Vì ông đã phát hiện ra thần linh ẩn hiện ở đây.
Vì ông muốn thực hiện tâm linh của riêng mình.
Đâu là đặc điểm nổi bật để nhận ra nơi ở của những người K’ho?
Cao cẳng và có gầm trống chăn nuôi gia súc.
Làm bằng gỗ và cất sát mặt đất.
Có không gian hoang vắng và đơn sơ.
Được mời uống nước khi đến nhà.
Trong bài viết, tác giả đã nhắc tới tập tục gì của người Kinh?
Quay đầu về hướng bàn thờ của gia đình.
Không nằm quay chân về phía cửa ra vào.
Nằm quay chân vào phía bàn thờ gia tiên.
Quay đầu về hướng cửa chính của gia đình.
Thần linh ở Tây Nguyên được mô tả như thế nào trong bài viết?
Linh hồn các vị thần hiện hữu trong các di tượng.
Thần linh ẩn hiện trong cõi vô hình và ý niệm.
Mỗi vị thần mang đến một niềm tin khác nhau.
Các vị thần trú ngụ trong ngọn cây hay núi sâu.
Ở Tây Nguyên, mỗi vị thần đều bắt nguồn và tồn tại, biến đổi trong tâm thức con người vừa bằng niềm tin vào sức mạnh vừa bằng nỗi sợ vô hình là đúng hay sai?
Đúng
Sai
Nghi thức đầu tiên mà những người Stiêng được tham dự đã gắn với điều gì?
Kỹ năng thổi tai bằng rượu để cầu sức khỏe.
Dùng lời cúng để kết nối với các thần linh.
Bài học về sự lắng nghe trong âm thanh cuộc đời.
Cảm tạ Trời đất đã ban cho đứa trẻ khỏe mạnh.
Tại sao người Stiêng thực hiện nghi lễ Thổi tai?
Để tạo ra tiền đề dựng nên miền huyễn tưởng.
Để chứng giám sự hiện diện của thần linh.
Để chào đón con mới sinh vào cộng đồng.
Để truyền đạt kiến thức về tôn giáo.
Trong nghi lễ Thổi tai của người Stiêng, người già đọc lời cúng trước khi thực hiện nghi thức đổ rượu qua đầu đứa trẻ là đúng hay sai?
Đúng
Sai
Tìm một từ thích hợp (không quá hai tiếng) để hoàn thành câu văn sau:
Trong nghi thức thách cưới của người Stiêng, nhà trai mang đến nhà gái những lễ vật tượng ứng cho rượu, heo, trâu...; đó là những sính lễ chứa đựng (1) ______ của mỗi người và nhờ đó con người chạm vào cõi vô hình, thế giới nơi thần linh trú ngụ.
Nội dung chính của bài viết là gì?
Giới thiệu về lễ hội và nghi lễ thờ thần linh của người Tây Nguyên.
Hành trình khám phá những bí ẩn trong nền văn hóa Tây Nguyên.
Giới thiệu về cuộc sống hàng ngày của người dân K’ho và Stiêng.
Khảo sát những lí thú về tâm linh và tôn giáo ở vùng Tây Nguyên.
Theo đoạn [1], công ti khởi nghiệp muốn biến carbon dioxide thành protein vì không thể loại bỏ lượng khí thải đó trong bầu khí quyển. Đúng hay sai?
Đúng
Sai
Dựa vào đoạn [2], hãy điền một cụm từ không quá hai tiếng để hoàn thành nhận định sau:
Đẩy mạnh những tiến bộ về (1) _____, công ti NovoNutrients đầu tư trang thiết bị kĩ thuật cao, tìm ra cơ sở trong quá trình trao đổi chất của vi khuẩn, sử dụng khí thải làm năng lượng.
Theo đoạn [2], cụm từ “công việc bẩn thỉu” được hiểu như thế nào? Chọn Từ khóa đúng nhất.
Hành động thải khí độc ra tự nhiên, phá hoại môi trường sống.
Nghiên cứu và sử dụng vi khuẩn nhằm tạo ra khí thải carbon dioxide.
Lao động chân tay tại các môi trường mất vệ sinh, không sạch sẽ.
Quá trình sử dụng khí thải làm năng lượng để thực hiện trao đổi chất.
Hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí:
hoạt đồng, đậm đặc, tái tạo, chế tạo
Việc phát triển các lò phản ứng sinh học trở thành yêu cầu cấp thiết và nguyên liệu chính là cacbon dioxide _______- sản phẩm từ bất kì _______ gây ô nhiễm nào trong đời sống và từ đó _______ thành nhiều sản phẩm khác nhau.
NovoNutrients đã làm gì để tăng hiệu suất công việc?
Nghiên cứu và phát triển các chủng vi khuẩn hoang dã, vi khuẩn thích nghi.
Sản xuất bột khô sử dụng trong bể vi khuẩn nhằm tăng giá trị của sản phẩm.
Điều chỉnh dinh dưỡng trong bể bằng cách dùng nhiều chủng vi khuẩn.
Cung cấp đa dạng carbon dioxide đậm đặc trong các lò phản ứng sinh học.
Hãy điền một cụm từ không quá ba tiếng để hoàn thành nhận định sau:
Bên cạnh các mục tiêu thương mại, NovoNutrients hướng tới việc cung cấp (1) _____ cho các doanh nghiệp và đào tạo quy trình hoạt động cho những cơ sở có nhu cầu sử dụng công nghệ này.
Công ti NovoNutrients KHÔNG cung cấp cho đối tác những dịch vụ nào?
Sản phẩm sinh học và phần cứng của công nghệ.
Quy trình đào tạo đội ngũ nhân viên vận hành.
Quyết định sử dụng công nghệ cùng các đối tác.
Trang thiết bị kĩ thuật được cung cấp bởi đối tác.
Hãy hoàn thành các câu sau đây bằng cách kéo thả các từ vào đúng vị trí:
công nghệ, thu mua, cung cấp, tiêu dùng
Công ti NovoNutrients lấy _______ làm trung tâm và cấp phép cho công nghệ cốt lõi của mình. Với vai trò là một công ti _______ dịch vụ, NovoNutrients tư vấn cho các công ti đối tác về quy trình xây dựng, vận hành và hỗ trợ tiếp cận người _______.
Theo thông tin trong đoạn [6], các công ti khởi nghiệp gặp thất bại chủ yếu vì:
Chiến lược phát triển không thực sự phù hợp.
Sản phẩm được sáng chế thiếu tính cạnh tranh.
Các nhà máy sản xuất thiếu đồng bộ công nghệ.
Thiếu động lực trong việc phát triển kinh doanh.
Mục đích chính của bài viết là gì?
Lí giải nguyên nhân và đề xuất việc loại bỏ khí CO2 trong khí quyển.
Giải pháp giảm thải khí CO2 khỏi khí quyển của công ti NovoNutrients.
Giới thiệu mô hình chuyển hóa CO2 thành chất hữu ích trong đời sống.
Kêu gọi cộng đồng cùng tạo ra nguồn năng lượng mới từ khí thải CO2.
Phần tư duy khoa học, giải quyết vấn đề
Phát biểu sau đây đúng hay sai?
Hai thí nghiệm trên, vi khuẩn đều được nuôi cấy trong môi trường nuôi cấy liên tục.
Đúng
Sai
Dung dịch nuôi cấy vi khuẩn càng đục chứng tỏ
vi khuẩn không có sự sinh trưởng dẫn tới hư hỏng môi trường nuôi cấy.
vi khuẩn bị ức chế sinh trưởng.
vi khuẩn sinh trưởng càng mạnh.
nồng độ dinh dưỡng càng cao.
Nhóm vi khuẩn nào có cùng điều kiện thí nghiệm ở hai thí nghiệm trên?
Nuôi trong điều kiện pH = 3 và nhiệt độ 3℃.
Nuôi trong điều kiện pH = 6 và nhiệt độ 37℃.
Nuôi trong điều kiện pH = 6 và nhiệt độ 60℃.
Nuôi trong điều kiện pH = 9 và nhiệt độ 45℃.
Điền từ/cụm từ vào chỗ trống sau đây:
Khi cạn kiệt chất dinh dưỡng, vi khuẩn sẽ bắt đầu pha (1) ________.
Ở giá trị pH nào quần thể vi khuẩn S. Aureus KHÔNG có sự sinh trưởng?
pH = 3, pH = 5.
pH = 6, pH = 9.
pH = 3, pH = 9.
pH = 5, pH = 6.
Phát biểu nào sau đây là đúng khi nghiên cứu kết quả thí nghiệm của nhóm 1?
Khi nhiệt độ tăng thì tốc độ phát triển của S. Aureus cũng tăng.
Chủng vi khuẩn S. Aureus phát triển tối ưu ở nhiệt độ 37℃.
Khi nhiệt độ giảm, tốc độ phát triển của S. Aureus cũng giảm.
S. Aureus phát triển theo cấp số nhân ở nhiệt độ 37℃.
Phát biểu sau đây đúng hay sai?
Trong thí nghiệm của nhóm 1, ở nhiệt độ 37℃, pha cân bằng có thể bắt đầu sau 10 giờ kể từ khi nuôi cấy.
Đúng
Sai
Khẳng định nào sau đây là đúng? Một động cơ nhiệt hoạt động tốt có nghĩa là
càng nhiều nhiệt lượng nhận từ nguồn nhiệt Q1 chuyển thành công càng tốt.
càng nhiều nhiệt lượng nhận từ nguồn nhiệt Q2 chuyển thành công càng tốt.
càng nhiều nhiệt lượng lấy từ nguồn nhiệt Q1 chuyển sang nguồn nhiệt Q2 càng tốt.
càng nhiều nhiệt lượng lấy từ nguồn nhiệt Q2 chuyển sang nguồn nhiệt Q1 càng tốt.
Phát biểu nào sau đây là đúng hoặc sai?
Phát biểu | Đúng | Sai |
Nhiệt kế rượu được sử dụng để ghi lại sự thay đổi nhiệt độ của không khí trong các thử nghiệm. | ||
Khi thiết bị làm mát được đặt ở chế độ để làm mát nước đến nhiệt độ 10°C thì nhiệt độ của nước thay đổi nhanh nhất trong khoảng thời gian từ 0 – 100 phút. | ||
Trong các thử nghiệm, nhiệt độ thay đổi chậm lúc đầu và nhanh hơn theo thời gian. |
Trong thử nghiệm làm mát nước mặn, khi bộ làm mát của máy lạnh được đặt ở chế độ để làm mát nước đến nhiệt độ 0℃ thì trong 220 phút nhiệt độ của nước là
52℃.
29℃.
17℃.
7℃.
Kéo thả từ/cụm từ vào vị trí thích hợp
phòng cần làm lạnh, không khí bên ngoài, motor của máy lạnh
Trong máy điều hòa không khí, nguồn nhiệt độ thấp là ______, nguồn nhiệt độ cao là ______ và công là do ______ thực hiện.
Kéo thả từ/cụm từ vào vị trí thích hợp:
thấp, cao
Trong tủ lạnh của gia đình, nguồn nhiệt độ _______ là buồng chứa thực phẩm, nguồn có nhiệt độ _______ là phòng, nơi đặt tủ lạnh.
Tủ lạnh của gia đình bạn Hoa có hiệu suất K là 4,7. Tủ lạnh lấy nhiệt từ buồng lạnh với tốc độ 250 J trong mỗi chu trình. Công mà hệ thực hiện được trong một chu trình để nó hoạt động có độ lớn là (1) ________J. (Làm tròn đến chữ số thập phân thứ nhất)
Một động cơ ô tô có hiệu suất nhiệt là 22% chuyển động được 95 chu trình trong thời gian một giây và thực hiện một công là 120 HP. Biết rằng 1HP = 746W. Phát biểu nào sau đây là đúng hoặc sai?
Phát biểu | Đúng | Sai |
Công thực hiện trong mỗi chu trình là 942 J. | ||
Động cơ nhận năng lượng 3340 J trong mỗi chu trình. | ||
Năng lượng mà động cơ thải ra lớn gấp 3,6 lần năng lượng biến thành có ích. |
Phát biểu sau đúng hay sai?
Theo quan điểm của học sinh 3, mẫu A và B được tạo thành từ cùng một chất.
Đúng
Sai
Điền số thích hợp vào chỗ trống
Các số liệu về khối lượng, thể tích và khối lượng riêng của các mẫu A – H trong Bảng 1 được xác định tại nhiệt độ (1) ________ oC.
Dựa vào Bảng 1, mẫu B và C có bao nhiêu tính chất giống nhau?
1 tính chất.
2 tính chất.
3 tính chất.
4 tính chất.
Điền từ/cụm từ thích hợp vào chỗ trống
Giả sử nhiệt độ của mẫu D tăng lên 890°C ở áp suất 1 atm, lúc này mẫu D sẽ chuyển sang thể khí. Khối lượng riêng của mẫu sẽ (1) ________ so với ở 20°C và 1 atm.
Dựa trên lời giải thích của Học sinh 1, hai mẫu nào sau đây được tạo thành từ cùng một chất?
Mẫu A và B.
Mẫu B và C.
Mẫu C và D.
Mẫu D và E.
Cho quan điểm sau: “Hai mẫu có cùng khối lượng, thể tích, khối lượng riêng và điểm sôi được tạo thành từ cùng một chất, ngay cả khi chúng có điểm nóng chảy khác nhau”. Học sinh nào trong số học sinh 2 và 4 sẽ có khả năng đồng ý với ý kiến này?
Học sinh 2.
Học sinh 4.
Cả học sinh 2 và 4.
Không có học sinh nào.
Phân tử nào sau đây có vai trò giúp vi khuẩn kháng penicillin?
Enzyme beta lactamase.
Gen thalassemia.
Alpha-1 antitrypsin.
Gen CFTR.
Saccharose và lactose thuộc nhóm (1) _________.
Tế bào chủng vi khuẩn dạng dại ban đầu có khả năng
kháng penicillin và chuyển hóa được glucose cũng như saccharose.
kháng tetracyclin và chuyển hóa được glucose cũng như saccharose.
chuyển hóa được glucose và saccharose nhưng không kháng kháng sinh.
chuyển hóa được lactose, kháng tetracyclin nhưng không kháng penicillin.
Vai trò của nước thịt trong thí nghiệm trên là
cung cấp oxygen cho vi khuẩn sinh trưởng.
cung cấp carbon cho vi khuẩn sinh trưởng.
cung cấp nitrogen hữu cơ cho vi khuẩn sinh trưởng.
cung cấp enzyme cho vi khuẩn sinh trưởng.
Điền từ/cụm từ thích hợp vào chỗ trống sau đây:
Sự (1) ________ của quần thể vi sinh vật là sự tăng số lượng tế bào trong quần thể.
Kết luận nào dưới đây có thể rút ra từ kết quả thí nghiệm ở bảng 2?
Phage I chèn DNA vào nhiễm sắc thể của vi khuẩn làm cho vách tế bào vi khuẩn không chịu tác động bởi tetracycline.
Phage I làm giảm penicillium trên đĩa thạch do đó cho phép tế bào vi khuẩn sinh trưởng.
Phage I mang gen mã hóa cho beta lactamase.
Phage I ức chế sự phát triển của vi khuẩn.
Phát biểu sau đây đúng hay sai?
Tế bào vi khuẩn dạng dại trong tự nhiên không có khả năng kháng lại cả tetracyclin và penicillin.
Đúng
Sai
Phát biểu sau đúng hay sai?
Phương trình phản ứng xảy ra trong thí nghiệm 2 là: 2H2+O2→2H2O.
Đúng
Sai
Phát biểu sau đúng hay sai?
Sử dụng CuO bị lẫn tạp chất không làm ảnh hưởng đến kết quả của thí nghiệm 2.
Đúng
Sai
Điền từ/cụm từ thích hợp vào chỗ trống.
Trong thí nghiệm 2, nếu CuO phản ứng với H2 để tạo ra các sản phẩm không phải là H2O thì (1) _______ dùng thí nghiệm này để xác định tính đúng đắn của phản ứng: H2 + CuO Cu + H2O.
Điện phân nước thu được hydrogen và oxygen theo phương trình phản ứng
Phát biểu nào sau đây là đúng về phản ứng hóa học trong thí nghiệm 2?
O2 phải dư để hình thành nước.
Chỉ CuO nung nóng mới phản ứng được với H2.
H2O không bị CaCl2 hấp thụ.
H2 và O2 phản ứng theo tỷ lệ 1:2.
Kéo thả vào vị trí thích hợp:
25ml, 25ml, 0ml, 50ml
Nếu thể tích ban đầu của H2 và O2 lần lượt là 50 ml và 50 ml thì thể tích cuối cùng của O2 sau khi phản ứng xảy ra hoàn toàn là _______.
Phát biểu sau đúng hay sai?
Hợp chất hữu cơ X có phần trăm khối lượng của các nguyên tố như sau: %C = 45,80%; %H = 10,57%; %N = 13,24%, còn lại là O. Biết MC =12,01 g/mol, MH = 1,008 g/mol và MO = 16,00 g/mol. Công thức kinh nghiệm của X là C4H10NO2.
Đúng
Sai
Các phát biểu sau đúng hay sai?
Phát biểu | Đúng | Sai |
Công thức phân tử của methyl formate và glucose lần lượt là C2H4O2 và C6H12O6. Công thức kinh nghiệm của hai chất này là CH2O. | ||
Người ta thường xác định tỉ khối của một chất khí X (chưa biết phân tử khối) so với không khí (dX/kk) rồi tính phân tử khối của X theo công thức: MX =26.dX/kk. | ||
Trong phương pháp phổ khối lượng, đối với các hợp chất đơn giản, thường mảnh có giá trị m/z lớn nhất ứng với mảnh ion phân tử [M+] và giá trị này bằng giá trị nguyên tử khối của chất nghiên cứu. |
Điền số thích hợp vào chỗ trống
Cho biết nước có nhiệt độ sôi là 100°C và hằng số nghiệm sôi K là 0,51 (℃.g/mol). Hoà tan 18 g glucose vào 150 g nước thì thu được một dung dịch sôi ở 100,34°C. Khối lượng phân tử của glucose là (1) ______ (g/mol).
Kéo thả các ô vuông vào vị trí thích hợp:
H, HCl, CuSO4 khan, H2O, AgNO3, CO2, C, Cl2O7
Khi đốt cháy hoàn toàn hợp chất hữu cơ thì ______ chuyển thành CO2, ______ chuyển thành ______, Cl chuyển thành ______. Người ta nhận ra trong sản phẩm cháy có ______ nhờ nước vôi trong, nhận ra sự có mặt của H2O nhờ ______, nhận ra HCl nhờ dung dịch ______.
Hoà tan 1,00 mg một protein vào nước thu được 1,00 ml dung dịch rồi đo áp suất thẩm thấu ở 25°C thì được giá trị π = 1,12 mmHg. Phân tử khối của protein đã cho là
1,66.102 (g/mol).
1,66.103 (g/mol).
1,66.104 (g/mol).
1,66.105 (g/mol).
Cho biết benzene có nhiệt độ đông đặc là 5,5°C và hằng số nghiệm lạnh K là 5,12 (℃.g/mol). Xác định phân tử khối của hormone thyroxine? (Biết rằng dung dịch chứa 0,546 g thyroxine trong 15 g benzene đông đặc ở 5,26°C).
384 g/mol.
777 g/mol.
175 g/mol.
388 g/mol.
Lindane là một hóa chất được sử dụng làm thuốc trừ sâu trong nông nghiệp và làm dược phẩm điều trị bệnh ghẻ, diệt chấy,.... Tiếp xúc với một lượng lớn lindane có thể gây hại cho hệ thần kinh, gây ra một loạt các triệu chứng như đau đầu, chóng mặt dẫn đến co giật và hiếm gặp hơn là tử vong. Thành phần phần trăm khối lượng của các nguyên tố có trong lindane là: 24,78% C; 2,08% H và 73,14% Cl. Dựa vào phổ khối lượng, xác định được phân tử khối của lindane là 288 (ứng với 35Cl) hoặc 300 (ứng với 37Cl). Trong tự nhiên, 35Cl chiếm 75,77% số lượng nguyên tử còn 37Cl chiếm 24,23% số lượng nguyên tử. Công thức phân tử của lindane là
C9H12Cl.
C8H8Cl2.
C7H5Cl3.
C6H6Cl6.
Phần tư duy toán học
Một nửa đàn dê đang ăn cỏ trên một cánh đồng và ba phần tư số còn lại đang lang thang gần đó. 9 con còn lại đang nước uống bên bờ hồ.
Mỗi phát biểu sau đây là đúng hay sai?
Phát biểu | Đúng | Sai |
Có 48 con dê đang ăn cỏ trên cánh đồng. | ||
Có 36 con dê đang lang thang gần cánh đồng cỏ. | ||
Đàn dê có 72 con. |
Trong một hội thảo của công ty A gồm 100 người có cơ cấu theo trình độ cán bộ công nhân viên (CBCNV) như biểu đồ dưới đây:
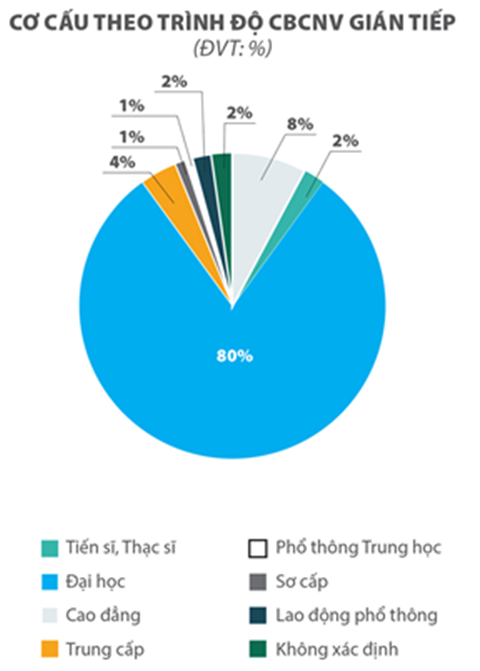
Chọn ra 20 người để nhận phần quà may mắn từ diễn giả của hội thảo. Xác suất để trong 20 người có \(\frac{3}{4}\) số người có trình độ là Đại học là bao nhiêu? (Kết quả làm tròn đến chữ số thập phân thứ hai)
0,19.
0,20.
0,12.
0,21.
Trong mặt phẳng với hệ trục tọa độ Oxy, cho hai số phức \({z_1}\) có điểm biểu diễn \(M\), số phức \({z_2}\) có điểm biểu diễn là \(N\) thỏa mãn \(\left| {{z_1}} \right| = 1,\left| {{z_2}} \right| = 3\) và \(\widehat {MON} = {120^o }\). Giá trị lớn nhất của \(\left| {3{z_1} + 2{z_2} - 3i} \right|\) là \({M_0}\), giá trị nhỏ nhất của \(\left| {3{{\rm{z}}_1} - 2{z_2} + 1 - 2i} \right|\) là \({m_0}\). Biết \({M_0} + {m_0} = a\sqrt 7 + b\sqrt 5 + c\sqrt 3 + d\), với \(a,b,c,d \in \mathbb{Z}.a + b + c + d = \) (1) ________
Cho M là điểm biểu diễn số phức z và N là điểm biểu diễn số phức \(w = - 4 - 3i\). Biết \(MN = 3\).

Độ dài đoạn thẳng ON bằng _____.
Tập hợp điểm biểu diễn số phức z là đường tròn có tọa độ tâm là (_____; _____) và bán kính bằng _____.
Chia ngẫu nhiên 20 hộp bánh giống nhau thành 4 phần quà (phần nào cũng có bánh). Có bao nhiêu cách chia để mỗi phần quà đều có ít nhất 3hộp bánh.
220.
495.
330.
165.
Cho ba số \(a = {1000^{1001}},b = {2^{{2^{64}}}}\) và \(c = {1^1} + {2^2} + {3^3} + \ldots + {1000^{1000}}\).
\(c < a < b\).
\(b < a < c\).
\(c < b < a\).
\(a < c < b\).
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 8 , mặt bên SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ \(B\) đến mặt phẳng \((SAC)\) là \(\frac{{a\sqrt b }}{c}\) (phân số tối giản với \(c > 0)\). Tính \(a + {b^2} - {c^3}\).
−485.
−214.
106.
203.
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau

Biết đồ thị hàm số \(y = \frac{{\sqrt {x + 3} + ax + b}}{{{{(x - 1)}^2}}}\,\,(C)\) không có tiệm cận đứng. Khi đó, a = _____ ; b = ____ và đồ thị hàm số có tiệm cận ngang là y = _____.
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau

Giá trị \(r\) của số phức zw bằng _____.
Giá trị \(\cos \varphi \) của số phức \(\frac{w}{z}\) bằng _____.
Giá trị \(n\) của số phức \({z^n}\) bằng _____.
Cho \(\log _2^2(xy) = {\log _2}\left( {\frac{x}{4}} \right){\log _2}(4y)\). Biểu thức \(P = {\log _3}(x + 4y + 4) + {\log _2}(x - 4y - 1)\) có giá trị bằng bao nhiêu?
3.
2.
\(\frac{5}{6}\).
\(\frac{3}{2}\).
Trong không gian Oxyz, cho mặt phẳng \((P)\) có phương trình \(2x + 2y - z + 1 = 0\) và đường thẳng \(d\) có phương trình \(\left\{ {\begin{array}{*{20}{c}}{x = 1 + t}\\{y = t}\\{z = - 2 - t}\end{array}} \right.\)
Gọi \(I\) là giao điểm của đường thẳng đi qua các điểm \(A(1;1;1),B(2; - 1; - 3)\) với mặt phẳng \((P)\).
Mỗi phát biểu sau đây là đúng hay sai?
Phát biểu | Đúng | Sai |
Điểm M(0;−1;−1) là giao điểm của d và (P). | ||
\(\frac{{AI}}{{BI}} = \frac{4}{3}\). | ||
Hình chiếu d′ của đường thẳng d trên mặt phẳng (P) có phương trình \(\frac{x}{{ - 2}} = \frac{{y + 1}}{{ - 2}} = \frac{{z + 1}}{1}\). |
Cho khai triển \({(1 + 2x)^n} = {a_0} + {a_1}x + {a_2}{x^2} + \ldots + {a_n}{x^n},n \ge 1\) thỏa mãn \({a_k} = {a_{k + 1}}\) (với \(k\) là số tự nhiên \((0 \le k \le n - 1)\) ).
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
Hệ số \(k = \frac{{an - 1}}{b}\) với ab bằng ______.
Số giá trị nguyên của \(n\) với \(n \le 2023\) thỏa mãn là ______.
Cho hàm số \(f(x) = \frac{{x - m}}{{x + 4}}\). Tổng tất cả các giá trị của \(m\) để \(\mathop {\min }\limits_{[ - 3;3]} f(x) = 2\) là
0.
−11.
−16.
1.
Giả sử \(f(x)\) là hàm số liên tục và luôn dương trên [0; 6] thỏa mãn \(\sqrt {f(x)f(6 - x)} = 1\) với mọi \(x \in [0;6]\). Giá trị của \(I = \int\limits_0^6 {\frac{{{\rm{d}}x}}{{1 + \sqrt {f(x)} }}} \) bằng (1) ________.
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại \(A\) và \(D\), \(AB = AD = 2a,CD = a\), góc giữa hai mặt phẳng \((SBC)\) và \((ABCD)\) bằng \({30^o }\). Gọi \(I\) là trung điểm của AD. Biết hai mặt phẳng \((SBI)\) và \((SCI)\) cùng vuông góc với mặt phẳng \((ABCD)\), khoảng cách giữa SA và CD là \(\frac{{a\sqrt k }}{2}\) với \(k = \) (1) _________.
Cho hàm số \(f(x)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \(f'(x) = {x^2}(x + 2)(x - 3)\).
Mỗi phát biểu sau đây là đúng hay sai?
Phát biểu | Đúng | Sai |
Hàm số \(f(x)\) có 3 điểm cực trị. | ||
Hàm số \(f(x)\) nghịch biến trên (-2;3). | ||
Hàm số \(f(x)\) có điểm cực đại là x = 2. |
Trong buổi sáng thứ sáu có 150 người đến phòng khám An Tâm kiểm tra sức khoẻ. Kết quả xét nghiệm nhóm máu của 150 người đó được thể hiện qua biểu đồ dưới đây.
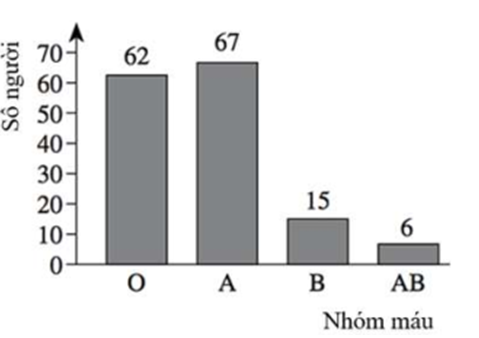
Chọn ngẫu nhiên một trong 150 người đã kiểm tra sức khoẻ. Xác suất để người này có nhóm máu A hoặc AB là
\(\frac{{73}}{{150}}\)
\(\frac{{61}}{{150}}\)
\(\frac{{68}}{{150}}\)
\(\frac{{82}}{{150}}\)
Điền số nguyên dương thích hợp vào những chỗ trống.
Trong không gian Oxyz, cho \(A(1;1;1)\) và \(B(1; - 2;4)\) và điểm \(M\) thoả mãn \(2\overrightarrow {MA} + \overrightarrow {MB} = \vec 0\). Hoành độ điểm \(M\) là (1) _____; tung độ điểm \(M\) là (2) ______; cao độ điểm \(M\) là (3) _____.
Cho hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{ - 2(x + 1){\rm{ khi}}\,\,x \le 0}\\{m\left( {1 - {x^2}} \right){\rm{ khi }}x > 0}\end{array}} \right.\). Để \(\int\limits_{ - 1}^1 {f(x){\rm{d}}x = 7} \) thì giá trị của m bằng bao nhiêu?
m = 12.
m = 9.
m = 6.
m = ∅.
Cho phương trình \(3{\cos ^2}x + 2|\sin x| = m\) (∗) với m là tham số.
Mỗi phát biểu sau đây là đúng hay sai?
Phát biểu | Đúng | Sai |
Với m = 1, phương trình (∗) có 4 điểm biểu diễn nghiệm trên đường tròn lượng giác. | ||
Có 2 giá trị nguyên của tham số m để phương trình (∗) có nghiệm. | ||
Có một giá trị của tham số m để phương trình (∗) có nghiệm duy nhất thuộc đoạn \(\left[ { - \frac{\pi }{4};\frac{\pi }{4}} \right]\). |
Tập hợp tất cả các giá trị thực của tham số m để bất phương trình \({\log _4}\left( {{x^2} - x - m} \right) \ge {\log _2}(x - 2)\) có nghiệm với mọi giá trị x thuộc tập xác định là
(−∞;−2).
[−2;+∞).
(−∞;2).
(−∞;2].
Cho cấp số cộng (un) có công sai d. Biết \[{u_2} + {u_{22}} = 40\]. Tính \({S_{23}}\).
690.
230.
920.
460.
Trong không gian Oxyz, cho 2 vectơ \(\vec a,\vec b\) tạo với nhau góc \({120^o }\) và \(|\vec a| = 3;|\vec b| = 5\). Giá trị của \(T = |\vec a - \vec b|\) bằng (1) _______.
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau
Khoảng cách từ tâm mặt cầu (S) đến đường thẳng d bằng _______.
Mặt phẳng (P) chứa đường thẳng d và có khoảng cách từ tâm mặt cầu (S) tới mặt phẳng là lớn nhất có phương trình \[ax + by + cz = 18\] với a = _______ ; b = _______; c = _______.
Khi thể tích của khối cầu giảm 8 lần thì diện tích của mặt cầu giảm
16.
8.
4.
2.
Bạn Xuân là thành viên trong một nhóm gồm 15 người.
Mỗi phát biểu sau đây là đúng hay sai?
Phát biểu | Đúng | Sai |
Chọn ngẫu nhiên 3 người từ nhóm để lập một ban đại diện. Xác suất để Xuân là 1 trong 3 người được chọn là 0,2. | ||
Chọn ngẫu nhiên 2 người từ nhóm để làm nhóm trưởng và nhóm phó. Xác suất để Xuân không làm nhóm trưởng cũng như nhóm phó nhỏ hơn 0,8. |
Cho 5 đoạn thẳng có độ dài là 1; 2; 3; 4; 5. Lấy ngẫu nhiên ba đoạn thẳng. Xác suất để độ dài ba đoạn thẳng này là độ dài ba cạnh của một tam giác là (1) _______.
Xét các số thực a, b thỏa mãn điều kiện \({\log _5}\left( {{5^a}{{.125}^b}} \right) = {\log _{25}}5\).
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau
Nếu \(b = \frac{1}{2}\) thì giá trị của số thực a bằng _______.
Mối liên hệ giữa a và b là \(2a + 6b = \) _______.
Nếu a là số nguyên âm thuộc [−10;−5] thì có _______ giá trị nguyên dương của b
Quan sát một nhóm học sinh chơi đá cầu, ta nhận thấy, khi quả cầu được đá lên, nó sẽ đạt một độ cao nhất định rồi rơi xuống đất. Biết rằng quỹ đạo của quả cầu là một cung parabol trong mặt phẳng với hệ tọa độ Oth, trong đó t là thời gian (tính bằng giây) kể từ khi quả cầu được đá lên, h là độ cao (tính bằng mét (m)). Giả sử quả cầu được đá từ độ cao 1 (m) và đạt được độ cao 6 (m) sau 1 giây, đồng thời sau 6 giây quả cầu lại trở về độ cao 1 (m). Độ cao lớn nhất mà quả cầu đạt được trong khoảng thời gian 5 giây kể từ lúc bắt đầu được đá là
6 (m)
7 (m)
10 (m)
13 (m)
Trong không gian Oxyz, cho mặt phẳng \((P):ax + by + cz + 3 = 0\) chứa hai điểm \(A( - 1;1;1)\), \(B(1;0;4)\) và vuông góc với mặt phẳng \((Q):3x + 2y + z = 0\). Giá trị của \(a + 2b - 3c\) bằng
−4.
0.
2.
4.
Cho số phức \(z\) thỏa mãn \(|z - 1 - 2i| \le 1\) và \(|z - 1 + 2i| \ge |z + 3 - 2i|\). Diện tích phần mặt phẳng chứa các điểm biểu diễn của số phức \(z\) bằng (1) _______. (Lấy \(\pi \approx 3,14\) và kết quả viết dưới dạng phân số tối giản).
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {(x - 2)^2} - 1\), trục hoành và hai đường thẳng \(x = 1,x = 2\).
\(\frac{1}{2}\).
2.
3.
\(\frac{2}{3}\).
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau![Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau Một chiếc ô tô đang đi trên đường với vận tốc \(v(t) = 3t - 15\,\,(t \ge 3)\,\,\left( {m/s} \right)\), trong đó t là khoảng thời gian tính bằng giây. Quãng đường ô tô đi được trong 10 giây bắt đầu từ thời điểm t = 3 là: ______(m). Khi ô tô đạt vận tốc 30 m/s thì người lái xe phát hiện có hàng rào chắn ngang đường ở phía trước cách xe 100 m (tính từ đầu xe tới hàng rào) nên người lái đạp phanh. Từ thời điểm đó, xe chuyển động chậm dần đều với vận tốc \[v\left( t \right) = - 5t + 100\,\,\left( {m/s} \right)\]. Từ lúc đạp phanh đến khi dừng hẳn ô tô còn di chuyển ______ (m). Khi xe dừng hẳn, khoảng cách từ xe đến hàng rào là ______ (m). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid16-1729673090.png)
Một chiếc ô tô đang đi trên đường với vận tốc \(v(t) = 3t - 15\,\,(t \ge 3)\,\,\left( {m/s} \right)\), trong đó t là khoảng thời gian tính bằng giây. Quãng đường ô tô đi được trong 10 giây bắt đầu từ thời điểm t = 3 là: ______(m).
Khi ô tô đạt vận tốc 30 m/s thì người lái xe phát hiện có hàng rào chắn ngang đường ở phía trước cách xe 100 m (tính từ đầu xe tới hàng rào) nên người lái đạp phanh. Từ thời điểm đó, xe chuyển động chậm dần đều với vận tốc \[v\left( t \right) = - 5t + 100\,\,\left( {m/s} \right)\]. Từ lúc đạp phanh đến khi dừng hẳn ô tô còn di chuyển ______ (m).
Khi xe dừng hẳn, khoảng cách từ xe đến hàng rào là ______ (m).
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = 3\sin x + 4\cos x + 1\) bằng (1) ______.
Định luật làm mát của Newton phát biểu rằng tốc độ làm mát của một vật tỉ lệ thuận với chênh lệch nhiệt độ giữa vật đó và môi trường xung quanh, với điều kiện là chênh lệch này không quá lớn. Giả sử T(t) là nhiệt độ của vật thể (đơn vị: độ C) tại thời điểm t (đơn vị: phút) và Ts là nhiệt độ của môi trường xung quanh, chênh lệch giữa nhiệt độ của vật thể và môi trường xung quanh là \(y(t) = T(t) - {T_s}\) thì \(\frac{{y'(t)}}{{y(t)}} = k\) với k là hằng số.
Một cốc nước đang ở nhiệt độ phòng là 22∘C được đưa vào ngăn mát tủ lạnh có nhiệt độ là 5∘C . Sau 30 phút, nhiệt độ của cốc nước được đo lại là 16∘C. Giả sử T (t) là nhiệt độ của cốc nước, y (t) là nhiệt độ chênh lệch giữa cốc nước và nhiệt độ ngăn mát tủ lạnh sau khoảng thời gian t.
Mỗi phát biểu sau đây là đúng hay sai?
Phát biểu | Đúng | Sai |
Nhiệt độ của chênh lệch giữa cốc nước và nhiệt độ ngăn mát tủ lạnh sau khoảng thời gian t là hàm số có dạng \(y(t) = y(0){e^{kt}}\). | ||
Kết quả làm tròn đến chữ số thập phân thứ tư của k là −0,0145. | ||
Sau 60 phút trong tủ lạnh, nhiệt độ của cốc nước khoảng 10∘C (Kết quả làm tròn đến chữ số hàng đơn vị). |
Cho hàm số \(f(x)\) liên tục trên \(\mathbb{R}\) thỏa mãn \(f(x) = 3f\left( {\frac{x}{2}} \right)\). Gọi \(F(x)\) là nguyên hàm của \(f(x)\) trên \(\mathbb{R}\) thỏa mãn \(F(4) = 1\) và \(2F(8) + 5F(2) = 0\).
Mỗi khẳng định sau đúng hay sai?
Phát biểu | Đúng | Sai |
1) \(F(x) = \frac{3}{2}F\left( {\frac{x}{2}} \right)\). | ||
2) \[F\left( 8 \right) < 0\]. | ||
3) \(\int\limits_0^2 {f(3x + 2)dx = 6} \). |
Cho khối nón (N) và khối trụ (T) có thể tích lần lượt là V1 và V2. Biết có chiều cao của hình nón (N) bằng một nửa chiều cao của hình trụ (T) và đường kính đáy của hình nón gấp đôi đường kính đáy của hình trụ. Tỉ lệ thể tích \(\frac{{{V_2}}}{{{V_1}}}\) bằng
\(\frac{3}{2}\).
\(\frac{4}{3}\).
\(\frac{3}{4}\).
\(\frac{2}{3}\).
Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (–50; 50) để bất phương trình \({\rm{m}} < \frac{{{5^{\rm{x}}} + {4^{\rm{x}}}}}{{{5^{\rm{x}}} - {4^{\rm{x}}}}}\) nghiệm đúng với mọi \[x \in \left( {\;0; + \infty } \right)\]?
51
50
49
48
Cho hàm số \(y = (m - 1){x^4} + \left( {{m^2} - 2} \right){x^2} + 2023\) (\(m\) là tham số).
Mỗi phát biểu sau là đúng hay sai?
Phát biểu | Đúng | Sai |
Đồ thị của hàm số đã cho luôn đi qua điểm (0;2023) với mọi \(m\). | ||
Với m = 1 thì hàm số đã cho có đúng 1 cực trị. | ||
Để hàm số đã cho đạt cực tiểu tại x = 1 thì \[m = {\rm{ }} - 1 - \sqrt 5 \]. |
Cho số phức \(z\) thoả mãn \(|z - 3 - 4i| = \sqrt 5 \). Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P = |z + 2{|^2} - |z - i{|^2}\). Tổng \(M + m\) bằng (1) _______.








