Đề thi ôn tốt nghiệp THPT Toán có lời giải ( Đề 4)

Giá trị lớn nhất của hàm số \(f\left( x \right) = {x^3} - 3{x^2} + 2\) trên đoạn \(\left[ { - 1;1} \right]\) bằng

Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho ứng với mỗi \(m\), hàm số \(y = \frac{1}{3}{x^3} + {x^2} - mx - 1\) có đúng một điểm cực trị thuộc khoảng \(\left( {0;4} \right)\)?

Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) thoả mãn \(f\left( { - 1} \right) = 1\) và \(f'\left( { - 1} \right) = - 4\). Phương trình tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm \(M\left( { - 1;1} \right)\) là:

Hàm số nào sau đây có đồ thị là đường cong như bên?

Trong không gian \(Oxyz\), mặt phẳng \(\left( P \right)\) đi qua điểm \(A\left( {1;0;2} \right)\) và vuông góc với đường thẳng \(d:\frac{x}{2} = \frac{{y - 1}}{{ - 1}} = \frac{{z + 2}}{3}\) có phương trình là

Câu lạc bộ cờ vua của trường Lê Lợi có 4 học sinh lớp 10; 6 học sinh lớp 11 và 5 học sinh lớp 12. Chọn ngẫu nhiên 3 học sinh từ câu lạc bộ. Xác suất để có ít nhất 2 học sinh khối 10 trong 3 học sinh được chọn là

Cho hàm số \(y' = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có một nguyên hàm là \(F\left( x \right).\) Biết rằng \(F\left( 1 \right) = 9{\kern 1pt} ,F\left( 2 \right) = 5.\) Giá trị của biểu thức \(\int\limits_1^2 {f\left( x \right)} \,{\rm{d}}x\) bằng:

Độ cao các bậc cầu thang so với mặt sàn tầng 1 của một căn nhà theo thứ tự lập thành một cấp số cộng với công sai \(d = 16\;{\rm{cm}}\), bậc thứ nhất có độ cao \({u_1} = 16\;{\rm{cm}}\). Bậc thứ năm có độ cao so với mặt sàn tầng 1 bằng

Nguyên hàm của hàm số \(f\left( x \right) = {5^{2x}}\) là

Cho hình phẳng \(\left( H \right)\) giới hạn bởi đồ thị hàm số \(y = f\left( x \right) = x - 2\), trục hoành và hai đường thẳng \(x = 3,x = 4\). Thể tích vật thể tròn xoay được tạo thành khi quay \(\left( H \right)\) quanh trục hoành là

Thời gian đọc sách mỗi ngày của một số học sinh được cho trong bảng sau.

Xác định trung vị của mẫu số liệu ghép nhóm.

Cho hàm số \(y = f\left( x \right) = - x + 1 - \frac{1}{{x - 1}}\).

a) Đường thẳng \(y = x - 1\) là tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right)\).

b) Đạo hàm của hàm số \(y = f\left( x \right)\) là \(f'\left( x \right) = \frac{{2x - {x^2}}}{{{{\left( {x - 1} \right)}^2}}},x \ne 1\).

c) Giá trị cực tiểu của hàm số \(y = f\left( x \right)\) là \( - 2\).

d) Bất phương trình \({x^2} + \left( {m - 2} \right)x - m + 2 \ge 0\) nghiệm đúng với mọi \(x > 1\) nếu \(m \ge - 2\).

Gọi \(D\) là hình phẳng giới hạn bởi các đồ thị hàm số \(y = \sqrt x ,y = \frac{1}{2}\sqrt x \) và hai đường thẳng \(x = 0,x = 4\).

a)Gọi \({V_1}\) là thể tích khối tròn xoay được tạo khi quay hình phẳng giới hạn bởi các đường \(y = 0,\)\(y = \sqrt x \), \(x = 0,x = 4\) quanh trục \(Ox\). Khi đó \({V_1} = \pi \int\limits_0^4 {x{\rm{d}}x} .\)

b)Gọi \({V_2}\) là thể tích khối tròn xoay được tạo khi quay hình phẳng giới hạn bởi các đường \(y = 0,\)\(y = \frac{1}{2}\sqrt x \), \(x = 0,x = 4\) quanh trục \(Ox\). Khi đó \({V_2} = \pi \int\limits_0^4 {\frac{1}{4}x{\rm{d}}x} .\)

c)Giá trị của biểu thức \({V_1} - {V_2}\) bằng \(12\pi \).

d)Một vật thể A có hình dạng được tạo thành khi quay hình phẳng \(D\)quanh trục \(Ox\)( đơn vị trên hai trục tính theo centimét). Thể tích của vật thể đó (làm tròn đến hàng phần mười theo đơn vị centimét khối) là \(37,7{\rm{c}}{{\rm{m}}^3}\).

Trong không gian \(Oxyz\), cho hình chóp đều \(S.ABCD\) có đáy \(ABCD\) là hình vuông tâm \(O\), cạnh bằng \(2\sqrt 2 \), cạnh bên \(SA = 4\) (tham khảo hình vẽ).

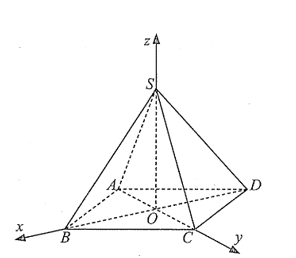
a) Tọa độ của điểm \(A\) là \(\left( {0;2;0} \right)\).

b) Trọng tâm của tam giác \(SAB\) là \(G\left( {\frac{2}{3}; - \frac{2}{3};\frac{{2\sqrt 3 }}{3}} \right)\).

c) Nếu \(E\left( {a;0;b} \right)\) là điểm trên mặt phẳng \(\left( {Oxz} \right)\) sao cho ba điểm \(C,E,G\) thẳng hàng thì \(a \cdot b = \sqrt 3 \).

d) Nếu \(M\left( {0;m;n} \right)\) là điểm trên mặt phẳng \(\left( {Oyz} \right)\) sao cho \(MG + MB\) đạt giá trị nhỏ nhất thì \({m^2} + {n^2} = 1\).

Một xí nghiệp mỗi ngày sản xuất ra \(2000\) sản phẩm trong đó có \(39\) sản phẩm lỗi. Lần lượt lấy ra ngẫu nhiên hai sản phẩm không hoàn lại để kiểm tra. Tính xác suất của biến cố: Sản phẩm lấy ra lần thứ hai bị lỗi (làm tròn kết quả đến hàng phần trăm).

Tại một nhà máy, khi sản xuất \(x\) tạ sản phẩm \(\left( {x > 0} \right)\) mỗi ngày thì chi phí trung bình trên mỗi tạ sản phẩm được tính bởi công thức \(\overline C \left( x \right) = \frac{1}{2}x + 3 + \frac{8}{x}\) (triệu đồng/tạ). Tính chi phí trung bình thấp nhất (tính theo triệu đồng/tạ) mà nhà máy có thể đạt được trong ngày.

Trong không gian \(Oxyz\), cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\left( {0;0;0} \right),B\left( {6;0;0} \right)\) và cạnh bên \(SA\) vuông góc với mặt phẳng đáy. Biết rằng \(D\left( {0;x;0} \right)\) với \(x > 0\) thỏa mãn \(AD = 2AB = 2BC\), góc giữa đường thẳng \(SC\)và mặt phẳng đáy bằng \(45^\circ \). Tính khoảng cách từ \(B\) đến mặt phẳng \(\left( {SCD} \right)\).

Trong điều kiện nuôi cấy thích hợp, cứ 20 phút vi khuẩn E. Coli lại phân đôi một lần. Giả sử lúc đầu có 5 vi khuẩn và sau \(n\) phút (\(n \in \mathbb{N}\)) có hơn 2000 vi khuẩn. Giá trị nhỏ nhất của \(n\) là bao nhiêu?

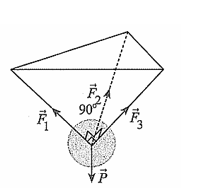
Treo một vật nặng có trọng lượng 30 N bởi ba sợi dây giống hệt nhau, các sợi dây đôi một tạo với nhau một góc \(90^\circ \)như hình vẽ. Gọi \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) lần lượt là các lực căng của ba sợi dây nói trên. Độ lớn của lực \(\overrightarrow {{F_1}} \) bằng bao nhiêu Newton (làm tròn kết quả đến hàng phần trăm)?