Đề thi ôn tốt nghiệp THPT Toán có lời giải ( Đề 1)
22 câu hỏi
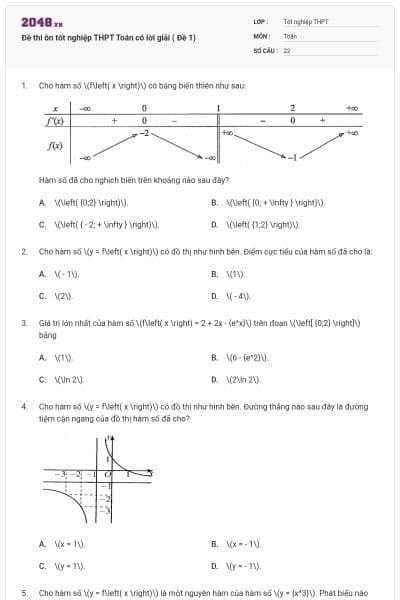
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:

Hàm số đã cho nghịch biến trên khoảng nào sau đây?
\(\left( {0;2} \right)\).
\(\left( {0; + \infty } \right)\).
\(\left( { - 2; + \infty } \right)\).
\(\left( {1;2} \right)\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên. Điểm cực tiểu của hàm số đã cho là:
\( - 1\).
\(1\).
\(2\).
\( - 4\).
Giá trị lớn nhất của hàm số \(f\left( x \right) = 2 + 2x - {e^x}\) trên đoạn \(\left[ {0;2} \right]\) bằng
\(1\).
\(6 - {e^2}\).
\(\ln 2\).
\(2\ln 2\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên. Đường thẳng nào sau đây là đường tiệm cận ngang của đồ thị hàm số đã cho?
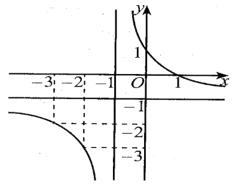
\(x = 1\).
\(x = - 1\).
\(y = 1\).
\(y = - 1\).
Cho hàm số \(y = f\left( x \right)\) là một nguyên hàm của hàm số \(y = {x^3}\). Phát biểu nào sau đây đúng?
\(f\left( x \right) = \frac{{{x^4}}}{4} + C\).
\(f\left( x \right) = 3{x^2}\).
\(f\left( x \right) = 4{x^3}\).
\(f\left( x \right) = \frac{{{x^4}}}{4}\).
Nếu hàm số \(f\left( x \right)\) thỏa mãn \(\int\limits_1^3 {f\left( x \right){\rm{d}}x} = 6\) và \(\int\limits_1^5 {f\left( x \right){\rm{d}}x = 20} \) thì giá trị của \(\int\limits_3^5 {f\left( x \right){\rm{d}}x} \) bằng
\( - 14\).
\(26\).
\(14\).
\(28\).
Một hộp chứa 4 viên bi xanh, 3 viên bi đỏ và 1 viên bi vàng. Các viên bi có cùng kích thước và khối lượng. Bạn Hà lấy ra ngẫu nhiên 1 viên bi từ hộp. Xác suất viên bi lấy ra không có màu vàng, biết rằng nó không có màu đỏ là
\(\frac{1}{2}\).
\(\frac{5}{8}\).
\(\frac{7}{8}\).
\(\frac{4}{5}\).
Xét mẫu số liệu ghép nhóm có tứ phân vị thứ nhất, tứ phân vị thứ hai, tứ phân vị thứ ba lần lượt là \({Q_1};{Q_2};{Q_3}\). Khoảng tứ phân vị của mẫu số liệu ghép nhóm đó bằng
\({Q_2} - {Q_1}\).
\({Q_3} - {Q_2}\).
\({Q_3} - {Q_1}\).
\({Q_3} - 2{Q_2} + {Q_1}\).
Số nghiệm của phương trình \(\sin 2x + \cos x = 0\) trên \(\left[ {0;2\pi } \right]\) là
\(3\).
\(1\).
\(2\).
\(4\).
Chỉ số hay độ \(pH\) của một dung dịch được tính theo công thức \(pH = - \log \left[ {{H^ + }} \right]\) với \(\left[ {{H^ + }} \right]\) là nồng độ ion hydrogen. Độ \(pH\) của một loại sữa có \(\left[ {{H^ + }} \right] = {10^{ - 6,8}}\) là bao nhiêu?
\( - 6,8\).
\(68\).
\(6,8\).
\(0,68\).
Trong không gian \(Oxyz\), cho điểm \(A\left( {1;2; - 1} \right)\) và mặt phẳng \(\left( P \right):x + 2y + z = 0\). Mặt phẳng \(\left( Q \right)\) qua \(A\) và song song với mặt phẳng \(\left( P \right)\) có phương trình là
\(x + 2y + z - 1 = 0\).
\(x + 2y + z + 4 = 0\).
\(x + 2y + z - 6 = 0\).
\(x + 2y + z - 4 = 0\).
Trong không gian \(Oxyz\), cho điểm \(I\left( {0; - 3;1} \right)\) và \(R = 2\). Mặt cầu tâm \(I\), bán kính \(R\) có phương trình là
\({x^2} + {\left( {y + 3} \right)^2} + {\left( {z - 1} \right)^2} = 4\).
\({x^2} + {\left( {y - 3} \right)^2} + {\left( {z + 1} \right)^2} = 4\).
\({x^2} + {\left( {y + 3} \right)^2} + {\left( {z - 1} \right)^2} = 2\).
\({x^2} + {\left( {y - 3} \right)^2} + {\left( {z + 1} \right)^2} = 2\).
Nồng độ thuốc \(C\left( t \right)\) tính theo mg/cm3 trong máu của bệnh nhân được tính bởi \(C\left( t \right) = \frac{{0,05t}}{{{t^2} + t + 1}}\), trong đó \(t\) là thời gian tính theo giờ kể từ khi tiêm cho bệnh nhân.
a) Hàm số \(C\left( t \right)\) có đạo hàm \(C'\left( t \right) = \frac{{1 - {t^2}}}{{20{{\left( {{t^2} + t + 1} \right)}^2}}},t \ge 0\).
b) Sau khi tiêm, nồng độ thuốc trong máu của bệnh nhân giảm dần theo thời gian.
c) Nồng độ thuốc trong máu lớn nhất ở thời điểm 1 giờ sau khi tiêm.
d) Có thời điểm nồng độ trong máu của bệnh nhân đạt 0,02 mg/cm3.
Cho hai hàm số \(f\left( x \right) = {e^x}\) và \(g\left( x \right) = 2{e^x} - 3\).
a) \(\int\limits_0^{\ln 2} {g\left( x \right){\rm{d}}x = 2 - 3\ln 2} \).
b) \(2\int\limits_0^2 {f\left( x \right){\rm{d}}x} = 3 + \int\limits_0^2 {g\left( x \right){\rm{d}}x} \).
c) \(\int\limits_2^7 {\left[ {2f\left( x \right) - g\left( x \right)} \right]} \,{\rm{d}}x = - 15\).
d) Nếu \(\int\limits_0^1 {f\left( x \right)g\left( x \right){\rm{d}}x} = a \cdot {e^2} + b \cdot e + c\) (với \(a,b,c\) là các số nguyên) thì \(a + b + c = 0\).
Trong không gian \(Oxyz\), cho tứ diện \(ABCD\) có \(A\left( {1;0;0} \right)\), \(B\left( {0;1;0} \right)\), \(C\left( {0;0;1} \right)\), \(D\left( { - 2;1; - 1} \right)\).
a) Phương trình tổng quát của mặt phẳng \(\left( {BCD} \right)\) là \(x - 2y - 2z + 2 = 0\).
b) Điểm \(B\) thuộc mặt phẳng \(\left( {ACD} \right)\).
c) Độ dài đường cao của hình chóp \(A.BCD\) bằng 3.
d) Mặt phẳng đi qua điểm \(A\) và vuông góc với hai mặt phẳng \(\left( {ACD} \right),\left( {BCD} \right)\) có phương trình tổng quát là \(x - y + 2z + 1 = 0\).
Kết quả kiểm tra cân nặng của 20 học sinh nam lớp 12A (làm tròn kết quả đến hàng đơn vị của kilôgam) được cho bởi bảng sau:
Nhóm | Giá trị đại diện | Tần số |
\[\left[ {60;64} \right)\] | 62 | 9 |
\[\left[ {64;68} \right)\] | 66 | 8 |
\[\left[ {68;72} \right)\] | 70 | 1 |
\[\left[ {72;76} \right)\] | 74 | 1 |
\[\left[ {76;80} \right)\] | 78 | 1 |
|
| \(n = 20\) |
a) Khoảng biến thiên của mẫu số liệu ghép nhóm đã cho là 20.
b) Số trung bình cộng của mẫu số liệu ghép nhóm đã cho được tính bằng công thức
\(\overline x = \frac{{8 \cdot 62 + 9 \cdot 66 + 1 \cdot 70 + 1 \cdot 74 + 1 \cdot 78}}{{20}}\).
c) Phương sai của mẫu số liệu ghép nhóm đã cho là \({s^2} = \sqrt {\frac{{436}}{{25}}} \).
d) Độ lệch chuẩn của mẫu số liệu ghép nhóm đã cho (làm tròn kết quả đến hàng phần mười của kilôgam) là 4 kg.
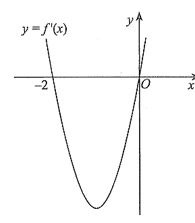
Đạo hàm \(f'\left( x \right)\) của hàm số \(f\left( x \right)\) là một hàm số bậc hai và hàm số \(y = f'\left( x \right)\) có đồ thị như hình bên. Biết rằng hàm số \(f\left( x \right)\) có giá trị cực đại là 2 và giá trị cực tiểu là \( - 2\). Tìm giá trị của \(f\left( 2 \right)\).
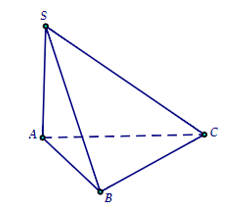
Cho hình chóp \(S.ABC\) có đáy là tam giác đều cạnh \(2\), \(SA\) vuông góc với đáy. Biết góc giữa mặt phẳng \(\left( {SBC} \right)\) và mặt đáy \(\left( {ABC} \right)\) bằng \(60^\circ \) (tham khảo hình vẽ bên). Tính thể tích khối chóp \(S.ABC\) (làm tròn kết quả đến hàng phần trăm).
Khi sử dụng phần mềm mô phỏng để thiết kế một chậu cây, người ta quay hình phẳng giới hạn bởi đồ thị hàm số \(y = \sqrt x + 2\), trục hoành và hai đường thẳng \(x = 0,x = 4\) quanh trục hoành. Biết đơn vị trên các trục tọa độ là decimét. Thể tích của chậu cây (làm tròn kết quả đến hàng phần mười) bằng bao nhiêu decimét khối?
Trong không gian \(Oxyz\), cho hai điểm \(A\left( {2; - 1; - 5} \right)\), \(B\left( { - 4;2;1} \right)\). Xét \(M\) là điểm thay đổi thỏa mãn điều kiện \(\left| {\overrightarrow {MA} + 2\overrightarrow {MB} } \right| = 9\). Độ dài đoạn thẳng \(OM\) lớn nhất bằng bao nhiêu (làm tròn kết quả đến hàng phần trăm).
Cho một tấm nhôm hình vuông cạnh \[12\,{\rm{cm}}\], người ta cắt ở bốn góc bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng \[x{\rm{ (cm)}}\], rồi gập tấm nhôm lại như bên dưới để được một cái hộp có dạng hình hộp chữ nhật không có nắp như hình dưới. Giá trị của \[x\] bằng bao nhiêu centimét để thể tích của khối hộp đó là lớn nhất (làm tròn kết quả đến hàng đơn vị)?
![Cho một tấm nhôm hình vuông cạnh \[12\,{\rm{cm}}\], người ta cắt ở bốn góc bốn hình vuông bằng nhau (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid8-1737208747.png)
Trong không gian với một hệ trục tọa độ cho trước (đơn vị đo lấy theo kilômét), một chiếc máy bay đang di chuyển với hướng bay không đổi từ điểm \(\left( { - 50;30;10} \right)\) đến vị trí hạ cánh là \(\left( {2;3;0} \right)\). Hỏi đường bay của máy bay hợp với mặt đất một góc bao nhiêu độ (làm tròn kết quả đến hàng phần trăm)?