Đề thi ôn tốt nghiệp THPT Toán có lời giải ( Đề 2)
22 câu hỏi
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
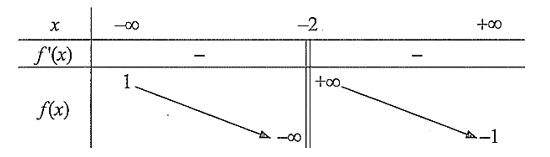
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
\(1\).
\(2\).
\(3\).
\(4\).
Cho hàm số \(y = {e^x}\left( {x - 2} \right)\). Hàm số nghịch biến trên khoảng nào sau đây?
\(\left( {2; + \infty } \right)\).
\(\left( {1; + \infty } \right)\).
\(\left( { - \infty ;2} \right)\).
\(\left( { - \infty ;1} \right)\).
Gọi \(M,m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(f\left( x \right) = x + 1 - \frac{4}{{x - 3}}\) trên đoạn \(\left[ { - 1;2} \right]\). Giá trị của \(M - m\) bằng
\(1\).
\(\frac{9}{5}\).
\(6\).
\(8\).
Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = \frac{{2x + 1}}{{x - m}}\) đồng biến trên khoảng \(\left( { - \infty ; - 4} \right)\)?
\(3\).
\(4\).
\(5\).
Vô số.
Hàm số nào sau đây là một nguyên hàm của hàm số \(f\left( x \right) = \sin x\)?
\({F_1}\left( x \right) = \sin x\).
\({F_2}\left( x \right) = - \sin x\).
\({F_3}\left( x \right) = \cos x\).
\({F_4}\left( x \right) = - \cos x\).
Biết rằng \(\int\limits_0^1 {\frac{{2{e^{2x}} + 3}}{{{e^x}}}} \,{\rm{d}}x = \frac{{m \cdot {e^2} + n \cdot e + p}}{e}\) (với \(m,n,p \in \mathbb{Z}\)). Khi đó \(m + 2n - p\) bằng
\(2\).
\(6\).
\(1\).
\(7\).
Cho \(A\) và \(B\) là hai biến cố độc lập thoả mãn \(P\left( A \right) = 0,5\) và \(P\left( B \right) = 0,3\). Khi đó, \(P\left( {A \cap B} \right)\) bằng:
\(0,8\).
\(0,2\).
\(0,6\).
\(0,15\).
Bảng sau ghi lại điểm tổng kết cuối năm môn Ngữ văn của các học sinh lớp 12D.
Điểm | \[\left[ {7;\,7,5} \right)\] | \[\left[ {7,5;\,8} \right)\] | \[\left[ {8;\,8,5} \right)\] | \[\left[ {8,5;\,9} \right)\] |
Số học sinh | 6 | 16 | 13 | 5 |
Phương sai của mẫu số liệu trên thuộc khoảng
\(\left[ {0;0,2} \right)\).
\(\left[ {2,0;2,2} \right)\).
\(\left[ {3,3;3,5} \right)\).
\(\left[ {3,5;3,7} \right)\).
Cho tứ diện \(ABCD\). Gọi \(M,N\) lần lượt là trung điểm của \(BC,CD\) và \(G\) là trọng tâm của tam giác \(BCD\). Phát biểu nào sau đây sai?
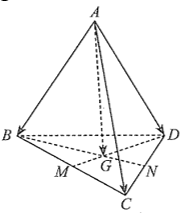
\(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AG} \).
\(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \).
\(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AN} = 3\overrightarrow {AG} \).
\(\overrightarrow {AC} + \overrightarrow {AD} = 2\overrightarrow {AN} \).
Trong không gian \(Oxyz\), cho mặt cầu tâm \(I\left( { - 2;1;5} \right)\), bán kính bằng \(3\). Điểm nào dưới đây thuộc mặt cầu đã cho?
\(C\left( {0;3;4} \right)\).
\(A\left( {10;1;2} \right)\).
\(B\left( {0;1;4} \right)\).
\(D\left( {0;2;1} \right)\).
Trong không gian \(Oxyz\), góc giữa hai đường thẳng \({d_1}:\left\{ \begin{array}{l}x = 1 + 2t\\y = 2 + t\\z = - 1 + t\end{array} \right.\) và \({d_2}:\left\{ \begin{array}{l}x = 3 - t\\y = 1 - 2t\\z = 5 + t\end{array} \right.\) bằng
\(60^\circ \).
\(120^\circ \).
\(30^\circ \).
\(90^\circ \).
Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_2} = - 6\) và \({u_6} = - 486\). Tìm công bội \(q\) của cấp số nhân đã cho, biết rằng \({u_3} > 0\).
\(q = - 3\).
\(q = - \frac{1}{3}\).
\(q = \frac{1}{3}\).
\(q = 3\).
Biết rằng hàm số \(f\left( x \right) = 2{x^3} + a{x^2} - 6x + b\)(\(a\) và \(b\) là hằng số thực) đạt cực trị bằng 4 tại \(x = 1\).
a) Giá trị của \(a + b\) bằng 8.
b) Hàm số đạt cực đại tại \(x = 1\).
c) \(x = - 1\) là một điểm cực trị của hàm số \(f\left( x \right)\).
d) Giá trị cực tiểu của hàm số \(f\left( x \right)\) bằng 12.
Trong không gian \(Oxyz\), cho điểm \(M\left( {3;1;9} \right)\), đường thẳng \(d:\left\{ \begin{array}{l}x = t\\y = - 1 - t\\z = 2 + 2t\end{array} \right.\) và mặt phẳng \(\left( \alpha \right):x + y - z + 3 = 0\).
a) Một vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\) là \(\overrightarrow n = \left( {1;1; - 1} \right)\).
b) Điểm \(M\) thuộc đường thẳng \(d\).
c) Một điểm \(A\) bất kì thuộc đường thẳng \(d\) đều có tọa độ dạng \(A\left( {t; - 1 - t;2 + 2t} \right)\).
d) Đường thẳng \(\Delta \) đi qua điểm \(M\), cắt đường thẳng \(d\) và song song với mặt phẳng \(\left( \alpha \right)\) có phương trình \(\frac{{x - 1}}{2} = \frac{{y + 2}}{3} = \frac{{z - 4}}{5}\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị là đường cong trong hình dưới đây. Gọi \(\left( H \right)\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và các đường thẳng \(x = - 1,x = 4\). Khi đó:
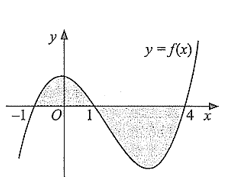
a) Diện tích \(S\) của hình phẳng \(\left( H \right)\) là \(S = \int\limits_{ - 1}^4 {\left| {f\left( x \right)} \right|{\rm{d}}x} \).
b) Diện tích \(S\) của hình phẳng \(\left( H \right)\) là \(S = \int\limits_{ - 1}^1 {f\left( x \right){\rm{d}}x} + \int\limits_1^4 {f\left( x \right){\rm{d}}x} \).
c) Nếu \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\) thì \(F\left( 1 \right) > F\left( { - 1} \right) > F\left( 4 \right)\).
d) Thể tích vật thể được tạo thành khi quay \(\left( H \right)\) quanh trục hoành là \(V = \int\limits_{ - 1}^4 {{{\left[ {f\left( x \right)} \right]}^2}{\rm{d}}x} \).
Khi kiểm tra sức khoẻ tổng quát của bệnh nhân ở một bệnh viện, người ta được kết quả như sau:
– Có \(40\% \) bệnh nhân bị đau dạ dày.
– Có \(30\% \) bệnh nhân thường xuyên bị stress.
– Trong số các bệnh nhân bị stress có \(80\% \) bệnh nhân bị đau dạ dày.
Chọn ngẫu nhiên 1 bệnh nhân.
a) Xác suất chọn được bệnh nhân thường xuyên bị stress là \(0,3\).
b) Xác suất chọn được bệnh nhân bị đau dạ dày, biết bệnh nhân đó thường xuyên bị stress, là \(0,8.\)
c) Xác suất chọn được bệnh nhân vừa thường xuyên bị stress vừa bị đau dạ dày là \(0,24.\)
d) Xác suất chọn được bệnh nhân thường xuyên bị stress, biết bệnh nhân đó bị đau dạ dày, là \(0,6.\)
Anh Hưng gửi tiết kiệm khoản tiền 700 triệu đồng vào một ngân hàng với lãi suất 7%/năm theo hình thức lãi kép kì hạn 12 tháng. Tính thời gian tối thiểu gửi tiết kiệm để anh Hưng thu được ít nhất 1 tỉ đồng (cả vốn lẫn lãi). Cho biết công thức lãi kép là \(T = A \cdot {\left( {1 + r} \right)^n}\), trong đó \(A\) là tiền vốn, \(T\) là tiền vốn và lãi nhận được sau \(n\) năm, \(r\) là lãi suất/năm.
Một thùng dầu bị rò rỉ từ lúc 13 giờ với tốc độ rò rỉ là \(v\left( t \right) = 16 + 3t\) (lít/giờ), trong đó \(t\) (giờ) là thời gian tính từ khi bắt đầu bị rò rỉ. Khi đó \(V\left( t \right)\) (lít) là thể tích dầu bị mất đi thỏa mãn \(V'\left( t \right) = v\left( t \right)\). Giả sử \({V_1}\) là thể tích dầu bị mất đi trong khoảng thời gian từ 13 giờ đến 16 giờ và \({V_2}\) là thể tích dầu bị mất đi trong khoảng thời gian từ 16 giờ đến 19 giờ. Tính \({V_2} - {V_1}\) (theo đơn vị lít).
Một xe ô tô chở khách du lịch có sức chứa tối đa là \[16\] hành khách. Trong một khu du lịch, một đoàn khách gồm \[22\] người đang đi bộ và muốn thuê xe về khách sạn. Lái xe đưa ra thỏa thuận với đoàn khách du lịch như sau: Nếu một chuyến xe chở \(x\) (người) thì giá tiền cho mỗi người là \(\frac{{{{\left( {40 - x} \right)}^2}}}{2}\) (nghìn đồng). Với thoả thuận như trên thì lái xe có thể thu được nhiều nhất bao nhiêu triệu đồng từ một chuyến chở khách (làm tròn kết quả đến hàng phần trăm)?
Bảng dưới đây thống kê nhiệt độ không khí trung bình của các tháng trong năm tại một trạm đo đạc (đơn vị: \(^\circ {\rm{C}}\)).
Nhiệt độ (\(^\circ {\rm{C}}\)) | \[\left[ {10;\,15} \right)\] | \[\left[ {15;\,20} \right)\] | \[\left[ {20;\,25} \right)\] | \[\left[ {25;\,30} \right)\] |
Số tháng | 3 | 4 | 4 | 1 |
Tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.
Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right)\): \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 6\) và hai mặt phẳng \(\left( P \right):x + y + 2z + 5 = 0\), \(\left( Q \right):2x - y + z - 5 = 0\). Hai đường thẳng \(d\) và \(\Delta \) đi qua tâm của \(\left( S \right)\), lần lượt vuông góc và cắt \(\left( P \right),\left( Q \right)\) theo thứ tự đó tại \(A\) và \(B\). Tính độ dài đoạn thẳng \(AB\) (làm tròn kết quả đến hàng phần trăm).
Một khối Rubik 4 × 4 được gắn với hệ tọa độ \[Oxyz\] có đơn vị trên mỗi trục bằng độ dài cạnh hình lập phương nhỏ (tham khảo hình vẽ bên). Xét mặt phẳng \[\left( P \right)\] đi qua 3 điểm \[A\left( {0;3;4} \right),B\left( {2;1;4} \right),C\left( {1;0;0} \right)\]. Góc giữa hai mặt phẳng \[\left( P \right)\] và \[\left( {Oxy} \right)\] bằng bao nhiêu độ (làm tròn kết quả đến hàng đơn vị)?