Đề thi ôn tốt nghiệp THPT Toán có lời giải ( Đề 3)
20 câu hỏi
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
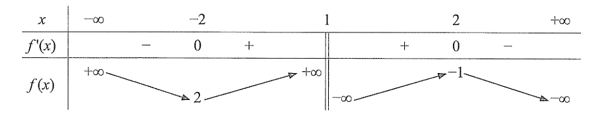
Số nghiệm của phương trình \(2f\left( x \right) - 3 = 0\) là
\(0\).
\(1\).
\(2\).
\(3\).
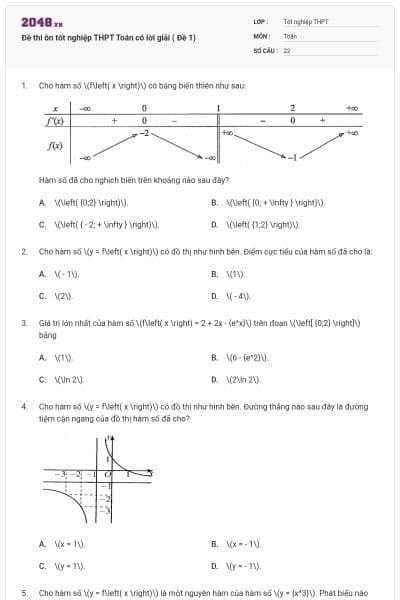
Hàm số nào dưới đây có đồ thị như hình vẽ.

\(y = \sin x\).
\(y = \cos x\).
\(y = \tan x\).
\(y = \cot x\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?
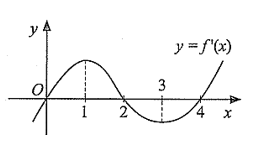
Hàm số \(y = f\left( x \right)\) đồng biến trên \(\left( { - \infty ;1} \right)\).
Hàm số \(y = f\left( x \right)\) nghịch biến trên \(\left( {2;4} \right)\).
Hàm số \(y = f\left( x \right)\) đạt cực tiểu tại \(x = 3\).
Hàm số \(y = f\left( x \right)\) đạt cực đại tại \(x = 4\).
Cho hàm số \(y = \frac{{a{x^2} + bx + c}}{{mx + n}},\left( {am \ne 0} \right)\) có đồ thị như hình vẽ bên. Phương trình đường tiệm cận xiên của đồ thị hàm số đã cho là:
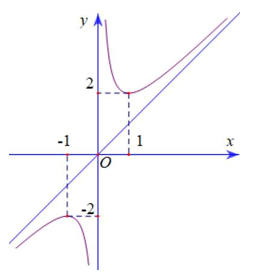
\(y = 2x\).
\(y = - x\).
\(y = x\).
\(y = - 2x\).
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}3{x^2} + 2\;{\rm{khi}}\;x \le 1\\8x - 3\;{\rm{khi}}\;x > 1\end{array} \right.\). Khi đó giá trị của \(\int\limits_{ - 2}^2 {f\left( x \right){\rm{d}}x} \) bằng
\(0\).
\(24\).
\( - 12\).
\( - 6\).
Trong không gian toạ độ \[Oxyz\], vectơ nào sau đây là vectơ chỉ phương của đường thẳng \(\Delta :\left\{ {\begin{array}{*{20}{l}}{x = - 4 + 2t}\\{y = 7 - 3t}\\{z = 8 - 9t}\end{array}} \right.\)?
\[{\vec u_1} = \left( {4\,;7\,;\,8} \right)\].
\[{\vec u_1} = \left( { - 4\,;7\,;8} \right)\].
\[{\vec u_3} = \left( {2\,;3\,;9} \right)\].
\[{\vec u_4} = \left( {2\,; - 3\,; - 9} \right)\].
Gieo hai con xúc xắc cân đối, đồng chất. Tính xác suất để tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn 10 hoặc bằng 10, biết rằng có ít nhất một con đã ra mặt 5 chấm.
\(\frac{6}{{11}}\).
\(\frac{4}{{11}}\).
\(\frac{5}{{11}}\).
\(\frac{3}{{11}}\).
Tập nghiệm \(S\) của bất phương trình \({5^{x + 2}} < {\left( {\frac{1}{{25}}} \right)^{ - x}}\) là
\(S = \left( { - \infty ;2} \right)\).
\(S = \left( { - \infty ;1} \right)\).
\(S = \left( {1; + \infty } \right)\).
\(S = \left( {2; + \infty } \right)\).
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành, cạnh bên \(SA\) vuông góc với đáy. Biết khoảng cách từ \(A\) đến \(\left( {SBD} \right)\) bằng \(\frac{{6a}}{7}\). Tính khoảng cách từ \(C\) đến mặt phẳng \(\left( {SBD} \right)\).
\(\frac{{12a}}{7}\).
\(\frac{{3a}}{7}\).
\(\frac{{4a}}{7}\).
\(\frac{{6a}}{7}\).
Một mẫu số liệu ghép nhóm về chiều cao của một lớp (đơn vị là centimét) có phương sai là \(6,25\). Độ lệch chuẩn của mẫu số liệu đó bằng:
\(2,5\;{\rm{cm}}\).
\(12,5\;{\rm{cm}}\).
\(3,125\;{\rm{cm}}\).
\(42,25\;{\rm{cm}}\).
Trong không gian với hệ tọa độ \(Oxyz,\) khoảng cách từ điểm \(I\left( {1;1;1} \right)\) đến mặt phẳng \(\left( P \right):2x - y + z - 16 = 0\) bằng?
\( - 6\).
\(18\).
\(\frac{{7\sqrt 6 }}{3}\).
\( - 18\).
Trong không gian với hệ tọa độ\(Oxyz\), cho mặt cầu có phương trình \({x^2} + {y^2} + {z^2} - 2x + 4y - 6z - 11 = 0\). Tọa độ tâm \(I\) và bán kính \(R\) của mặt cầu đã cho lần lượt là
\(I\left( {1; - 2;3} \right),R = 5\).
\(I\left( {1;2; - 3} \right),R = 5\).
\(I\left( { - 1; - 2;3} \right),R = 5\).
\(I\left( {1; - 2; - 3} \right),R = 5\).
Cần rào ba cạnh để cùng với bờ tường có sẵn tạo thành mảnh vườn hình chữ nhật có diện tích 200 m2 (tham khảo hình vẽ). Kí hiệu \(x\;\left( {\rm{m}} \right)\), \[y\;\left( {\rm{m}} \right)\] lần lượt là độ dài các cạnh của mảnh vườn vuông góc và song song với bờ tường; \(L\;\left( {\rm{m}} \right)\) là tổng độ dài lưới thép cần để rào mảnh vườn. Biết rằng mỗi mét lưới thép dùng để rào mảnh vườn có đơn giá 250 nghìn đồng.
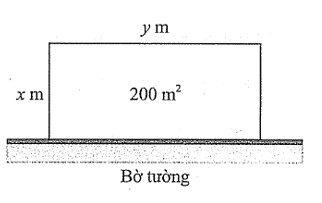
a)\(y\) được tính theo \(x\) bằng công thức \(y = \frac{{200}}{x}\).
b) \(L\) được tính theo \(x\) theo công thức \(L = 2x + \frac{{100}}{x}\).
c) \(L\) đạt giá trị nhỏ nhất khi \(x = 10\;\left( {\rm{m}} \right)\).
d) Số tiền tối thiểu để mua lưới thép rào mảnh vườn là 2,5 triệu đồng.
Một ô tô đang chạy đều với vận tốc \(x\left( {{\rm{m/s}}} \right)\) thì người lái xe đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc thay đổi theo hàm số \(v = - 5t + 20\left( {{\rm{m/s}}} \right)\), trong đó \(t\) là thời gian tính bằng giây kể từ lúc đạp phanh.
a) Khi xe dừng hẳn thì vận tốc bằng \(0\left( {{\rm{m/s}}} \right)\).
b) Thời gian từ lúc người lái xe đạp phanh cho đến khi xe dừng hẳn là \(5\,{\rm{s}}\).
c) \(\int {\left( { - 5t + 20} \right){\rm{dt}} = } \frac{{ - 5{t^2}}}{2} + 20t + C\).
d) Quãng đường từ lúc đạp phanh cho đến khi xe dừng hẳn là \(400\,{\rm{m}}\).
Trong không gian \(Oxyz\), cho các điểm \(A\left( {1; - 3;2} \right),B\left( {2;4; - 2} \right)\) và \(C'\left( {3;2; - 2} \right)\).
a) Trung điểm của đoạn thẳng \(OB\) là \(C\left( {1;2; - 1} \right)\).
b) Biết rằng tứ giác \(ACC'A'\) là hình bình hành. Cao độ của điểm \(A'\) là \(z = 1\).
c) Biết rằng điểm \(B'\) là đỉnh còn lại của lăng trụ \(ABC.A'B'C'\). Khi đó tung độ của điểm \(B'\) là \(y = - 3\).
d) Thể tích của khối lăng trụ \(ABC.A'B'C'\) bằng \(\frac{7}{2}\).
Bạn Ninh có 4 tấm thẻ được đánh số lần lượt là 3; 6; 8; 9. Ninh lấy ra 2 tấm thẻ trong 4 tấm thẻ đó và xếp chúng thành một hàng ngang một cách ngẫu nhiên để tạo thành một số có hai chữ số. Gọi \(A\) là biến cố “Số tạo thành chia hết cho 2” và \(B\) là biến cố “Số tạo thành chia hết cho 3”.
a) Xác suất của biến cố \(A\) là \(0,5\).
b) Xác suất của biến cố \(AB\) là \(0,25\).
c) Xác suất của biến cố \(A\) với điều kiện \(B\) là \(\frac{1}{3}\).
d) Xác suất của biến cố \(A\) với điều kiện \(\overline B \) là \(\frac{2}{3}\).
Ta coi năm lấy làm mốc để tính dân số của một vùng ( hoặc một quốc gia) là năm \(0\). Khi đó, dân số của quốc gia đó ở năm thứ \(t\) là hàm theo biến \(t\) được cho bởi công thức: \(S = A \cdot {e^{rt}}\), trong đó, \(A\) dân số của một vùng ( hoặc quốc gia) đó ở năm \(0\)và \(r\) là tỉ lệ tăng dân số hàng năm. Biết rằng dân số Việt Nam năm \(2021\) ước tính là \(98\,564\,407\)người và tỉ lệ tăng dân số hàng năm là \(r = 0,93\% \). Giả sử tỉ lệ tăng dân số hàng năm là như nhau tính từ năm \(2021\). Hỏi từ năm nào trở đi, dân số nước ta vượt \(120\) triệu người?
Lương tháng của 50 nhân viên một công ty được biểu diễn ở biểu đồ sau:
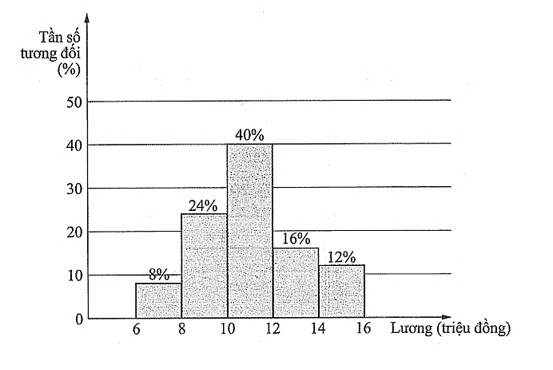
Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm trên (đơn vị: triệu đồng, làm tròn kết quả đến hàng phần trăm).
Một cái hộp hình lập phương, bên trong nó đựng một mô hình đồ chơi có dạng hình chóp tứ giác đều mà đỉnh của hình chóp đó trùng với tâm của một mặt chiếc hộp, giả sử hình vuông đáy của hình chóp trùng với một mặt của chiếc hộp (mặt này cùng với mặt chứa đỉnh hình chóp là hai mặt đối nhau). Biết cạnh của chiếc hộp bằng \(30\;{\rm{cm}}\), hãy tính thể tích phần không gian bên trong chiếc hộp không bị chiếm bởi mô hình đồ chơi dạng hình chóp (mô hình đồ hơi được làm bởi chất liệu nhựa đặc bên trong, kết quả có đơn vị là dm3).
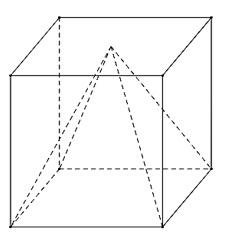
Trong không gian \(Oxyz\), cho các điểm \(A\left( {2;2;0} \right)\), \(B\left( {2;0; - 2} \right)\) và mặt phẳng \(\left( P \right):x + 2y - z - 1 = 0\). Xét điểm \(M\left( {a;b;c} \right)\) thuộc mặt phẳng \(\left( P \right)\) sao cho \(MA = MB\) và số đo góc \(\widehat {AMB}\) lớn nhất. Tính giá trị \(a + b + c\)(làm tròn kết quả đến hàng phần trăm).