Đề thi Học kì 1 Toán 10 Cánh diều có đáp án - Đề 1

Trong các câu sau, câu nào không là mệnh đề ?

Cặp số $(x;y)$ nào sau đây không là nghiệm của bất phương trình $4x-9y-3\ge 0$?

Cách viết nào sau đây là đúng?

Cho hình vẽ sau:

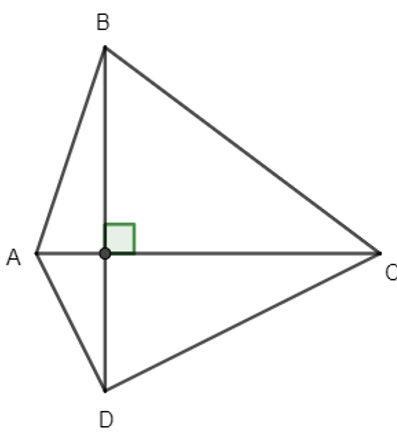
Tích vô hướng của hai vectơ nào bằng 0?

Cho hình thoi ABCD  cạnh a và $\widehat{ABD}=60°$. Độ dài vectơ $\overrightarrow{BD}$ là

Tính $\overrightarrow{AD}-\overrightarrow{AC}+\overrightarrow{DC}$                          

Với α∈ (120°; 270°) thì giá trị lượng giác nào dưới đây nhận giá trị âm?

A. sinα;

B. cosα;

C. tanα;                                                          

D. cotα.

Trong các bất phương trình sau, bất phương trình bậc nhất hai ẩn là

Cho đồ thị hàm số sau:

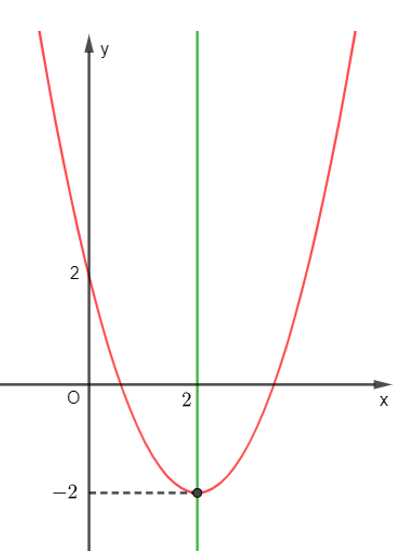
Đồ thị hàm số trên là của hàm số nào dưới đây?

Cho tam giác ABC, có G là trọng tâm tam giác, M là điểm bất kì. Biểu thức nào sau đây là đúng?

Cho đồ thị hàm số:

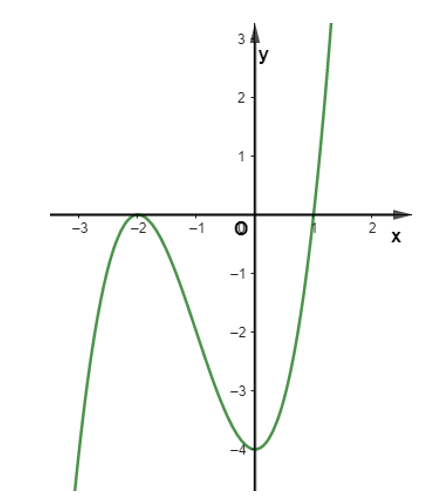
Hàm số đồng biến trên khoảng

Hàm số f(x) = x² – 2x + 1 nhận giá trị dương khi

Cặp số (0; 1) là nghiệm của hệ bất phương trình nào sau đây?

Cho hàm số y = f(x) có bảng biến thiên sau:

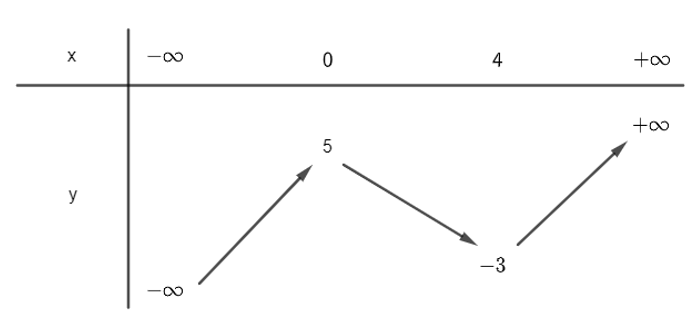
Tập giá trị của hàm số f(x) là:

Cho các bất phương trình sau:

– 2x + 1 < 0; $\frac{1}{2}{y}^2-\sqrt{2}\left(y-1\right)\le 0$; $x^2-\sqrt{x}>0$; y² + x² – 2x < 0.

Có bao nhiêu bất phương trình không là bất phương trình bậc hai một ẩn?

Hàm số bậc hai y = 2x² – $\frac{1}{3}$x có trục đối xứng là

Tập nghiệm của bất phương trình x² – 5x + 6 < 0 là

A. S = (2; 3);

B. S = (– ∞; 2);    

C. S = (3; +∞);            

D. S = (– ∞; 2) ∪ (3; +∞).

Để giải phương trình: $\sqrt{3x-1}=x^2-1$ cần điều kiện:

Lớp 10B có 45 học sinh, trong đó có 25 em thích môn Văn, 20 em thích môn Toán, 18 em thích môn Sử, 6 em không thích môn nào, 6 em thích cả Sử và Toán, 8 em thích cả Văn và Toán, 5 em thích cả ba môn. Số học sinh thích cả Văn và Sử là

Tam giác ABC có $AB=3,AC=6$ và $\widehat{A}=60°$. Bán kính R của đường tròn ngoại tiếp tam giác ABC là

Trong các công thức dưới đây, công thức nào tính diện tích tam giác ABC là đúng?

A. S_ABC = $\frac{1}{2}b.c.\cos A$;  

B. S_ABC = $\frac{abc}{4R}$;             

C. S_ABC = pR;               

D. S_ABC = a.h_a.

Tính giá trị biểu thức: cos20° + cos40° + cos60° + ... + cos160° + cos180°.

Cho hàm số $f\left(x\right)=\frac{\sqrt{2x+4}}{x-\sqrt{x}-2}$. Tập xác định D của hàm số là

Cho tam giác ABC có AB=5, BC=7, CA=8 . Tam giác ABC là

Cho tam giác ABC có M là trung điểm của AC, N là trung điểm của BC và AB = a. Độ dài vectơ $\overrightarrow{CM}-\overrightarrow{NB}$ bằng

Cho 90° <α< 180°. Xác định dấu của biểu thức M = sin(90° – α).cot(180° + α).

A. M ≥ 0;   

B. M ≤ 0;                     

C. M > 0;                     

D. M < 0.

Cho tam giác ABC đều cạnh bằng a, AH là đường cao. Tính $\overrightarrow{AB}.\overrightarrow{AH}$

Cho tứ giác ABCD, có I, J lần lượt là trung điểm của AB và CD. Ta có $\overrightarrow{\text{IJ}}=a\overrightarrow{AC}+b\overrightarrow{BD}$. Khi đó a – b bằng

Cho phương trình: $\sqrt{x^2-5x+1}=\sqrt{x-7}$. Số nghiệm của phương trình là