12 câu hỏi
Viết mệnh đề sau bằng ký hiệu và : “Mọi số thực đều có bình phương không âm”.
\(\forall x \in \mathbb{R}:{x^2} \ge 0\).
\(\exists x \in \mathbb{R}:{x^2} \ge 0\).
\(\exists x \in \mathbb{R}:{x^2} \le 0\).
\(\forall x \in \mathbb{R}:{x^2} \le 0\).
Mệnh đề phủ định của mệnh đề “9 > 4” là
\(9 < 4\).
\(9 \le 4\).
\(9 \ge 4\).
\(4 < 9\).
Cho tập hợp \(A = \left\{ {x \in \mathbb{Z}| - 1 \le x \le 4} \right\}\). Tập hợp A được viết dưới dạng liệt kê các phần tử là
\(A = \left\{ { - 1;0;1;2;3} \right\}\).
\(A = \left\{ {0;1;2;3} \right\}\).
\(A = \left\{ {0;1;2;3;4} \right\}\).
\(A = \left\{ { - 1;0;1;2;3;4} \right\}\).
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
\(x - 3{y^2} \ge 0\).
\(\left( {x - 1} \right)\left( {y + 3} \right) < x + 2\).
\(2x + 3y \ge 4\).
\(x + \frac{2}{y} < 0\).
Điểm \(M\left( {2023;1} \right)\) thuộc miền nghiệm của hệ bất phương trình nào sau đây?
\(\left\{ \begin{array}{l}x + 2y \ge 3\\3x - y \le 0\end{array} \right.\).
\(\left\{ \begin{array}{l}3x + 2y \ge 2\\x - 2y < 5\end{array} \right.\).
\(\left\{ \begin{array}{l}5x + 2y \ge 1\\3x - y \le 4\end{array} \right.\).
\(\left\{ \begin{array}{l}x - 2y > 7\\ - 2x + y \le 3\end{array} \right.\).
Cho . Khẳng định nào sau đây sai?
\(\tan \alpha > 0\).
\(\sin \alpha > 0\).
\(\cos \alpha < 0\).
\(\cot \alpha > 0\).
Cho tam giác \(ABC\) có chu vi bằng 12 và bán kính đường tròn nội tiếp bằng 1. Diện tích của tam giác \(ABC\) bằng
\(12\).
\(3\).
\(6\).
\(24\).
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương. Khẳng định nào sau đây đúng?
\(\overrightarrow a \) và \(\overrightarrow b \) có giá trùng nhau.
\(\overrightarrow a \) và \(\overrightarrow b \) có giá song song.
\(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng.
\(\overrightarrow a \) và \(\overrightarrow b \) có giá song song hoặc trùng nhau.
Cho bốn điểm phân biệt \[A,B,C,D\]. Vectơ tổng \[\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} \] bằng
\(\overrightarrow 0 \).
\(\overrightarrow {AC} \)
\(\overrightarrow {BD} \).
\(\overrightarrow {BA} \).
Mệnh đề nào sau đây sai?
Nếu một tam giác có một góc bằng 600thì tam giác đó là đều.
Tam giác \(ABC\) cân tại\(A\)\[ \Rightarrow \]\(AB = AC\).
Tổng của hai cạnh một tam giác lớn hơn cạnh thứ ba.
Tam giác \(ABC\) vuông tại \(C\)\[ \Rightarrow \]\(A{B^2} = C{A^2} + C{B^2}\).
Phần không bị gạch (kể cả bờ) trong hình vẽ là miền nghiệm của bất phương trình nào sau đây?
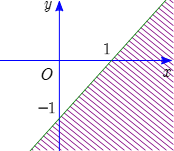
\(x - y \ge 1\).
\(x - y \le 1\).
\(x + y > 1\).
\(x + y \le 1\).
Cho biết \(\cos \alpha = - \frac{2}{3}\). Tính giá trị của biểu thức \(E = \frac{{\cot \alpha + 3\tan \alpha }}{{2\cot \alpha + \tan \alpha }}\).
\( - \frac{{19}}{{13}}\).
\(\frac{{19}}{{13}}\).
\(\frac{{25}}{{13}}\).
\( - \frac{{25}}{{13}}\).
